Spark圖計算GraphX介紹及例項
1、GraphX介紹
1.1 GraphX應用背景
Spark GraphX是一個分散式圖處理框架,它是基於Spark平臺提供對圖計算和圖挖掘簡潔易用的而豐富的介面,極大的方便了對分散式圖處理的需求。
眾所周知·,社交網路中人與人之間有很多關係鏈,例如Twitter、Facebook、微博和微信等,這些都是大資料產生的地方都需要圖計算,現在的圖處理基本都是分散式的圖處理,而並非單機處理。Spark GraphX由於底層是基於Spark來處理的,所以天然就是一個分散式的圖處理系統。
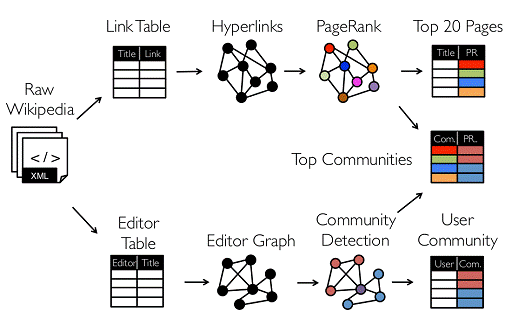
圖的分散式或者並行處理其實是把圖拆分成很多的子圖,然後分別對這些子圖進行計算,計算的時候可以分別迭代進行分階段的計算,即對圖進行平行計算。下面我們看一下圖計算的簡單示例:
從圖中我們可以看出:拿到Wikipedia的文件以後,可以變成Link Table形式的檢視,然後基於Link Table形式的檢視可以分析成Hyperlinks超連結,最後我們可以使用PageRank去分析得出Top Communities。在下面路徑中的Editor Graph到Community,這個過程可以稱之為Triangle Computation,這是計算三角形的一個演算法,基於此會發現一個社群。從上面的分析中我們可以發現圖計算有很多的做法和演算法,同時也發現圖和表格可以做互相的轉換。
1.2 GraphX的框架
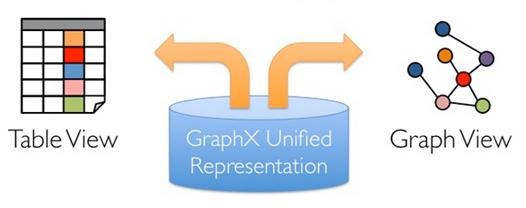
設計GraphX時,點分割和GAS都已成熟,在設計和編碼中針對它們進行了優化,並在功能和效能之間尋找最佳的平衡點。如同Spark本身,每個子模組都有一個核心抽象。GraphX的核心抽象是Resilient Distributed Property Graph,一種點和邊都帶屬性的有向多重圖。它擴充套件了Spark RDD的抽象,有Table和Graph兩種檢視,而只需要一份物理儲存。兩種檢視都有自己獨有的操作符,從而獲得了靈活操作和執行效率。
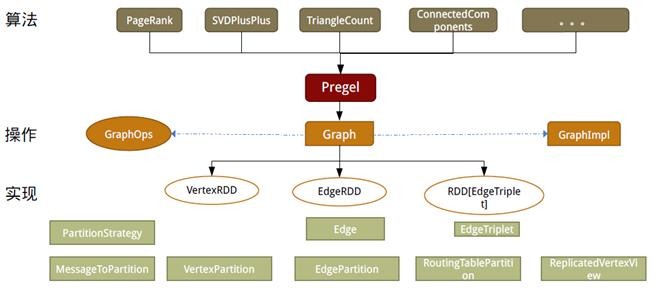
如同Spark,GraphX的程式碼非常簡潔。GraphX的核心程式碼只有3千多行,而在此之上實現的Pregel模式,只要短短的20多行。GraphX的程式碼結構整體下圖所示,其中大部分的實現,都是圍繞Partition的優化進行的。這在某種程度上說明了點分割的儲存和相應的計算優化,的確是圖計算框架的重點和難點。
1.3 發展歷程
l早在0.5版本,Spark就帶了一個小型的Bagel模組,提供了類似Pregel的功能。當然,這個版本還非常原始,效能和功能都比較弱,屬於實驗型產品。
l到0.8版本時,鑑於業界對分散式圖計算的需求日益見漲,Spark開始獨立一個分支Graphx-Branch,作為獨立的圖計算模組,借鑑GraphLab,開始設計開發GraphX。
l在0.9版本中,這個模組被正式整合到主幹,雖然是Alpha版本,但已可以試用,小麵包圈Bagel告別舞臺。1.0版本,GraphX正式投入生產使用。
值得注意的是,GraphX目前依然處於快速發展中,從0.8的分支到0.9和1.0,每個版本程式碼都有不少的改進和重構。根據觀察,在沒有改任何程式碼邏輯和執行環境,只是升級版本、切換介面和重新編譯的情況下,每個版本有10%~20%的效能提升。雖然和GraphLab的效能還有一定差距,但憑藉Spark整體上的一體化流水線處理,社群熱烈的活躍度及快速改進速度,GraphX具有強大的競爭力。
2、GraphX實現分析
如同Spark本身,每個子模組都有一個核心抽象。GraphX的核心抽象是Resilient Distributed Property Graph,一種點和邊都帶屬性的有向多重圖。它擴充套件了Spark RDD的抽象,有Table和Graph兩種檢視,而只需要一份物理儲存。兩種檢視都有自己獨有的操作符,從而獲得了靈活操作和執行效率。
GraphX的底層設計有以下幾個關鍵點。
對Graph檢視的所有操作,最終都會轉換成其關聯的Table檢視的RDD操作來完成。這樣對一個圖的計算,最終在邏輯上,等價於一系列RDD的轉換過程。因此,Graph最終具備了RDD的3個關鍵特性:Immutable、Distributed和Fault-Tolerant,其中最關鍵的是Immutable(不變性)。邏輯上,所有圖的轉換和操作都產生了一個新圖;物理上,GraphX會有一定程度的不變頂點和邊的複用優化,對使用者透明。
兩種檢視底層共用的物理資料,由RDD[Vertex-Partition]和RDD[EdgePartition]這兩個RDD組成。點和邊實際都不是以表Collection[tuple]的形式儲存的,而是由VertexPartition/EdgePartition在內部儲存一個帶索引結構的分片資料塊,以加速不同檢視下的遍歷速度。不變的索引結構在RDD轉換過程中是共用的,降低了計算和儲存開銷。
圖的分散式儲存採用點分割模式,而且使用partitionBy方法,由使用者指定不同的劃分策略(PartitionStrategy)。劃分策略會將邊分配到各個EdgePartition,頂點Master分配到各個VertexPartition,EdgePartition也會快取本地邊關聯點的Ghost副本。劃分策略的不同會影響到所需要快取的Ghost副本數量,以及每個EdgePartition分配的邊的均衡程度,需要根據圖的結構特徵選取最佳策略。目前有EdgePartition2d、EdgePartition1d、RandomVertexCut和CanonicalRandomVertexCut這四種策略。
2.1 儲存模式
2.1.1 圖儲存模式
巨型圖的儲存總體上有邊分割和點分割兩種儲存方式。2013年,GraphLab2.0將其儲存方式由邊分割變為點分割,在效能上取得重大提升,目前基本上被業界廣泛接受並使用。
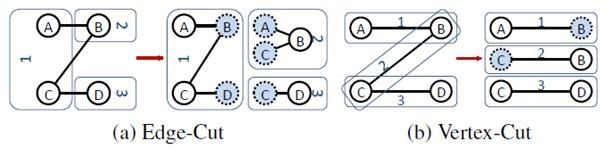
l邊分割(Edge-Cut):每個頂點都儲存一次,但有的邊會被打斷分到兩臺機器上。這樣做的好處是節省儲存空間;壞處是對圖進行基於邊的計算時,對於一條兩個頂點被分到不同機器上的邊來說,要跨機器通訊傳輸資料,內網通訊流量大。
l點分割(Vertex-Cut):每條邊只儲存一次,都只會出現在一臺機器上。鄰居多的點會被複制到多臺機器上,增加了儲存開銷,同時會引發資料同步問題。好處是可以大幅減少內網通訊量。
雖然兩種方法互有利弊,但現在是點分割佔上風,各種分散式圖計算框架都將自己底層的儲存形式變成了點分割。主要原因有以下兩個。
1.磁碟價格下降,儲存空間不再是問題,而內網的通訊資源沒有突破性進展,叢集計算時內網頻寬是寶貴的,時間比磁碟更珍貴。這點就類似於常見的空間換時間的策略。
2.在當前的應用場景中,絕大多數網路都是“無尺度網路”,遵循冪律分佈,不同點的鄰居數量相差非常懸殊。而邊分割會使那些多鄰居的點所相連的邊大多數被分到不同的機器上,這樣的資料分佈會使得內網頻寬更加捉襟見肘,於是邊分割儲存方式被漸漸拋棄了。
2.1.2 GraphX儲存模式
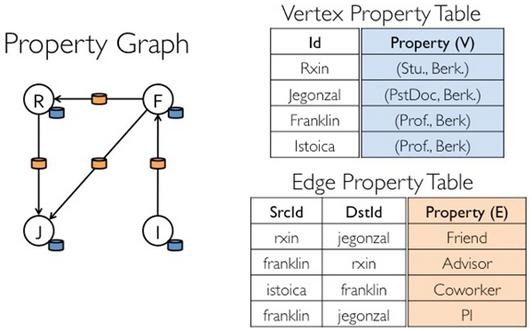
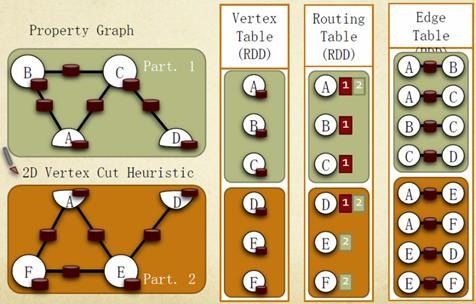
Graphx借鑑PowerGraph,使用的是Vertex-Cut(點分割)方式儲存圖,用三個RDD儲存圖資料資訊:
lVertexTable(id, data):id為Vertex id,data為Edge data
lEdgeTable(pid, src, dst, data):pid為Partion id,src為原定點id,dst為目的頂點id
lRoutingTable(id, pid):id為Vertex id,pid為Partion id
點分割儲存實現如下圖所示:
2.2 計算模式
2.2.1 圖計算模式
目前基於圖的平行計算框架已經有很多,比如來自Google的Pregel、來自Apache開源的圖計算框架Giraph/HAMA以及最為著名的GraphLab,其中Pregel、HAMA和Giraph都是非常類似的,都是基於BSP(Bulk Synchronous Parallell)模式。
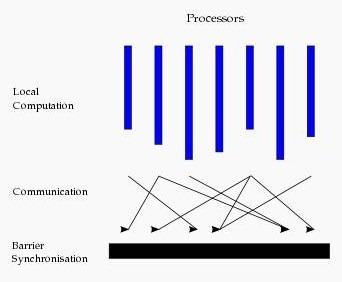
Bulk Synchronous Parallell,即整體同步並行,它將計算分成一系列的超步(superstep)的迭代(iteration)。從縱向上看,它是一個序列模式,而從橫向上看,它是一個並行的模式,每兩個superstep之間設定一個柵欄(barrier),即整體同步點,確定所有並行的計算都完成後再啟動下一輪superstep。
每一個超步(superstep)包含三部分內容:
1.計算compute:每一個processor利用上一個superstep傳過來的訊息和本地的資料進行本地計算;
2.訊息傳遞:每一個processor計算完畢後,將訊息傳遞個與之關聯的其它processors
3.整體同步點:用於整體同步,確定所有的計算和訊息傳遞都進行完畢後,進入下一個superstep。
2.2.2GraphX計算模式
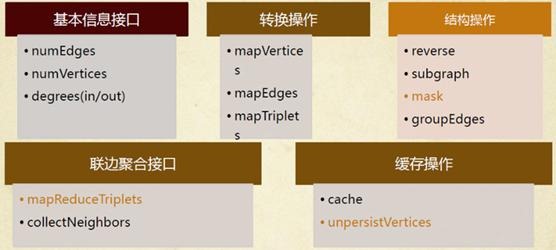
如同Spark一樣,GraphX的Graph類提供了豐富的圖運算子,大致結構如下圖所示。可以在官方GraphX Programming Guide中找到每個函式的詳細說明,本文僅講述幾個需要注意的方法。
2.2.2.1 圖的快取
每個圖是由3個RDD組成,所以會佔用更多的記憶體。相應圖的cache、unpersist和checkpoint,更需要注意使用技巧。出於最大限度複用邊的理念,GraphX的預設介面只提供了unpersistVertices方法。如果要釋放邊,呼叫g.edges.unpersist()方法才行,這給使用者帶來了一定的不便,但為GraphX的優化提供了便利和空間。參考GraphX的Pregel程式碼,對一個大圖,目前最佳的實踐是:
大體之意是根據GraphX中Graph的不變性,對g做操作並賦回給g之後,g已不是原來的g了,而且會在下一輪迭代使用,所以必須cache。另外,必須先用prevG保留住對原來圖的引用,並在新圖產生後,快速將舊圖徹底釋放掉。否則,十幾輪迭代後,會有記憶體洩漏問題,很快耗光作業快取空間。
2.2.2.2 鄰邊聚合
mrTriplets(mapReduceTriplets)是GraphX中最核心的一個介面。Pregel也基於它而來,所以對它的優化能很大程度上影響整個GraphX的效能。mrTriplets運算子的簡化定義是:
它的計算過程為:map,應用於每一個Triplet上,生成一個或者多個訊息,訊息以Triplet關聯的兩個頂點中的任意一個或兩個為目標頂點;reduce,應用於每一個Vertex上,將傳送給每一個頂點的訊息合併起來。
mrTriplets最後返回的是一個VertexRDD[A],包含每一個頂點聚合之後的訊息(型別為A),沒有接收到訊息的頂點不會包含在返回的VertexRDD中。
在最近的版本中,GraphX針對它進行了一些優化,對於Pregel以及所有上層演算法工具包的效能都有重大影響。主要包括以下幾點。
1. Caching for Iterative mrTriplets & Incremental Updates for Iterative mrTriplets:在很多圖分析演算法中,不同點的收斂速度變化很大。在迭代後期,只有很少的點會有更新。因此,對於沒有更新的點,下一次mrTriplets計算時EdgeRDD無需更新相應點值的本地快取,大幅降低了通訊開銷。
2.Indexing Active Edges:沒有更新的頂點在下一輪迭代時不需要向鄰居重新發送訊息。因此,mrTriplets遍歷邊時,如果一條邊的鄰居點值在上一輪迭代時沒有更新,則直接跳過,避免了大量無用的計算和通訊。
3.Join Elimination:Triplet是由一條邊和其兩個鄰居點組成的三元組,操作Triplet的map函式常常只需訪問其兩個鄰居點值中的一個。例如,在PageRank計算中,一個點值的更新只與其源頂點的值有關,而與其所指向的目的頂點的值無關。那麼在mrTriplets計算中,就不需要VertexRDD和EdgeRDD的3-way join,而只需要2-way join。
所有這些優化使GraphX的效能逐漸逼近GraphLab。雖然還有一定差距,但一體化的流水線服務和豐富的程式設計介面,可以彌補效能的微小差距。
2.2.2.3 進化的Pregel模式
GraphX中的Pregel介面,並不嚴格遵循Pregel模式,它是一個參考GAS改進的Pregel模式。定義如下:
這種基於mrTrilets方法的Pregel模式,與標準Pregel的最大區別是,它的第2段引數體接收的是3個函式引數,而不接收messageList。它不會在單個頂點上進行訊息遍歷,而是將頂點的多個Ghost副本收到的訊息聚合後,傳送給Master副本,再使用vprog函式來更新點值。訊息的接收和傳送都被自動並行化處理,無需擔心超級節點的問題。
常見的程式碼模板如下所示:
可以看到,GraphX設計這個模式的用意。它綜合了Pregel和GAS兩者的優點,即介面相對簡單,又保證效能,可以應對點分割的圖儲存模式,勝任符合冪律分佈的自然圖的大型計算。另外,值得注意的是,官方的Pregel版本是最簡單的一個版本。對於複雜的業務場景,根據這個版本擴充套件一個定製的Pregel是很常見的做法。
2.2.2.4 圖演算法工具包
GraphX也提供了一套圖演算法工具包,方便使用者對圖進行分析。目前最新版本已支援PageRank、數三角形、最大連通圖和最短路徑等6種經典的圖演算法。這些演算法的程式碼實現,目的和重點在於通用性。如果要獲得最佳效能,可以參考其實現進行修改和擴充套件滿足業務需求。另外,研讀這些程式碼,也是理解GraphX程式設計最佳實踐的好方法。
3、GraphX例項
3.1 圖例演示
3.1.1 例子介紹
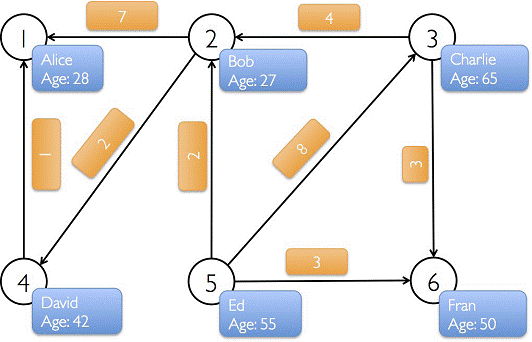
下圖中有6個人,每個人有名字和年齡,這些人根據社會關係形成8條邊,每條邊有其屬性。在以下例子演示中將構建頂點、邊和圖,列印圖的屬性、轉換操作、結構操作、連線操作、聚合操作,並結合實際要求進行演示。
3.1.2 程式程式碼
import org.apache.log4j.{Level, Logger}
import org.apache.spark.{SparkContext, SparkConf}
import org.apache.spark.graphx._
import org.apache.spark.rdd.RDD
object GraphXExample {
def main(args: Array[String]) {
//遮蔽日誌
Logger.getLogger("org.apache.spark").setLevel(Level.WARN)
Logger.getLogger("org.eclipse.jetty.server").setLevel(Level.OFF)
//設定執行環境
val conf = new SparkConf().setAppName("SimpleGraphX").setMaster("local")
val sc = new SparkContext(conf)
//設定頂點和邊,注意頂點和邊都是用元組定義的Array
//頂點的資料型別是VD:(String,Int)
val vertexArray = Array(
(1L, ("Alice", 28)),
(2L, ("Bob", 27)),
(3L, ("Charlie", 65)),
(4L, ("David", 42)),
(5L, ("Ed", 55)),
(6L, ("Fran", 50))
)
//邊的資料型別ED:Int
val edgeArray = Array(
Edge(2L, 1L, 7),
Edge(2L, 4L, 2),
Edge(3L, 2L, 4),
Edge(3L, 6L, 3),
Edge(4L, 1L, 1),
Edge(5L, 2L, 2),
Edge(5L, 3L, 8),
Edge(5L, 6L, 3)
)
//構造vertexRDD和edgeRDD
val vertexRDD: RDD[(Long, (String, Int))] = sc.parallelize(vertexArray)
val edgeRDD: RDD[Edge[Int]] = sc.parallelize(edgeArray)
//構造圖Graph[VD,ED]
val graph: Graph[(String, Int), Int] = Graph(vertexRDD, edgeRDD)
//***********************************************************************************
//*************************** 圖的屬性 ****************************************
//********************************************************************************** println("***********************************************")
println("屬性演示")
println("**********************************************************")
println("找出圖中年齡大於30的頂點:")
graph.vertices.filter { case (id, (name, age)) => age > 30}.collect.foreach {
case (id, (name, age)) => println(s"$name is $age")
}
//邊操作:找出圖中屬性大於5的邊
println("找出圖中屬性大於5的邊:")
graph.edges.filter(e => e.attr > 5).collect.foreach(e => println(s"${e.srcId} to ${e.dstId} att ${e.attr}"))
println
//triplets操作,((srcId, srcAttr), (dstId, dstAttr), attr)
println("列出邊屬性>5的tripltes:")
for (triplet <- graph.triplets.filter(t => t.attr > 5).collect) {
println(s"${triplet.srcAttr._1} likes ${triplet.dstAttr._1}")
}
println
//Degrees操作
println("找出圖中最大的出度、入度、度數:")
def max(a: (VertexId, Int), b: (VertexId, Int)): (VertexId, Int) = {
if (a._2 > b._2) a else b
}
println("max of outDegrees:" + graph.outDegrees.reduce(max) + " max of inDegrees:" + graph.inDegrees.reduce(max) + " max of Degrees:" + graph.degrees.reduce(max))
println
//***********************************************************************************
//*************************** 轉換操作 ****************************************
//**********************************************************************************
println("**********************************************************")
println("轉換操作")
println("**********************************************************")
println("頂點的轉換操作,頂點age + 10:")
graph.mapVertices{ case (id, (name, age)) => (id, (name, age+10))}.vertices.collect.foreach(v => println(s"${v._2._1} is ${v._2._2}"))
println
println("邊的轉換操作,邊的屬性*2:")
graph.mapEdges(e=>e.attr*2).edges.collect.foreach(e => println(s"${e.srcId} to ${e.dstId} att ${e.attr}"))
println
//***********************************************************************************
//*************************** 結構操作 ****************************************
//**********************************************************************************
println("**********************************************************")
println("結構操作")
println("**********************************************************")
println("頂點年紀>30的子圖:")
val subGraph = graph.subgraph(vpred = (id, vd) => vd._2 >= 30)
println("子圖所有頂點:")
subGraph.vertices.collect.foreach(v => println(s"${v._2._1} is ${v._2._2}"))
println
println("子圖所有邊:")
subGraph.edges.collect.foreach(e => println(s"${e.srcId} to ${e.dstId} att ${e.attr}"))
println
//***********************************************************************************
//*************************** 連線操作 ****************************************
//**********************************************************************************
println("**********************************************************")
println("連線操作")
println("**********************************************************")
val inDegrees: VertexRDD[Int] = graph.inDegrees
case class User(name: String, age: Int, inDeg: Int, outDeg: Int)
//建立一個新圖,頂點VD的資料型別為User,並從graph做型別轉換
val initialUserGraph: Graph[User, Int] = graph.mapVertices { case (id, (name, age)) => User(name, age, 0, 0)}
//initialUserGraph與inDegrees、outDegrees(RDD)進行連線,並修改initialUserGraph中inDeg值、outDeg值
val userGraph = initialUserGraph.outerJoinVertices(initialUserGraph.inDegrees) {
case (id, u, inDegOpt) => User(u.name, u.age, inDegOpt.getOrElse(0), u.outDeg)
}.outerJoinVertices(initialUserGraph.outDegrees) {
case (id, u, outDegOpt) => User(u.name, u.age, u.inDeg,outDegOpt.getOrElse(0))
}
println("連線圖的屬性:")
userGraph.vertices.collect.foreach(v => println(s"${v._2.name} inDeg: ${v._2.inDeg} outDeg: ${v._2.outDeg}"))
println
println("出度和入讀相同的人員:")
userGraph.vertices.filter {
case (id, u) => u.inDeg == u.outDeg
}.collect.foreach {
case (id, property) => println(property.name)
}
println
//***********************************************************************************
//*************************** 聚合操作 ****************************************
//**********************************************************************************
println("**********************************************************")
println("聚合操作")
println("**********************************************************")
println("找出年紀最大的追求者:")
val oldestFollower: VertexRDD[(String, Int)] = userGraph.mapReduceTriplets[(String, Int)](
// 將源頂點的屬性發送給目標頂點,map過程
edge => Iterator((edge.dstId, (edge.srcAttr.name, edge.srcAttr.age))),
// 得到最大追求者,reduce過程
(a, b) => if (a._2 > b._2) a else b
)
userGraph.vertices.leftJoin(oldestFollower) { (id, user, optOldestFollower) =>
optOldestFollower match {
case None => s"${user.name} does not have any followers."
case Some((name, age)) => s"${name} is the oldest follower of ${user.name}."
}
}.collect.foreach { case (id, str) => println(str)}
println
//***********************************************************************************
//*************************** 實用操作 ****************************************
//**********************************************************************************
println("**********************************************************")
println("聚合操作")
println("**********************************************************")
println("找出5到各頂點的最短:")
val sourceId: VertexId = 5L // 定義源點
val initialGraph = graph.mapVertices((id, _) => if (id == sourceId) 0.0 else Double.PositiveInfinity)
val sssp = initialGraph.pregel(Double.PositiveInfinity)(
(id, dist, newDist) => math.min(dist, newDist),
triplet => { // 計算權重
if (triplet.srcAttr + triplet.attr < triplet.dstAttr) {
Iterator((triplet.dstId, triplet.srcAttr + triplet.attr))
} else {
Iterator.empty
}
},
(a,b) => math.min(a,b) // 最短距離
)
println(sssp.vertices.collect.mkString("\n"))
sc.stop()
}
}
3.1.3 執行結果
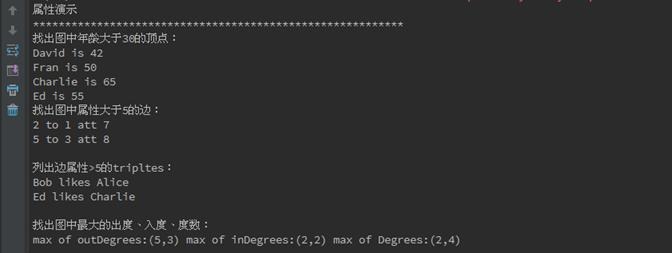
在IDEA(如何使用IDEA參見第3課《3.Spark程式設計模型(下)--IDEA搭建及實戰》)中首先對GraphXExample.scala程式碼進行編譯,編譯通過後進行執行,執行結果如下:
**********************************************************
屬性演示
**********************************************************
找出圖中年齡大於30的頂點:
David is 42
Fran is 50
Charlie is 65
Ed is 55
找出圖中屬性大於5的邊:
2 to 1 att 7
5 to 3 att 8
列出邊屬性>5的tripltes:
Bob likes Alice
Ed likes Charlie
找出圖中最大的出度、入度、度數:
max of outDegrees:(5,3) max of inDegrees:(2,2) max of Degrees:(2,4)
**********************************************************
轉換操作
**********************************************************
頂點的轉換操作,頂點age + 10:
4 is (David,52)
1 is (Alice,38)
6 is (Fran,60)
3 is (Charlie,75)
5 is (Ed,65)
2 is (Bob,37)
邊的轉換操作,邊的屬性*2:
2 to 1 att 14
2 to 4 att 4
3 to 2 att 8
3 to 6 att 6
4 to 1 att 2
5 to 2 att 4
5 to 3 att 16
5 to 6 att 6
**********************************************************
結構操作
**********************************************************
頂點年紀>30的子圖:
子圖所有頂點:
David is 42
Fran is 50
Charlie is 65
Ed is 55
子圖所有邊:
3 to 6 att 3
5 to 3 att 8
5 to 6 att 3
**********************************************************
連線操作
**********************************************************
連線圖的屬性:
David inDeg: 1 outDeg: 1
Alice inDeg: 2 outDeg: 0
Fran inDeg: 2 outDeg: 0
Charlie inDeg: 1 outDeg: 2
Ed inDeg: 0 outDeg: 3
Bob inDeg: 2 outDeg: 2
出度和入讀相同的人員:
David
Bob
**********************************************************
聚合操作
**********************************************************
找出年紀最大的追求者:
Bob is the oldest follower of David.
David is the oldest follower of Alice.
Charlie is the oldest follower of Fran.
Ed is the oldest follower of Charlie.
Ed does not have any followers.
Charlie is the oldest follower of Bob.
**********************************************************
實用操作
**********************************************************
找出5到各頂點的最短:
(4,4.0)
(1,5.0)
(6,3.0)
(3,8.0)
(5,0.0)
(2,2.0)
3.2 PageRank 演示
3.2.1 例子介紹
PageRank, 即網頁排名,又稱網頁級別、Google 左側排名或佩奇排名。它是Google 創始人拉里· 佩奇和謝爾蓋· 布林於1997 年構建早期的搜尋系統原型時提出的連結分析演算法。目前很多重要的連結分析演算法都是在PageRank 演算法基礎上衍生出來的。PageRank 是Google 用於用來標識網頁的等級/ 重要性的一種方法,是Google 用來衡量一個網站的好壞的唯一標準。在揉合了諸如Title 標識和Keywords 標識等所有其它因素之後,Google 通過PageRank 來調整結果,使那些更具“等級/ 重要性”的網頁在搜尋結果中令網站排名獲得提升,從而提高搜尋結果的相關性和質量。
3.2.2 測試資料
在這裡測試資料為頂點資料graphx-wiki-vertices.txt和邊資料graphx-wiki-edges.txt,可以在本系列附帶資源/data/class9/目錄中找到這兩個資料檔案,其中格式為:
l 頂點為頂點編號和網頁標題
l 邊資料由兩個頂點構成
3.2.3 程式程式碼
import org.apache.log4j.{Level, Logger}
import org.apache.spark.{SparkContext, SparkConf}
import org.apache.spark.graphx._
import org.apache.spark.rdd.RDD
object PageRank {
def main(args: Array[String]) {
//遮蔽日誌
Logger.getLogger("org.apache.spark").setLevel(Level.WARN)
Logger.getLogger("org.eclipse.jetty.server").setLevel(Level.OFF)
//設定執行環境
val conf = new SparkConf().setAppName("PageRank").setMaster("local")
val sc = new SparkContext(conf)
//讀入資料檔案
val articles: RDD[String] = sc.textFile("/home/hadoop/IdeaProjects/data/graphx/graphx-wiki-vertices.txt")
val links: RDD[String] = sc.textFile("/home/hadoop/IdeaProjects/data/graphx/graphx-wiki-edges.txt")
//裝載頂點和邊
val vertices = articles.map { line =>
val fields = line.split('\t')
(fields(0).toLong, fields(1))
}
val edges = links.map { line =>
val fields = line.split('\t')
Edge(fields(0).toLong, fields(1).toLong, 0)
}
//cache操作
//val graph = Graph(vertices, edges, "").persist(StorageLevel.MEMORY_ONLY_SER)
val graph = Graph(vertices, edges, "").persist()
//graph.unpersistVertices(false)
//測試
println("**********************************************************")
println("獲取5個triplet資訊")
println("**********************************************************")
graph.triplets.take(5).foreach(println(_))
//pageRank演算法裡面的時候使用了cache(),故前面persist的時候只能使用MEMORY_ONLY
println("**********************************************************")
println("PageRank計算,獲取最有價值的資料")
println("**********************************************************")
val prGraph = graph.pageRank(0.001).cache()
val titleAndPrGraph = graph.outerJoinVertices(prGraph.vertices) {
(v, title, rank) => (rank.getOrElse(0.0), title)
}
titleAndPrGraph.vertices.top(10) {
Ordering.by((entry: (VertexId, (Double, String))) => entry._2._1)
}.foreach(t => println(t._2._2 + ": " + t._2._1))
sc.stop()
}
}
3.2.4 執行結果
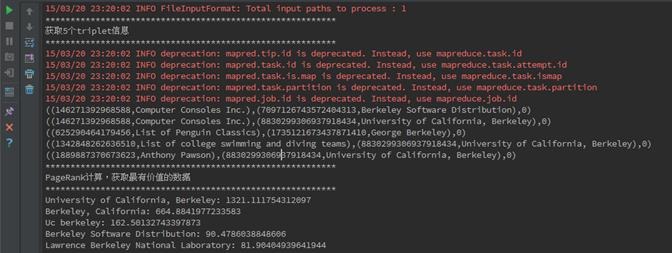
在IDEA中首先對PageRank.scala程式碼進行編譯,編譯通過後進行執行,執行結果如下:
**********************************************************
獲取5個triplet資訊
**********************************************************
((146271392968588,Computer Consoles Inc.),(7097126743572404313,Berkeley Software Distribution),0)
((146271392968588,Computer Consoles Inc.),(8830299306937918434,University of California, Berkeley),0)
((625290464179456,List of Penguin Classics),(1735121673437871410,George Berkeley),0)
((1342848262636510,List of college swimming and diving teams),(8830299306937918434,University of California, Berkeley),0)
((1889887370673623,Anthony Pawson),(8830299306937918434,University of California, Berkeley),0)
**********************************************************
PageRank計算,獲取最有價值的資料
**********************************************************
University of California, Berkeley: 1321.111754312097
Berkeley, California: 664.8841977233583
Uc berkeley: 162.50132743397873
Berkeley Software Distribution: 90.4786038848606
Lawrence Berkeley National Laboratory: 81.90404939641944
George Berkeley: 81.85226118457985
Busby Berkeley: 47.871998218019655
Berkeley Hills: 44.76406979519754
Xander Berkeley: 30.324075347288037
Berkeley County, South Carolina: 28.908336483710308
4、參考資料
(1)《GraphX:基於Spark的彈性分散式圖計算系統》 http://lidrema.blog.163.com/blog/static/20970214820147199643788/
(2)《快刀初試:Spark GraphX在淘寶的實踐》 http://www.csdn.net/article/2014-08-07/2821097