經典演算法值n後問題，

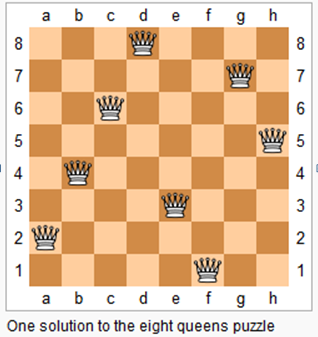
這題題給你一個n*n的棋盤，問你放置n個皇后共有多少種不用的放置方法，

在任意一個皇后所在位置的水平、豎直、以及45度斜線上都不能出現皇后的棋子

這是一個典型的回溯法框架，並且也是很簡單的一個回溯法框架，比這個更簡單的就只有字串全排列問題了。

這題使用深度優先遍歷的回溯法解決，每一行只放一個皇后，每一列只放一個皇后，如何判斷某個皇后是否和前面已經放置的皇后斜線衝突呢，使用abs(a-b)==abs(c-d)，ac,bd分別為參與判斷的兩個皇后的橫縱座標，只要這個等式成立則這兩個皇后一定斜線衝突

使用一個數組儲存，陣列的下標表示行數，陣列儲存的值表示列數，通過交換陣列每個值的位置就能實現n皇后問題的全排列的尋找

n皇后問題簡單易懂演算法框架：

大體思路是對於陣列list的第t個位置，表示第t層，其值表示這一行的皇后所在的列數，這裡假設取list[t]為這一行的列數，當取定這一行的列數後把list[t]和list[a]交換位置，那麼t+1~n（n為list長度）就是表示下一層皇后可供選擇的列數

如何判斷list[a]是否可取呢，只需要判斷llist[a]和前面已經確定的皇后位置是否斜線衝突就行了，也就是abs(a-b)==abs(c-d)，ac,bd分別為參與判斷的兩個皇后的橫縱座標

public:
bool check(vector<int> list, int t)
{
      for(int i = 0; i < t; i++)
      {
            if(abs(i - t) == abs(list[i] - list[t])) return false;
      }
      returntrue;
}
void p(vector<int> list, int t,int& count)
{
      if(t == list.size()) {
            count++;return; }
      for(int i = t; i < list.size(); i++)
      {
            swap(list[i],list[t]);
            if(check(list, t)) p(list, t+1, count);
            swap(list[i],list[t]);
      }
}
int totalNQueens(int n) {
      vector<int>list(n, 0); int count = 0;
      for(int i = 0; i < list.size(); list[i] = i,i++);
      p(list,0, count);
      returncount;
}
};
 

下面是n皇后問題的最高效率演算法：

基本思路跟上面那一個很想，不同的地方是當確定一個皇后的位置後，假設確定位置為t，則將位置t行列之和對應的flag位置設定為1，將t行列之差對應的flag位置設定為1，將t列數相同的flag設定為1，之後再找皇后的時候只需要判斷flag[i]&& !flag[row + i +n] && !flag[4* n + row - i])就行了，flag[4*n +row - i])前面加上一個4*n是因為行列之和最大為4*n

class Solution {
public:
      inttotalNQueens(int n) {
            boolflag[5 * n] ={ false };
            int num= 0;
            dfs(num, flag, 0, n);
            returnnum;
      }
      void dfs(int& num, bool* flag, int row, int n) {
            if (row == n) {
                  ++num;
                  return;
            }
            for (int i = 0; i<n; i++) {
                  if(!flag[i]&& !flag[row + i + n] && !flag[4 * n + row - i]) {
                       flag[i] = 1;
                       flag[row + i + n] = 1;
                       flag[4 * n + row - i] = 1;
                       dfs(num, flag, row + 1, n);
                       flag[i] = 0;
                       flag[row + i + n] = 0;
                       flag[4 * n + row - i] = 0;
                  }
            }
      }
};