Diffie-Hellman(迪菲-赫爾曼)祕鑰交換
Diffie-Hellman演算法是Whitefield Diffie和Martin Hellman在1976年公佈的一種祕鑰交換演算法,它是一種建立祕鑰的方法,而不是加密方法,所以祕鑰必須和其他一種加密演算法結合使用。這種祕鑰交換技術的目的在於使兩個使用者安全的交換一個祕鑰一遍後面的報文加密。
Diffie-Hellman金鑰交換演算法的有效性依賴於計算離散對數的難度。簡言之,可以如下定義離散對數:首先定義一個素數p的原根,為其各次冪產生從1 到p-1的所有整數根,也就是說,如果a是素數p的一個原根,那麼數值
a mod p, a2 mod p,…,ap-1
是各不相同的整數,並且以某種排列方式組成了從1到p-1的所有整數。
對於一個整數b和素數p的一個原根a,可以找到惟一的指數i,使得
b=ai mod p, 0<=i<=p-1
指數i稱為b的以a為基數的模p的離散對數或者指數。該值被記為inda ,p(b)。
基於此背景知識,可以定義Diffie-Hellman金鑰交換演算法。該演算法描述如下:
1、有兩個全域性公開的引數,一個素數q和一個整數a,a是q的一個原根。
2、假設使用者A和B希望交換一個金鑰,使用者A選擇一個作為私有金鑰的隨機數XA<q,並計算公開金鑰YA=a^XA mod q。A對XA的值保密存放而使YA能被B公開獲得。類似地,使用者B選擇一個私有的隨機數XB<q,並計算公開金鑰YB=a^XB mod q。B對XB的值保密存放而使YB能被A公開獲得。
3、使用者A產生共享祕密金鑰的計算方式是K = (YB)^XA mod q。同樣,使用者B產生共享祕密金鑰的計算是K = (YA)^XB mod q。這兩個計算產生相同的結果:
K = (YB)XA modq
= (aXB modq)XA mod q
= (aXB)XA modq(根據取模運算規則得到)
= aXBXA modq
= (aXA)XB modq
= (aXA modq)XB mod q
= (YA)XB modq
所以
(YB
因此相當於雙方已經交換了一個相同的祕密金鑰。
4、因為XA和XB是保密的,一個敵對方可以利用的引數只有q、a、YA和YB。因而敵對方被迫取離散對數來確定金鑰。例如,要獲取使用者B的祕密金鑰,敵對方必須先計算
XB = inda ,q(YB)
然後再使用使用者B採用的同樣方法計算其祕密金鑰K。
Diffie-Hellman金鑰交換演算法的安全性依賴於這樣一個事實:雖然計算以一個素數為模的指數相對容易,但計算離散對數卻很困難。對於大的素數,計算出離散對數幾乎是不可能的。
下面給出例子。金鑰交換基於素數q = 97和97的一個原根a = 5。A和B分別選擇私有金鑰XA = 36和XB = 58。每人計算其公開金鑰
YA = 536 = 50 mod 97
YB = 558 = 44 mod 97
在他們相互獲取了公開金鑰之後,各自通過計算得到雙方共享的祕密金鑰如下:
K = (YB)XA mod 97 = 4436 = 75 mod 97
K = (YA)XB mod 97 = 5058 = 75 mod 97
從|50,44|出發,攻擊者要計算出75很不容易。
當然,為了使這個例子變得安全,必須使用非常大的XA, XB 以及p, 否則可以實驗所有的可能取值。(總共有最多97個這樣的值, 就算XA和XB很大也無濟於事)。
如果 p 是一個至少 300 位的質數,並且XA和XB至少有100位長, 那麼即使使用全人類所有的計算資源和當今最好的演算法也不可能從a, p和a^(XA*XB) mod p 中計算出 XA*XB。
這個問題就是著名的離散對數問題。注意g則不需要很大, 並且在一般的實踐中通常是2或者5
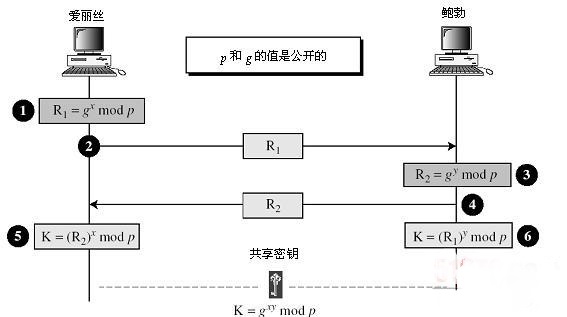
假設使用者A希望與使用者B建立一個連線,並用一個共享的祕密金鑰加密在該連線上傳輸的報文。
1.使用者A產生一個一次性的私有金鑰x,並計算出公開金鑰R1並將其傳送給使用者B。
2.使用者B產生一個私有金鑰y,計算出公開金鑰R2並將它傳送給使用者A作為響應。必要的公開數值q和a都需要提前知道。另一種方法是使用者A選擇q和a的值,並將這些數值包含在第一個報文中。
3.A使用者將接收到的R2||x||p 計算出祕鑰K,B使用者將接收到的R1||y||p 也計算出祕鑰K,這相當於A和B交換了祕鑰K。
下面再舉一個使用Diffie-Hellman演算法的例子。假設有一組使用者(例如一個區域網上的所有使用者),每個人都產生一個長期的私有金鑰XA,並計算一個公開金鑰YA。這些公開金鑰數值,連同全域性公開數值q和a都儲存在某個中央目錄中。在任何時刻,使用者B都可以訪問使用者A 的公開數值,計算一個祕密金鑰,並使用這個金鑰傳送一個加密報文給A。如果中央目錄是可信任的,那麼這種形式的通訊就提供了保密性和一定程度的鑑別功能。因為只有A和B可以確定這個金鑰,其它使用者都無法解讀報文(保密性)。接收方A知道只有使用者B才能使用此金鑰生成這個報文(鑑別)。
當然還有其他型別的祕鑰交換結構,比如無線路由器中的802.1x Enrollee --- AP --- registrar可能會使用到兩個祕鑰K1,K2:
Diffie-Hellman演算法具有兩個吸引力的特徵:
1、僅當需要時才生成金鑰,減小了將金鑰儲存很長一段時間而致使遭受攻擊的機會。
2、除對全域性引數的約定外,金鑰交換不需要事先存在的基礎結構。
然而,該技術也存在許多不足:
1、沒有提供雙方身份的任何資訊。
2、它是計算密集性的,因此容易遭受阻塞性攻擊,即對手請求大量的金鑰。受攻擊者花費了相對多的計算資源來求解無用的冪係數而不是在做真正的工作。
3、沒辦法防止重演攻擊。
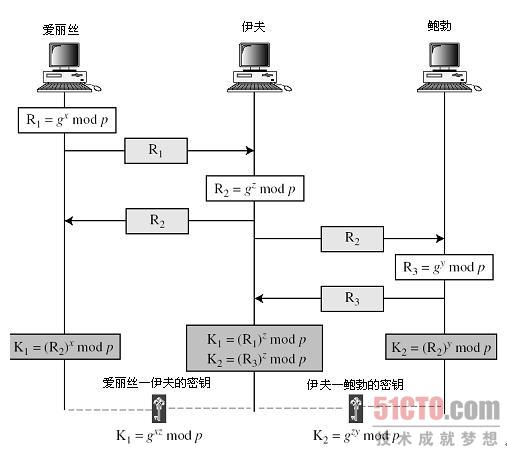
4、容易遭受中間人的攻擊。第三方C在和A通訊時扮演B;和B通訊時扮演A。A和B都與C協商了一個金鑰,然後C就可以監聽和傳遞通訊量。中間人的攻擊按如下進行:
(1)B在給A的報文中傳送他的公開金鑰。
(2)C截獲並解析該報文。C將B的公開金鑰儲存下來並給A傳送報文,該報文具有B的使用者ID但使用C的公開金鑰YC,仍按照好像是來自B的樣子被髮送出去。A收到C的報文後,將YC和B的使用者ID儲存在一塊。類似地,C使用YC向B傳送好像來自A的報文。
(3)B基於私有金鑰XB和YC計算祕密金鑰K1。A基於私有金鑰XA和YC計算祕密金鑰K2。C使用私有金鑰XC和YB計算K1,並使用XC和YA計算K2。
(4)從現在開始,C就可以轉發A發給B的報文或轉發B發給A的報文,在途中根據需要修改它們的密文。使得A和B都不知道他們在和C共享通訊。
Oakley演算法是對Diffie-Hellman金鑰交換演算法的優化,它保留了後者的優點,同時克服了其弱點。
Oakley演算法具有五個重要特徵:
1、它採用稱為cookie程式的機制來對抗阻塞攻擊。
2、它使得雙方能夠協商一個全域性引數集合。
3、它使用了現時來保證抵抗重演攻擊。
4、它能夠交換Diffie-Hellman公開金鑰。
5、它對Diffie-Hellman交換進行鑑別以對抗中間人的攻擊。
Oakley可以使用三個不同的鑑別方法:
1、數字簽名:通過簽署一個相互可以獲得的雜湊程式碼來對交換進行鑑別;每一方都使用自己的私鑰對雜湊程式碼加密。雜湊程式碼是在一些重要引數上生成的,如使用者ID和現時。
2、公開金鑰加密:通過使用傳送者的私鑰對諸如ID和現時等引數進行加密來鑑別交換。
3、對稱金鑰加密:通過使用某種共享金鑰對交換引數進行對稱加密,實現交換的鑑別。
這種演算法的關鍵是在這個式中
b=ai mod p, 0<=i<=p-1
如果知道a, i, p可以很方便的算出b的值,但是知道b, a, p的情況下想要算出i的值卻非常難。所以如果只要突破這個點,就需要能在足夠短的時間內算出i的值是多少。我相信不久的將來,隨著量子計算機的發展,破解這種加密方式將不再是問題,任何一種依靠計算複雜度來保證資料安全性的加密方式都將會被淘汰,應運而生的將是更加先進可靠的加密方式。