網上看了這篇文章後還是感覺有些地方講的沒有詳細的證明所以添加了一點 紅色字是博主寫的

求字串的迴圈最小表示：

上面說的兩個字元串同構的，並沒有直接先求出Min(s)，而是通過指標移動，當某次匹配串長時，那個位置就是Min(s)。而這裡的問題就是：不是給定兩個串，而是給出一個串，求它的Min(s)，eg：Min(“babba”) = 4。那麼由於這裡並非要求兩個串的同構，而是直接求它的最小表示，由於源串和目標串相同，所以處理起來既容易又需要有一些變化：我們仍然設定兩個指標，i, j，其中i指向0，j指向1，仍然採用上面的滑動方式：

(1)  利用兩個指標i， j。初始化時i指向0, j指向1。

(2)  k = 0開始，檢驗s[i+k] 與 s[j+k] 對應的字元是否相等，如果相等則k++，一直下去，直到找到第一個不同，(若k試了一個字串的長度也沒找到不同，則那個位置就是最小表示位置，演算法終止並返回)。則該過程中，s[i+k] 與 s[j+k]的大小關係，有三種情況：

  證明的時候假設（i<j）的，無傷大雅 ；

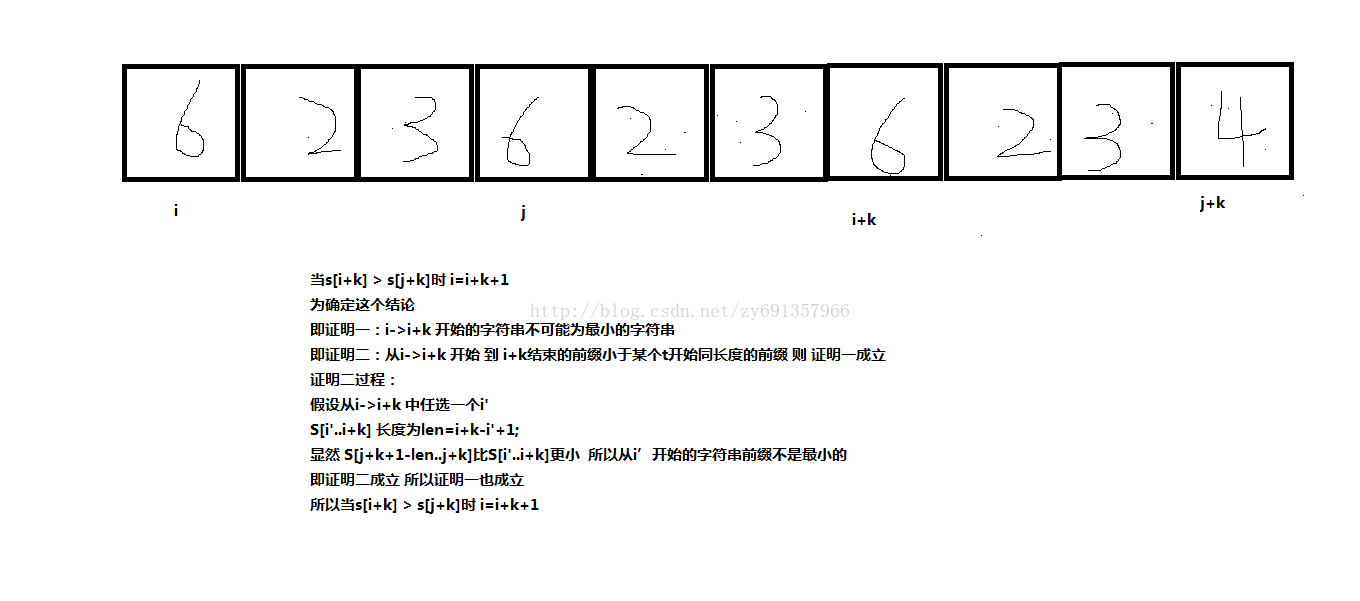
     (A). s[i+k] > s[j+k]，則i滑動到i+k+1處 --- 即s1[i->i+k]不會是該迴圈字串的“最小表示”的字首。

證明如下

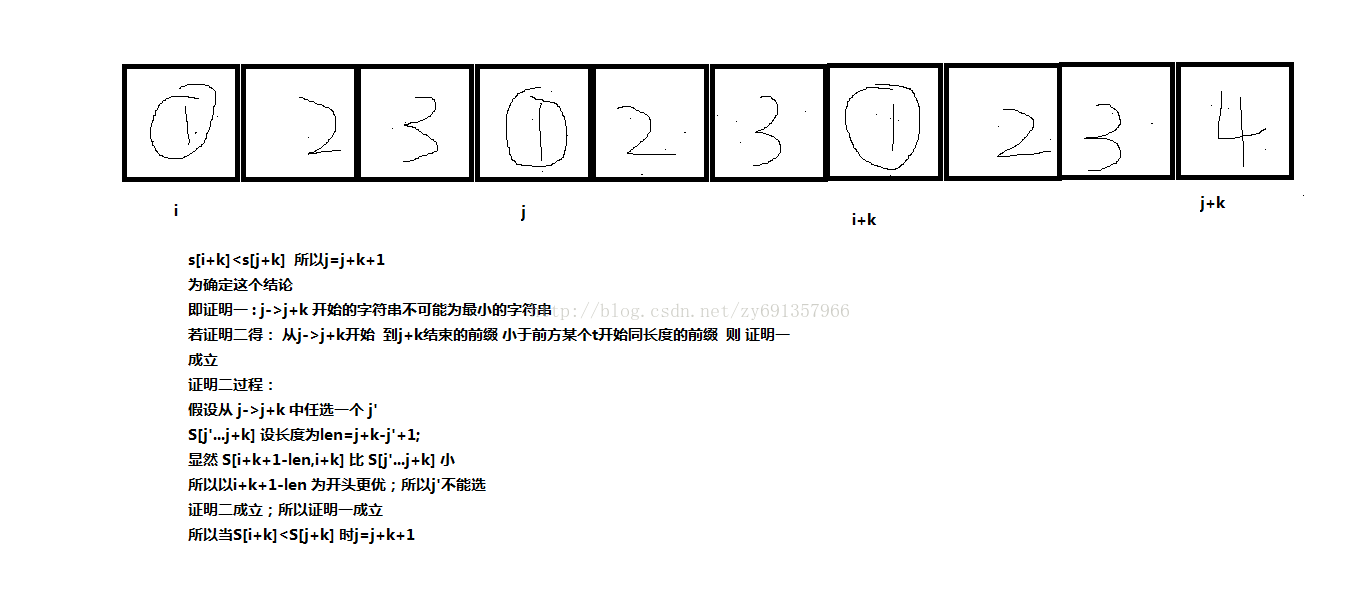
     (B). s[i+k] < s[j+k]，則j滑動到j+k+1處，原因同上。

證明如下

     (C). s[i+k] = s[j+k]，則 k++； if (k == len) 返回結果。 

    注:這裡滑動方式有個小細節，若滑動後i == j，將正在變化的那個指標再+1。直到p1、p2把整個字串都檢驗完畢，返回兩者中小於 len 的值。

(3)   如果 k == len， 則返回i與j中的最小值

      如果 i >= len   則返回j

      如果 j >= len   則返回i

如果看了上一篇文章 很容易對這裡的i,j 產生誤會  誤以為i為ans,j為比較指標

實際上這題中 i,j 都可能存有ans 兩者互相更新，直到有一個更新後超過了len（包括len） 的時候 另一個即為正解

(4)   進一步的優化，例如：i要移到i+k+1時，如果i+k+1 <= p2的話，可以直接把i移到 j+1，因為，j到j+k已經檢驗過了該字首比以i到i+k之間任何一個位字首都小；j時的類似，移動到i+1。

這個優化就無需解釋了

至此，求一個字串的迴圈最小表示在O(n)時間實現，感謝大牛的論文。其中實現時的小細節“如果滑動後p1 == p2，將正在變化的那個指標再+1”，開始沒有考慮，害得我想了幾個小時都覺得無法進行正確的移動。具體例題有兩個：http://acm.zju.edu.cn 的2006和1729題。一個是10000規模一個是100000規模。執行時間前者是0S，後者是0.05S。

int MinimumRepresentation(int *s, int l)  
{  
	int i,j,k;
	i=0;j=1;k=0;
	while(i<l&&j<l)
	{
		k=0;
		while(s[i+k]==s[j+k]&&k<l) k++;
		if(k==l) return i;
		if(s[i+k]>s[j+k]) 
		 if(i+k+1>j) i=i+k+1;
		 else i=j+1;
		else if(j+k+1>i) j=j+k+1;
		else  j=i+1; 
	}
	if(i<l) return i;
	else return j;
}