EM演算法及GMM(高斯混合模型)的詳解
一、預備知識
1.1、協方差矩陣
在高維計算協方差的時候,分母是n-1,而不是n。協方差矩陣的大小與維度相同。
1.2、黑塞矩陣
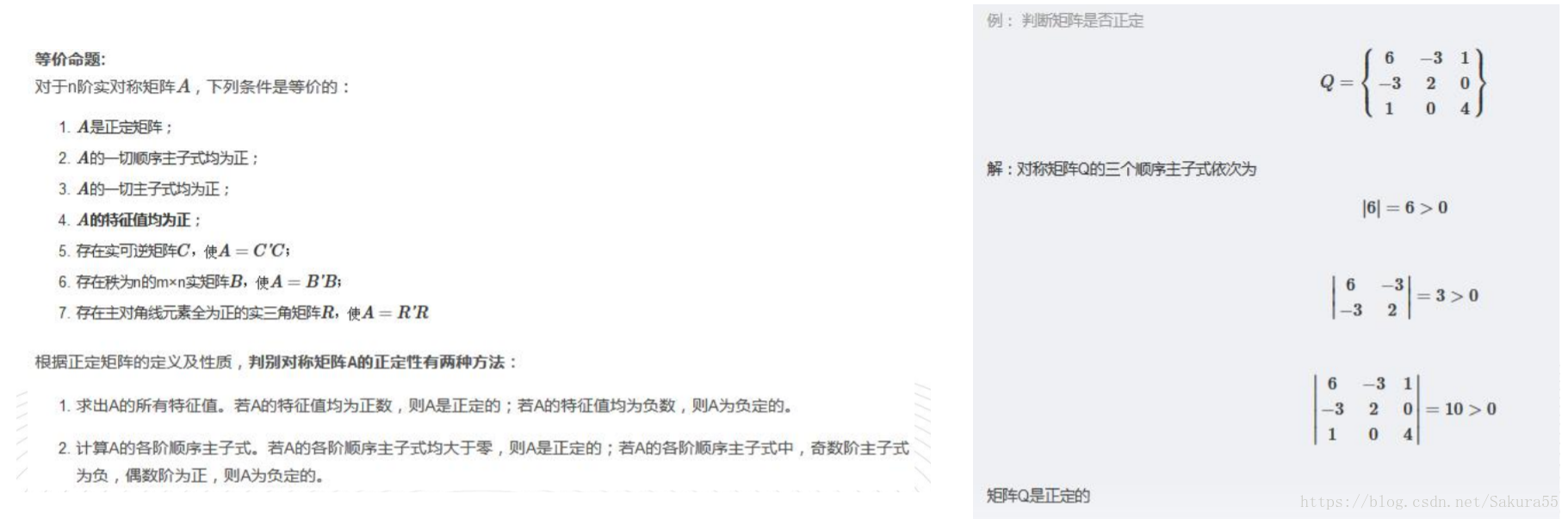
1.3、正定矩陣


二、高斯混合模型
點模式的分析中,一般會考察如下五種內容:
● 點的疏密,包括點資料的分佈探索,是否一致、均勻或者不均勻。
● 點的方位,包括點的分佈和方向。
● 點的數量:多少(極值和均值)。
● 點的大小:代表的含義(如點一個點代表多少人口)。
● 其他,如點的一些動態變化等。
2.1、標準差橢圓
這演算法最早是由美國南加州大學(UniversityofSouthern California)社會學教授韋爾蒂.利菲弗(D. Welty Lefever)在1926年提出,所以有的書裡面,也把這個演算法稱為Lefever‘s “Standard
DeviationalEllipse”(利菲弗方向性分佈
其實演算法很簡單,要畫出一個橢圓:
1、確定圓心。
2、確定旋轉角度。
3、確定XY軸的長度。

基本概念:
1、橢圓的長半軸表示的是資料分佈的方向,短半軸表示的是資料分佈的範圍,長短半軸的值差距越大(扁率越大),表示資料的方向性越明顯。反之,如果長短半軸越接近,表示方向性越不明顯。如果長短半軸完全相等,就等於是一個圓了,圓的話就表示沒有任何的方向特徵。
2、短半軸表示資料分佈的範圍,短半軸越短,表示資料呈現的向心力越明顯;反之,短軸越長,表示資料的離散程度越大。同樣,如果短半軸與長半軸完全相等了,就表示資料沒有任何的分佈特徵。
3、中心點表示了整個資料的中心位置
4、有的同學會很疑惑,為什麼你畫的這個橢圓,還有很多的點都在外面,沒有把所有的點都包含進去?那麼就是就是“標準差橢圓”這個名詞裡面的“標準差”的含義所在了。
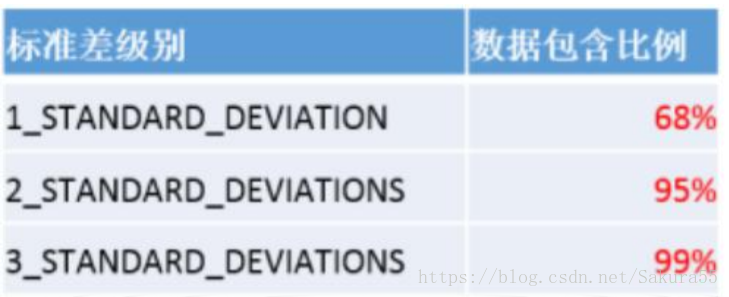
當要素具有空間正態分佈時(即這些要素在中心處最為密集,而在接近外圍時會逐漸變得稀疏),第一級標準差(預設值)範圍可將約佔總數 68%的輸入要素的質心包含在內。第二級標準差範圍會將約佔總數 95%的要素包含在內,而第三級標準差範圍則會覆蓋約佔總數 99%的要素的質心。
所以,當你選擇不同標準差等級的時候,你發現你的中心點的位置也可能不同。當然,作為空間分析工具,方向分佈一樣可以進行加權計算,這個計算主要還是與中心點的位置確定以及橢圓標準差等級生成的橢圓大小有關係。
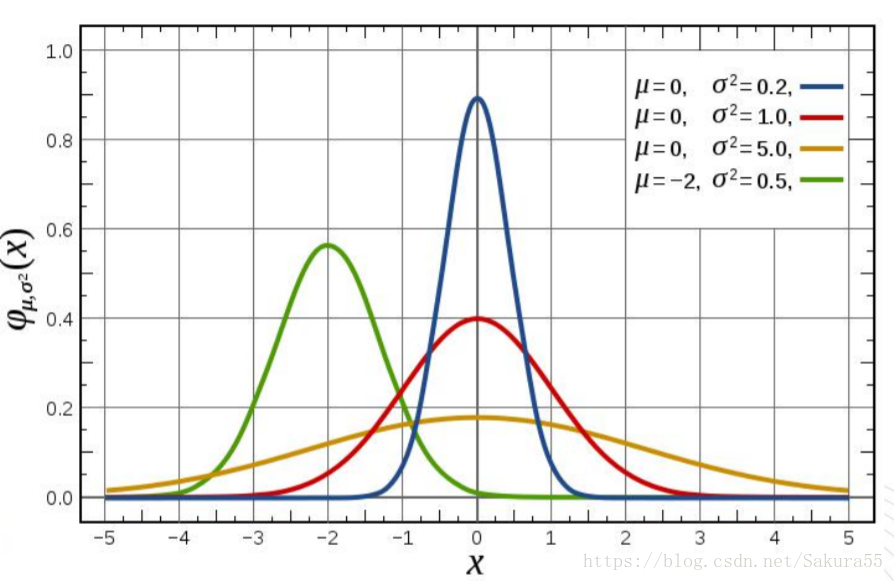
2.2、高斯混合模型(GMM)
高斯混合模型(Gaussian Mixed Model)指的是多個斯分佈函式的線性組合,理論上GMM可以擬合出任意型別的分佈,通常用於解決同一集合下的資料包含多個不同的分佈的情況(或者是同一類分佈但引數不一樣,或者是不同型別的分佈,比如正態分佈和伯努利分佈)。
如圖1,圖中的點在我們看來明顯分成兩個聚類。這兩個聚類中的點分別通過兩個不同的正態分佈隨機生成而來。但是如果沒有GMM,那麼只能用一個的二維高斯分佈來描述圖1中的資料。圖1中的橢圓即為二倍標準差的正態分佈橢圓。這顯然不太合理,畢竟肉眼一看就覺得應該把它們分成兩類。
這時候就可以使用GMM了!如圖2,資料在平面上的空間分佈和圖1一樣,這時使用兩個二維高斯分佈來描述圖2中的資料,分別記為N(μ1,Σ1)和N(μ2,Σ2). 圖中的兩個橢圓分別是這兩個高斯分佈的二倍標準差橢圓。可以看到使用兩個二維高斯分佈來描述圖中的資料顯然更合理。實際上圖中的兩個聚類的中的點是通過兩個不同的正態分佈隨機生成而來。如果將兩個二維高斯分佈N(μ1,Σ1)和N(μ2,Σ2)合成一個二維的分佈,那麼就可以用合成後的分佈來描述圖2中的所有點。最直觀的方法就是對這兩個二維高斯分佈做線性組合,用線性組合後的分佈來描述整個集合中的資料。這就是高斯混合模型(GMM)。
從上面的分析中我們可以看到 GMM 和 K-means 的迭代求解法其實非常相似(都可以追溯到 EM 演算法),因此也有和 K-means 同樣的問題──並不能保證總是能取到全域性最優,如果運氣比較差,取到不好的初始值,就有可能得到很差的結果。對於 K-means 的情況,我們通常是重複一定次數然後取最好的結果,不過 GMM每一次迭代的計算量比 K-means 要大許多,一個更流行的做法是先用 K-means(已經重複並取最優值了)得到一個粗略的結果,然後將其作為初值(只要將 K- means 所得的 centroids 傳入 gmm 函式即可),再用 GMM 進行細緻迭代
2.3、多元高斯混合
2.4、應用場景
設樣本集X=x1,x2,…,xN,其中N=100 ,p(xi|θ)為概率密度函式,表示抽到男生xi(的身高)的概率。由於100個樣本之間獨立同分布,所以我同時抽到這100個男生的概率就是他們各自概率的乘積,也就是樣本集X中各個樣本的聯合概率,用下式表示:
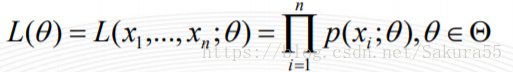
這個概率反映了,在概率密度函式的引數是θ時,得到X這組樣本的概率。 我們需要找到一個引數θ,使得抽到X這組樣本的概率最大,也就是說需要其對應的似然函式L(θ)最大。滿足條件的θ叫做θ的最大似然估計量,記為
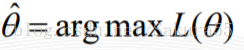
2.5、kmeans應用

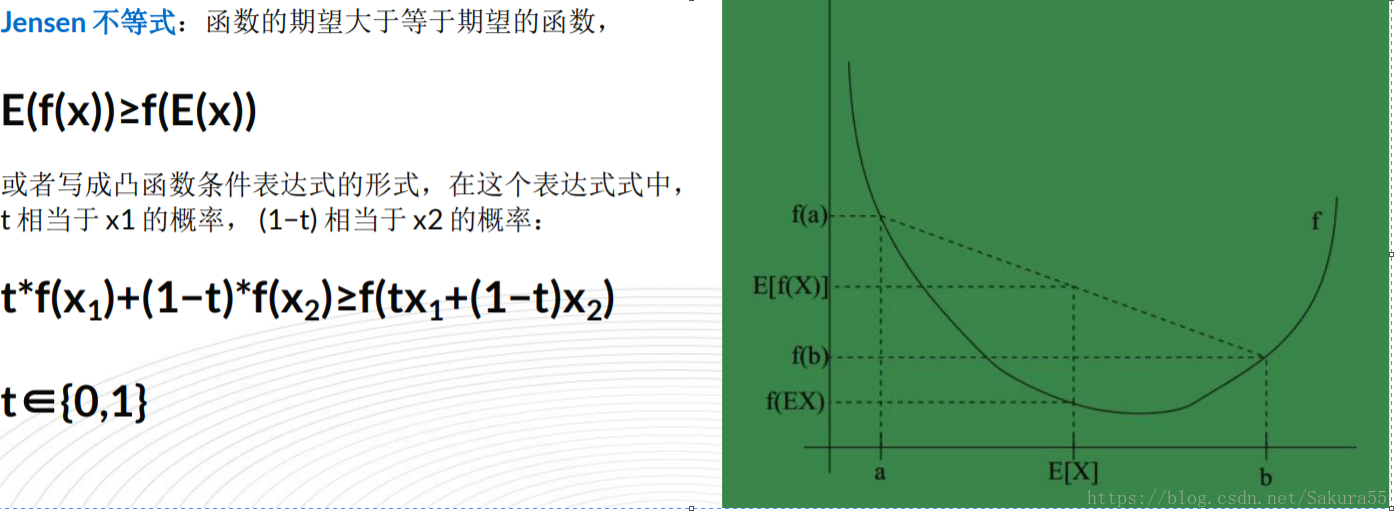
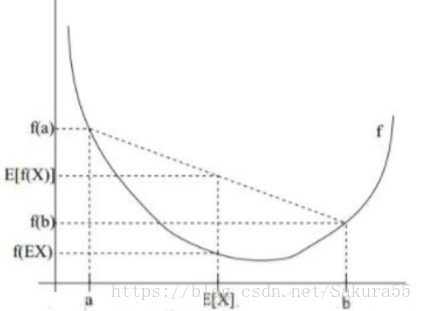
2.6、基本Jensen不等式應用

設f是定義域為實數的函式,如果對於所有的實數x,f(x)的二次導數大於等於0,那麼f是凸函式。Jensen不等式表述如下:如果f是凸函式,X是隨機變數,那麼E[f(X)]≥f(E[X])。當且僅當X是常量時,上式取等號。其中,E[x]表示x的數學期望。
1、Jensen不等式應用於凹函式時,不等號方向反向。當且僅當X是常量時,Jensen不等式等號成立。
2、關於凸函式,百度百科中是這樣解釋的——“對於實數集上的凸函式,一般的判別方法是求它的二階導數,如果其二階導數在區間上非負,就稱為凸函式(向下凸)”。
例如,實線f是凸函式,X是隨機變數,有0.5的概率是a,有0.5的概率是b。X的期望值就是a和b的中值了,圖中可以看到E[f(X)]≥f(E[X])成立。
三、計算流程
(1)初始化引數:先初始化男生身高的正態分佈的引數:如均值=1.7,方差=0.1
(2)計算每一個人更可能屬於男生分佈或者女生分佈;
(3)通過分為男生的n個人來重新估計男生身高分佈的引數(最大似然估計),女生分佈也按照相同的方式估計出來,更新分佈。
(4)這時候兩個分佈的概率也變了,然後重複步驟(1)至(3),直到引數不發生變化為止。
已知的有兩個:
樣本服從的分佈模型、隨機抽取的樣本;
未知的有一個:
模型的引數;
根據已知條件,通過極大似然估計,求出未知引數。極大似然估計就是用來估計模型引數的統計學方法。
EM流程
有時候因為樣本的產生和隱含變數有關(隱含變數是不能觀察的),而求模型的引數時一般採用最大似然估計,由於含有了隱含變數,所以對似然函式引數求導是求不出來的,這時可以採用EM演算法來求模型的引數的(對應模型引數個數可能有多個),EM演算法一般分為2步:
E步:選取一組引數,求出在該引數下隱含變數的條件概率值;
M步:結合E步求出的隱含變數條件概率,求出似然函式下界函式(本質上是某個期望函式)的最大值。
重複上面2步直至收斂: