圖之關節點和重連通分量
一、介紹
關節點問題主要是用線上路架設上,一旦關節點損壞,線路網就斷開了。因此為避免這種情況,需要將網做出重連通圖。關節點更像是把圖分成了兩部分,而這兩部分只通過這個關節點連結。顯然如果這個關節點斷了,這兩個子圖就無法再通訊了。
二、演算法
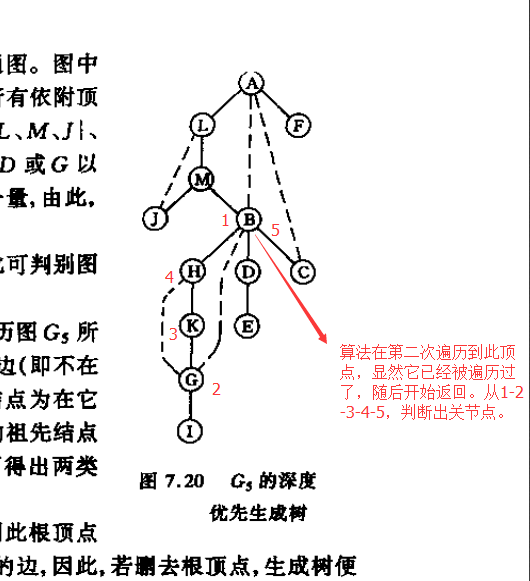
基於深度搜索,有以下特性:

上面的low[w]有點不好理解,其實大致意思,如果我們在進行深度搜索時,到最深處是一個已被訪問的頂點。這是我們判斷這個已被訪問的頂點是第幾次被訪問的。如果它被訪問的時間早於當前父頂點,那說明這個頂點在樹上處於比父頂點更高的地方。那麼顯然,父頂點和已被訪問的頂點存在一個迴路。

三、鄰接表儲存
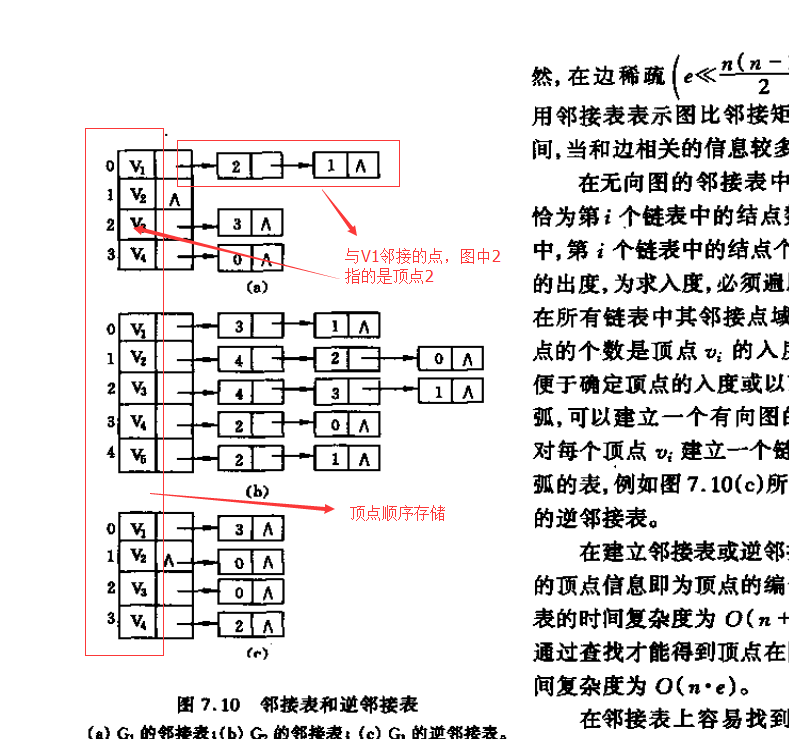
上述演算法使用的鄰接表儲存的圖,補充一下儲存結構:
相關推薦
圖之關節點和重連通分量
一、介紹 關節點問題主要是用線上路架設上,一旦關節點損壞,線路網就斷開了。因此為避免這種情況,需要將網做出重連通圖。關節點更像是把圖分成了兩部分,而這兩部分只通過這個關節點連結。顯然如果這個關節點斷了,這兩個子圖就無法再通訊了。 二、演算法 基於深
資料結構之圖的關節點和重連通分量
本著業界良心,我感覺這個連結中關於圖的關節點講得很不錯。什麼是關節點?在某圖中,若刪除頂點V以及V相關的邊後,圖的一個連通分量分割為兩個或兩個以上的連通分量,則稱頂點V為該圖的一 個關節點。
圖->連通性->關節點和重連通分量
文字描述 相關定義:假若在刪去頂點v以及和v相關聯的各邊之後,將圖的一個連通分量分割成兩個或兩個以上的連通分量,則稱頂點v為該圖的一個關節點.一個沒有關節點的連通圖稱為重連通圖. 在重連通圖上,任意一對頂點之間至少存在兩條路徑, 則在刪去某個頂點以及依附於該頂點的各邊時也不破壞圖的連通性.若在連通圖上至
溫習Algs4 (四):有向圖, 拓撲排序和強連通分量
有向圖, 拓撲排序和強連通分量 有向圖 Digraph.java 有向環 DiCycle.java 深度優先搜尋序列 DFSOrder.java 拓撲排序 Topo
關節點及重連通圖
這個內容為什麼想放在這個時候就放出來呢?因為剛剛才把TOP排序講完,所以我們跳過關鍵路徑『有什麼關聯嗎?』,直接進入關節點和重連通圖。 一、關節點:又稱割點,是維繫一個圖能夠連通的節點(就是說沒有這個節點,這個圖就不連通),若從連通圖中刪除點V,就會使這個圖割
CentOs之關機和重啟命令
centos poweroff inittab 修改 HA 命令 指定 log 建議 shutdown命令 shutdown [選項] 時間 -c:取消前一個關機命令 -h:關機 -r:重啟 [root@localhost ~]# date 2017年 06月 21日
前端性能優化之重排和重繪
doc 重復 立即執行 selector add 顯示與隱藏 one 改變樣式 ref 前言,最近利用碎片時間拜讀了一下尼古拉斯的另一巨作《高性能JavaScript》,今天寫的文章從“老生常談”的頁面重繪和重排入手,去探究這兩個概念在頁面性能提升上的作用。 一.重排 &a
學前班第1課第1節_怎麼看原理圖之GPIO和閘電路
原理圖主要分為三類 一、管腳類即GPIO和閘電路 1.1輸入、輸出引腳、上拉電阻、三極體 1.2與門、或門、非門 1.3中斷 二、協議類 2.1 UART 2.2 I2C 2.3 SPI 2.4 NAND 2.5 LCD 三、類似記憶體的介面
前端效能優化之重排和重繪
前言,最近利用碎片時間拜讀了一下尼古拉斯的另一鉅作《高效能JavaScript》,今天寫的文章從“老生常談”的頁面重繪和重排入手,去探究這兩個概念在頁面效能提升上的作用。 一.重排 & 重繪 有經驗的大佬對這個概念一定不會陌生,“瀏覽器輸入URL發生了什麼”。估計大家已經爛熟於
【軟考路上】——用例圖之include和extend
記得去年剛學UML的時候,寫了一篇用例圖的部落格——《UML圖—用例圖》。 2011年5月的軟考下午題,考到了用例圖,突然感覺對用例圖中的include和extend概念
Servlet之轉發和重定向的區別
邏輯 jsp 一個 地址 span 目標 主頁 servlet status 應該是出自github上的項目JavaGuide 轉發是服務器行為,重定向是客戶端行為。轉發(Forword) 通過RequestDispatcher對象的forward(HttpServl
樂字節-Java8新特性之Base64和重復註解與類型註解
ref sin pre easy 處理 on() append 靈活 rfc 上一篇小樂給大家說了《樂字節-Java8新特性之Date API》,接下來小樂繼續給大家說一說Java8新特性之Base64和重復註解與類型註解。 一、Base64 在Java 8中,內
c2java 第7篇 圖的連通分量,關節點和橋
圖的連通分量,關節點和橋 ==== 對於有向圖,我們稱其一個子圖是強連通分量,是指任意兩點u,v, 都有兩條路徑u到v和v到u。對於連通無向圖,我門稱其一個子圖是雙連通分量,是指任意兩點u,v,存在一個圈包含u,v。與無向圖相關聯的還有關節點x,是指去掉x,圖不連通;橋(u
無向圖的割頂和橋,無向圖的雙連通分量入門詳解及模板 -----「轉載」
dbr break nts word 否則 mark push gravity 無向連通圖 https://blog.csdn.net/stillxjy/article/details/70176689 割頂和橋:對於無向圖G,如果刪除某個節點u後,連通分量數目
圖之強連通、強連通圖、強連通分量 Tarjan算法
The 當前 one 自身 com name cxf 單個 con 原文地址:https://blog.csdn.net/qq_16234613/article/details/77431043 一、解釋 在有向圖G中,如果兩個頂點間至少存在一條互相可達路徑,稱兩個頂點強連
DFS的運用(二分圖判定、無向圖的割頂和橋,雙連通分量,有向圖的強連通分量)
part str stack void div prev this 沒有 2-sat 一、dfs框架: 1 vector<int>G[maxn]; //存圖 2 int vis[maxn]; //節點訪問標記 3 void dfs(int u
圖->連通性->無向圖的連通分量和生成樹
文字描述 對無向圖進行遍歷時,對於連通圖,僅需從圖中任一頂點出發,進行深度優先搜尋或廣度優先搜尋,便可訪問到圖中所有頂點。但對非連通圖,則需從多個頂點出發搜尋,每一次從一個新的起始點出發進行搜尋過程得到的頂點訪問序列恰為其各個連通分量中的頂點集。 對於非連通圖,每個連通分量中的頂點集,和遍歷時走過
圖之鄰接矩陣,深度遍歷,廣度遍歷,連通分量個數
1.深度遍歷 DFS 類似於樹的先根遍歷 如圖,上述圖的深度遍歷輸出為ADCBE 給出一個圖的鄰接矩陣,對圖進行深度優先搜尋,從頂點0開始 class Graph { private: int flag[N];//狀態陣列 int
POJ 2186 Popular Cows(圖論之強連通分量)
強連通分量之於有向圖,與並查集之於無向圖,在概念上極其相似,都是尋找互相聯絡的小部分內容。 POJ 2186 Popular Cows Description Every cow's dream is to become the most popular cow in the herd.
溫習Algs4 (三):無向圖, 搜尋和連通分量
無向圖, 搜尋和連通分量 無向圖 Graph.java 搜尋 Visitor.java Search.java 深度優先搜尋 DepthFirstSearch.java 廣