想象一下我們有如下兩個任務:

• 我現在想騎一輛小黃車，我想查詢離我最近的k輛小黃車.
• 找到百度地圖中顯示在螢幕上區域中的所有酒店

這兩個任務均可以用kd-tree來解決
kd-tree 主要兩個用途:

• 查詢離某個點的最近的k 個鄰居,
• 搜尋某個區域內的所有點.

後者在計算幾何中稱為範圍查詢,例如查詢某個平面區域內的點的個數.

kd-tree是什麼玩意兒

kd-tree就是高維平衡樹……
kd-tree 是將平面點集進行一個分割，對某一個維度滿足左子樹和右子樹的偏序關係

若你只對程式碼感興趣請直接移動到文末
程式碼文末

建樹

以二維平面為例
在根節點以某一維度對點集進行分割，比如以x

擴充套件到多維的情形則是:

每一層輪流選擇某一維度作為切割方向，找到沿著這一方向上的中位數節點，將其作為根，遞迴建樹則行

例項

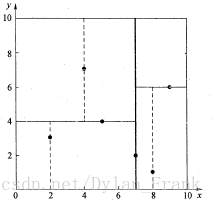
假設有6個二維資料點{（2,3），（5,4），（9,6），（4,7），（8,1），（7,2）}，資料點位於二維空間內（如圖1中黑點所示）。k-d樹演算法就是要確定圖1中這些分割空間的分割線（多維空間即為分割平面，一般為超平面）。下面就要通過一步步展示k-d樹是如何確定這些分割線的。

k-NN 查詢

虛擬碼

k_close(p,o,k,)//查詢點p,樹當前節點o,近鄰數目k
1. 從根節點開始遞迴的查詢，根據p在節點的左邊還是右邊，決定遞迴方向
2. 若到達葉節點,則將其作為當前最優節點
3. 回溯:
(1) 若當前節點比當前最優點更優，則將其作為當前最優節點
(2) 判斷左子樹是否存在最優點，若有則遞迴下去
4. 當根節點搜尋完畢，則查詢結束

實現細節

具體實現的時候需要說明的是，可以用一個優先佇列儲存最優的k個節點，這樣每次比對回溯節點是否比當前最優點更優的時候，就只需用當前最優點中裡p最遠的節點來比對，而這個工作對於優先佇列來說是O

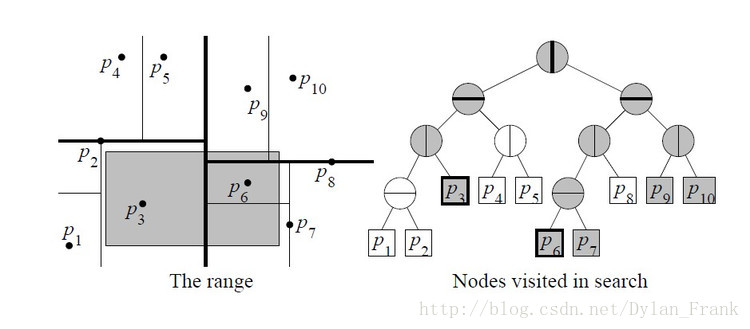
範圍查詢

給定一個平面矩形範圍，問其中有多少個點.如圖

虛擬碼

find(region,o)//範圍，當前節點
ret =0
if 葉子節點：　ret += (o在region 內部) ,return
判斷當前節點是否在範圍內,在就+1
if 左子樹在其內部　報告左子樹內所有節點，
else 判斷是否與左子樹相交，若是則遞迴進入左子樹，查詢ret += (region,lc)
右子樹同理

複雜度

範圍查詢複雜度

由於kd-tree每一層都是對平面的劃分，我們考慮其孫子輩節點.查詢只會對那些與其相交的節點遞迴查詢，因此只需要判斷相交區域數目就行了,
如下圖

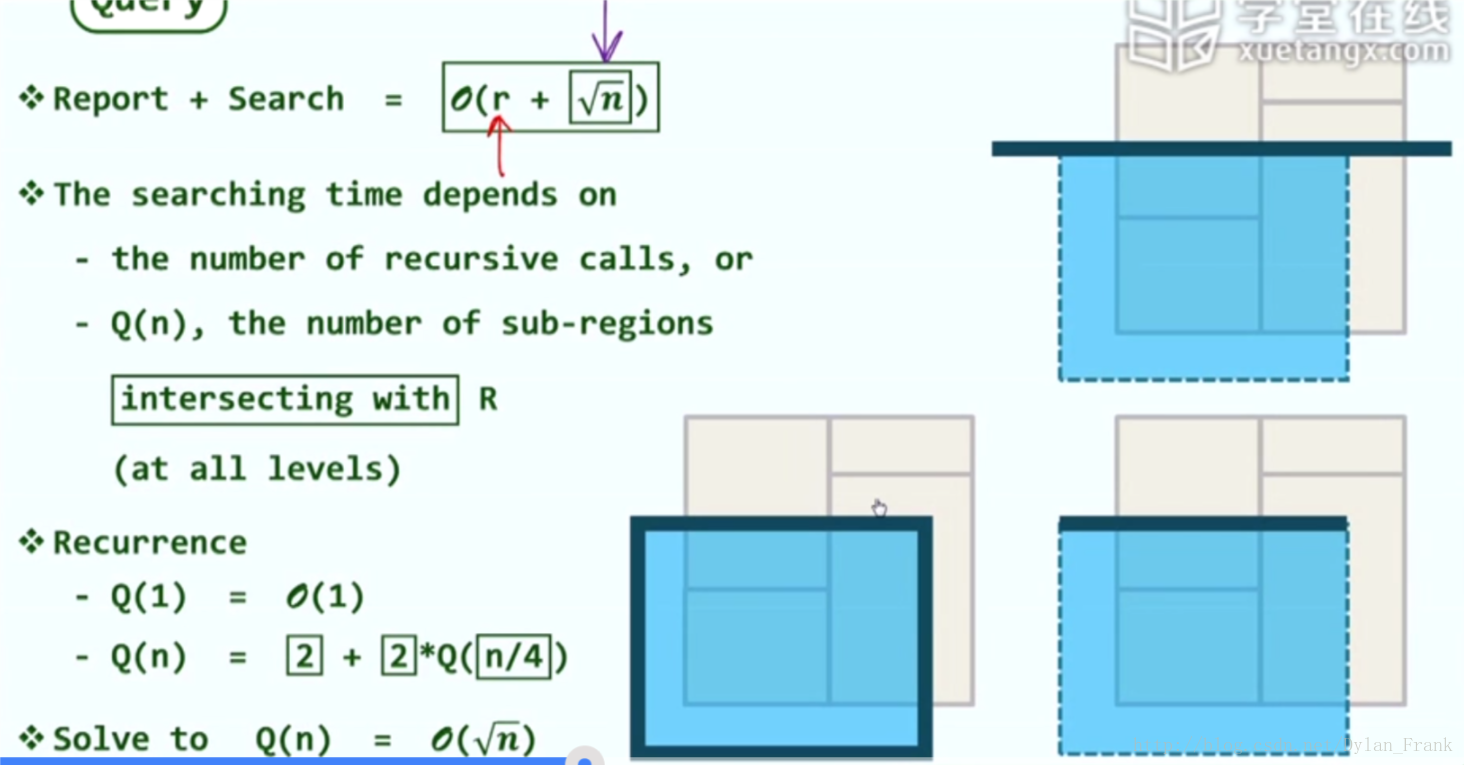
將其中一條邊延展出去後至多會與兩個區域相交，因此:

範圍查詢的優化

我們會發現有很多遞迴都是不需要的因為，有些時候某個子節點的區域已經完全包含其中了

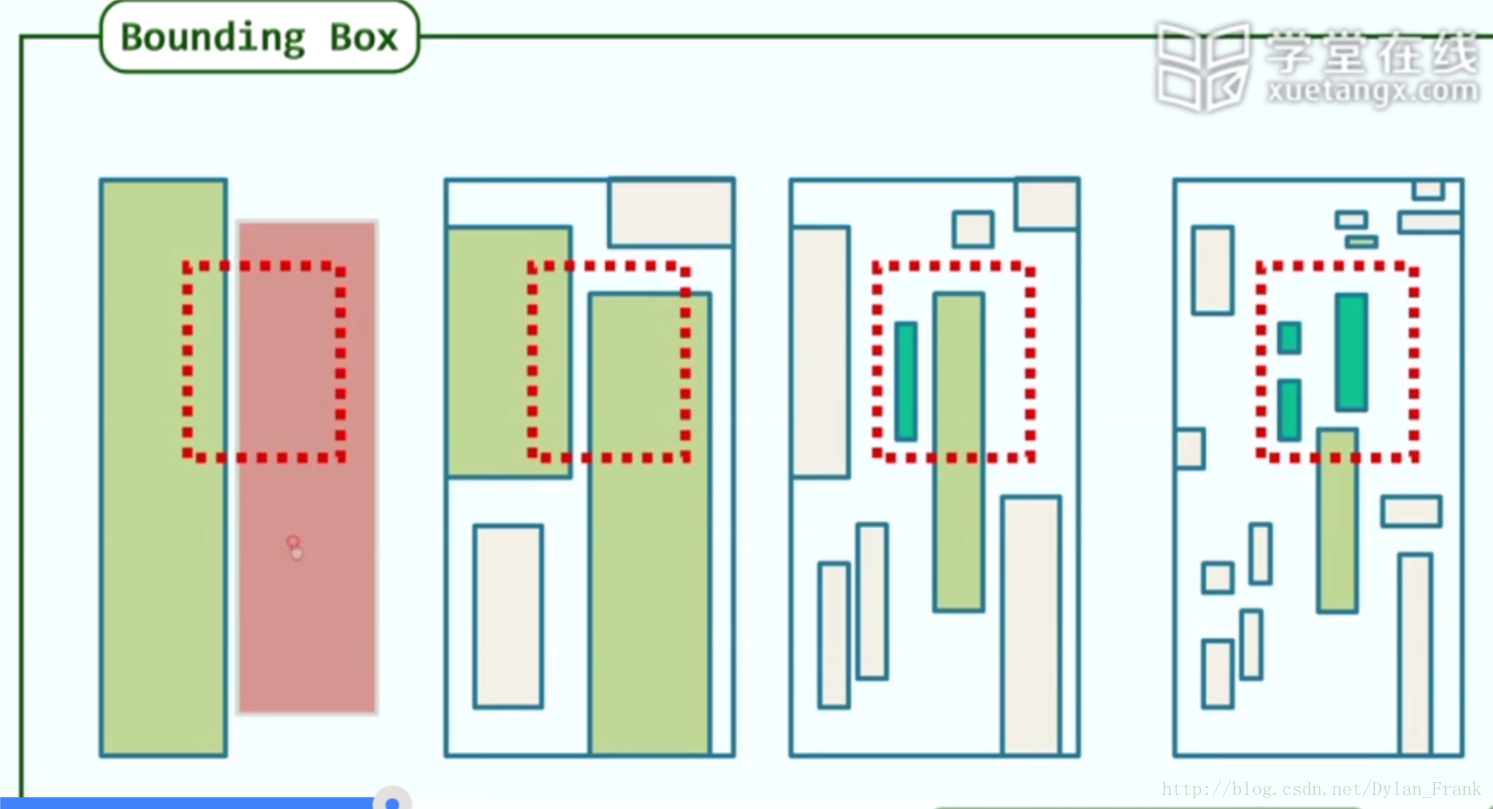
所以我們可以在節點中記錄他相應管轄的區域，這樣就能提前終止遞迴了.
詳細程式碼見文末

超出2d

不難發現在更高緯度的時候也是一樣的，我們按照每個緯度切分一次就行了,
不過複雜度會有所提高，
一般的在d維空間中進行範圍查詢的複雜度是O(nd−1d) 非常高，所以不太推薦用kd-tree做範圍查詢，範圍查詢我們有更高效的資料結構—–range tree 2d的時候查詢時間複雜度為O(logn)

程式碼

本程式碼 k_close 查詢經過HDU 4347 測試
那個題是在5維空間中查詢k-NN,給的時限是8s

AC程式碼

範圍查詢部分，只經過個人資料測試，未在oj 測試,若有題目請聯絡
限於本人c++有限，設計的不夠好.

int _idx;//比較維度
struct KDNode{
    const static int max_dims = 5;
    int featrue[max_dims];
    int size;//子樹節點個數
    int region[max_dims][2];//每個維度最大值最小值
    int dim;
    bool operator < (const KDNode& o)const{
        return featrue[_idx]<o.featrue[_idx];
    }
};
struct KDTree{
    int dims;
    KDNode Node[maxn];
    KDNode data[maxn<<2];
    bool flag[maxn<<2];
    priority_queue<pair<int,KDNode> > Q;//查詢結果佇列
    void build(int l,int r,int o,int dep,bool clc_region = false){
        //最後一個引數表明是否記錄區域大小
        if(l>r)return;
        _idx = dep % dims;
        int lc = o<<1,rc = o<<1|1;
        flag[o] = true;
        flag[lc]=flag[rc] = 0;
        int mid = (l+r) >> 1;
        nth_element(Node+l,Node+mid,Node+r+1);
        data[o] = Node[mid];data[o].dim = _idx;
        // std::cout <<"node "<< o << '\n';
        // std::cout << _idx << '\n';
        // for(int i=0 ; i<dims ; ++i)std::cout << data[o].featrue[i] << ' ';std::cout  << '\n';
        data[o].size = r-l+1;
        if(clc_region){
            for(int i=0 ; i<dims ; ++i){
                _idx = i;
                data[o].region[i][0] = min_element(Node+l,Node+r+1)->featrue[i];
                data[o].region[i][1] = max_element(Node+l,Node+r+1)->featrue[i];
            }
            _idx = dep%dims;
        }
        build(l,mid-1,lc,dep+1,clc_region);
        build(mid+1,r,rc,dep+1,clc_region);
    }

    void k_close(const KDNode& p,int k,int o){
        if(!flag[o])return;
        int dim = data[o].dim;
        int lc = o<<1;int rc = o<<1|1;
        if(p.featrue[dim] >data[o].featrue[dim])swap(lc,rc);
        if(flag[lc])k_close(p,k,lc);
        pair<int,KDNode> cur(0,data[o]);
        for(int i=0 ; i<dims ; ++i)cur.fi+=SQ(p.featrue[i]-data[o].featrue[i]);
        bool fg = false;//右子樹遍歷標誌
        if(Q.size() < k){
            Q.push(cur);fg =1;
        }else{
            if(cur.fi < Q.top().fi){
                Q.pop();Q.push(cur);
            }
            fg = SQ(p.featrue[dim]-data[o].featrue[dim]) < Q.top().fi;
        }
        if(flag[rc] && fg)k_close(p,k,rc);
    }
    int  check(int region[][2],int o){
        //1表示相交
        //－１表示全屬於
        //0表示不相交
        if(!flag[o])return 0;
        bool fg = true;
        for(int i=0 ; i<dims ; ++i){
            if(data[o].region[i][0] < region[i][0] || data[o].region[i][1] > region[i][1]){
                fg = false;break;
            }
        }
        int d = data[o].dim;
        return fg?-1 : data[o].region[d][1] > region[d][0] || data[o].region[d][0]<region[d][1];
    }
    int find_size(int region[][2],int o){
        //查詢範圍內的點數
        //預設建樹時有ｒｅｇｉｏｎ記錄
        if(!flag[o])return 0;
        int ret =0;
        bool fg =1 ;//當前點是否在範圍內
        for(int i=0 ; i<dims ; ++i)
            if(data[o].featrue[i]<region[i][0]||data[o].featrue[i]>region[i][1]){
                fg = 0;break;
            }
        ret += fg;
        int lc = o<<1,rc = o<<1|1;
        int lstate = check(region,lc),rstate = check(region,rc);
        if(lstate ==-1)ret += data[lc].size;
        else if(lstate == 1)ret += find_size(region,lc);
        if(rstate ==-1)ret += data[rc].size;
        else if(rstate == 1)ret += find_size(region,rc);
        return ret;
    }
};

侷限

以上只是一顆靜態樹不支援加點和刪除.