二叉樹的相關操作(上)
本文章主要介紹二叉樹的概念、特點、以及二叉樹的相關操作。
1.二叉樹的概念
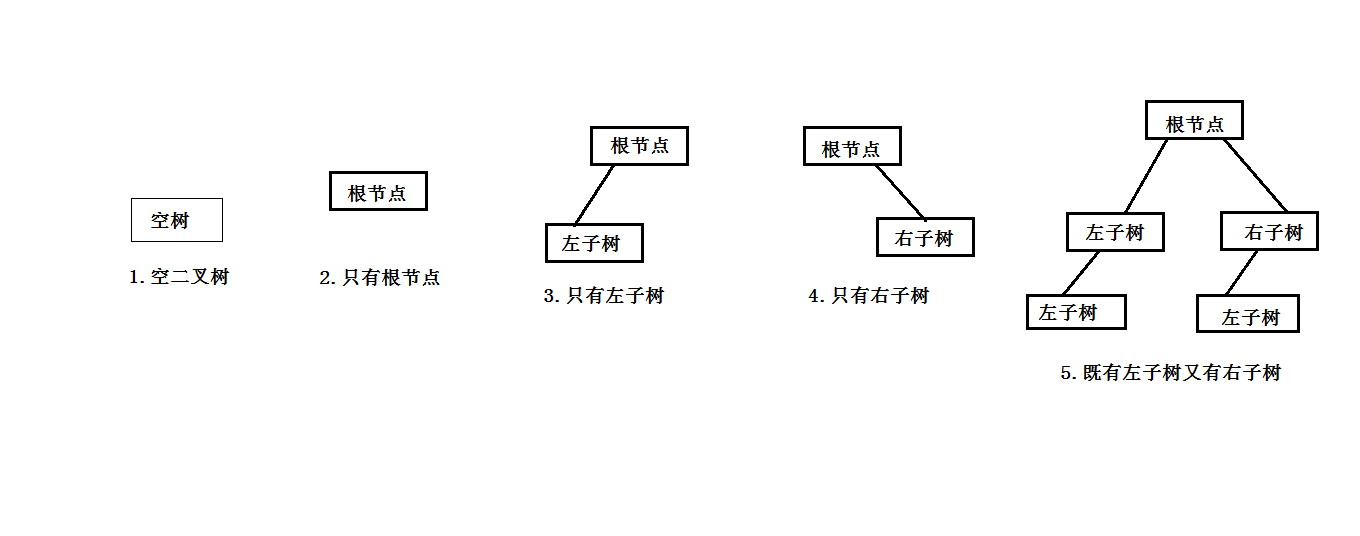
一棵二叉樹時節點的有限集合,該二叉樹或者為空樹、或者為只有一個根節點的樹、或者為一個根節點有左右子樹的樹。總之,二叉樹的每個節點最多有兩個子樹。下面畫圖表示二叉樹的幾種情況:
2. 二叉樹的特點
(1)二叉樹是遞迴定義的;
(2)二叉樹的每個節點最多有兩個子樹即二叉樹的度均不大於2;
(3)二叉樹的子樹有左右之分,其左右子樹的次序不能顛倒。
3. 二叉樹的相關操作
首先,怎麼表示一棵樹呢?我們可以類似於連結串列的形式,將一個指標變數的指向表示一棵樹。然後,如何儲存二叉樹的節點呢?由於二叉樹的特點:每個節點最多隻有兩個子樹,故可以將二叉樹每個節點的結構體設定為存放當前節點的元素,以及當前節點的左右子樹的指向。依據這樣的分析,寫出關於二叉樹的標頭檔案tree.h如下:
//標頭檔案只被編譯一次 #pragma once //巨集定義一個識別符號,用於測試時列印函式名 #define HEADER printf("================%s===============\n",__FUNCTION__) //自定義樹節點的資料型別,方便使用者修改樹節點的資料型別,預設設定為char型別 typedef char TreeNodeType; //使用孩子表示法來表示樹節點 typedef struct TreeNode{ //儲存樹節點的元素 TreeNodeType data; //儲存樹節點的左子樹的指向 struct TreeNode* lchild; //儲存樹節點的右子樹的指向 struct TreeNode* rchild; }TreeNode;
3.1 二叉樹的初始化、銷燬節點、建立節點
初始化:既然是以一個指標變數的指向表示一棵二叉樹,那麼二叉樹的初始化即將指標變數的指向置為空,初始化為一棵空二叉樹。
//1.初始化 //思路:由於是使用根節點的指標表示一棵樹,所以將根節點的指標置為NULL即表示初始化二叉樹為空樹 void TreeInit(TreeNode** proot) { //非法判斷 if(proot==NULL) { return; } //將根節點的指標置為NULL *proot=NULL; }
銷燬節點:銷燬一個節點,相當於釋放掉申請的記憶體空間,即使用free即可。
//2.銷燬節點
//思路:直接將節點的指向釋放
void DestroyTreeNode(TreeNode* node)
{
free(node);
}建立節點:先申請一塊新記憶體,用於存放二叉樹節點資訊;再將節點的data域置為傳入的引數值;3.最後,由於不知道該節點的左右子樹是誰,所以暫且將該節點的左右子樹的指向置為空。
//3.建立節點
//思路:將元素值賦值給節點的data,並將節點的lchild和rchild置為NULL
TreeNode* CreateTreeNode(TreeNodeType value)
{
//動態申請新節點的記憶體
TreeNode* new_node=(TreeNode*)malloc(sizeof(TreeNode));
//給new_node的data賦值
new_node->data=value;
//給new_node的lchild和rchild置為NULL
new_node->lchild=NULL;
new_node->rchild=NULL;
//返回建立的新節點的指向
return new_node;
}3.2 關於二叉樹的遍歷:先序遍歷、中序遍歷、後序遍歷、層序遍歷
1.先序遍歷
遍歷的順序為根左右,具體操作分析如下:
(1)a這棵樹,先訪問根節點a,再訪問a的左子樹b(左邊紅色框內為a的左子樹)
(2)b這棵樹,先訪問根節點b,再訪問b的左子樹d(左邊綠色框內為b的左子樹)
(3)d這棵樹,先訪問根節點d,d沒有左右子樹,所以根據根左右順序,訪問b這棵樹的右子樹e(右邊綠色框內為b的右子樹)
(4)e這棵樹,先訪訪問根節點e,再訪問e的左子樹g(左邊紫色框內為e的左子樹)
(5)g這棵樹,先訪問根節點g,g沒有左右子樹,所以根據根左右順序,訪問a這棵樹的右子樹c(右邊紅色框內為a的右子樹)
(6)c這棵樹,先訪問根節點c,c沒有左子樹,所以根據根左右的順序,訪問c這棵樹的右子樹f(右邊藍色框內為c的右子樹)
(7)f這棵樹,先訪問根節點f,f沒有左右子樹,所以根據根左右順序,整個二叉樹訪問完畢!
故,先序遍歷的結果為:a b d e g c f
程式碼實現如下所示:
//思路:根左右的順序去訪問
//1.先訪問根節點
//2.遞迴遍歷左子樹
//3.遞迴遍歷右子樹
void TreePreOrder(TreeNode* root)
{
//空樹
if(root==NULL)
{
return;
}
//1.先訪問根節點
printf("%c ",root->data);
//2.遞迴遍歷左子樹
TreePreOrder(root->lchild);
//3.遞迴遍歷右子樹
TreePreOrder(root->rchild);
}2.中序遍歷
遍歷的順序為左根右,具體操作分析如下:
(1)a這棵樹,先訪問a的左子樹b(左邊紅色框內為a的左子樹b)
(2)b這棵樹,先訪問b的左子樹d(左邊綠色框內為b的左子樹d)
(3)d這棵樹,沒有左子樹,所以根據左根右順序,訪問d這棵樹的根節點d,又d沒有右子樹,所以再訪問b這棵樹
(4)b這棵樹,訪問過左子樹後,根據左根右順序,再訪問b這棵樹的根節點b,再訪問b的右子樹
(5)b這棵樹,訪問過左子樹和根節點後,根據左根右的順序,再訪問b這棵樹的右子樹e(右邊綠色框內為b的右子樹e)
(6)e這棵樹,先訪問e的左子樹g(左邊紫色框內為e的左子樹g)
(7)g這棵樹,由於沒有左子樹,根據左根右順序,訪問g的根節點g,又g也沒有右子樹,所以g訪問完了繼續訪問e這棵樹
(8)e這棵樹,訪問過e的左子樹,根據左根右順序,再訪問e的根節點e,又e沒有右子樹,所以e訪問完了繼續訪問b這棵樹,又由於b這棵樹也訪問完了,所以繼續訪問a這棵樹
(9)a這棵樹,訪問過a的左子樹,根據左根右順序,訪問a的根節點a,再訪問a的右子樹c(右邊紅色框內為a的右子樹c)
(10)c這棵樹,由於c沒有左子樹,根據左根右順序,所以訪問c的根節點c,再訪問c的右子樹f(右邊藍色框內為c的右子樹f)
(11)f這棵樹,由於沒有左子樹,根據左根右順序,所以訪問f的根節點f,又f也沒有右子樹,所以f訪問完了繼續訪問a這棵樹,又a這棵樹也訪問完了,所以整個二叉樹訪問完畢!
故,中序遍歷的結果為:d b g e a c f
程式碼實現如下所示:
//5.樹的中序遍歷
//思路:左根右的順序去訪問
//1.遞迴遍歷左子樹
//2.訪問根節點
//3.遞迴遍歷右子樹
void TreeInOrder(TreeNode* root)
{
//空樹
if(root==NULL)
{
return;
}
//1.遞迴遍歷左子樹
TreeInOrder(root->lchild);
//2.訪問根節點
printf("%c ",root->data);
//3.遞迴遍歷右子樹
TreeInOrder(root->rchild);
}3.後序遍歷
遍歷的順序為左右根,具體操作分析如下:
(1)a這棵樹,根據左右根順序,先訪問a的左子樹b(左邊紅色框內為a的左子樹b)
(2)b這棵樹,根據左右根順序,先訪問b的左子樹d(左邊綠色框內為b的左子樹d)
(3)d這棵樹,由於d沒有左右子樹,所以訪問d的根節點d,d訪問完了繼續訪問b這棵樹
(4)b這棵樹,由於訪問過b的左子樹,根據左右根,所以再訪問b的右子樹e(右邊綠色框內為b的右子樹e)
(5)e這棵樹,根據左右根順序,先訪問e的左子樹g(左邊紫色框內為e的左子樹g)
(6)g這棵樹,由於g沒有左右子樹,所以訪問g的根節點g,g訪問完了繼續訪問e這棵樹
(7)e這棵樹,根據左右根順序且e沒有右子樹,所以訪問e的根節點e,e訪問完了繼續訪問b這棵樹
(8)b這棵樹,訪問過了b的左右子樹,根據左右根順序,所以再訪問b的根節點b,b這棵樹訪問完了繼續訪問a這棵樹
(9)a這棵樹,訪問過了a的左子樹,根據左右根順序,再訪問a的右子樹c(右邊紅色框內為a的右子樹c)
(10)c這棵樹,由於c沒有左子樹,根據左右根順序,訪問c的右子樹f(右邊藍色框內為c的右子樹f)
(11)f這棵樹,由於f沒有左右子樹,根據左右根順序,所以訪問f的根節點f,f訪問完了繼續訪問c這棵樹
(12)c這棵樹,由於訪問完了c的左右子樹,根據左右根順序,再訪問c的根節點c,c訪問完了繼續訪問a這棵樹
(13)a這棵樹,由於訪問過了c的左右子樹,根據左右根順序,再訪問a的根節點a,a訪問完即整個二叉樹訪問完畢!
故,後序遍歷的結果為:d g e b f c a
程式碼實現如下所示:
//6.樹的後序遍歷
//思路:左右根的順序去訪問
//1.遞迴遍歷左子樹
//2.遞迴遍歷右子樹
//3.訪問根節點
void TreePostOrder(TreeNode* root)
{
//空樹
if(root==NULL)
{
return;
}
//1.遞迴遍歷左子樹
TreePostOrder(root->lchild);
//2.遞迴遍歷右子樹
TreePostOrder(root->rchild);
//3.訪問根節點
printf("%c ",root->data);
}4.層序遍歷
遍歷的順序為一層一層的遍歷,具體操作分析如下:
(1)從左向右訪問第一層(紅色框內為第一層),故先訪問a
(2)從左向右訪問第二層(綠色框內為第二層),故再訪問b c
(3)從左向右訪問第三層(藍色框內為第三層),故再訪問d e f
(4)從左向右訪問第四層(紫色框內為第四層),故最後訪問g
故,層序遍歷的結果為:a b c d e f g
那程式碼實現要怎麼實現呢?僅僅通過觀察層數來層序遍歷二叉樹是不能夠用程式碼實現的,我們可以利用佇列來幫助我們實現層序遍歷的程式碼。整體思路如下:
(1)既然要利用佇列,就會用到佇列的入佇列、出佇列、取隊首元素的操作
(2)首先,將二叉樹的根節點入佇列、取隊首元素並出佇列
(3)將出佇列的根節點的左右子樹依次入佇列
(4)取當前佇列的隊首元素並出佇列,再將出佇列的節點的左右子樹依次入佇列
(5)再迴圈執行第四步
//7.樹的層序遍歷
//思路:藉助佇列
//1.將根節點入佇列,取隊首元素並出佇列
//2.將1步中出佇列的節點的左右子樹入佇列,取隊首元素並出佇列
//3.將2步中出佇列的節點的左右子樹入佇列,取對手元素並出佇列
//4.如此反覆,總結為三步走戰略:1.節點入佇列 2.取隊首元素並出佇列 3.將出佇列的節點的左右子樹入佇列
void TreeLevelOrder(TreeNode* root)
{
//空樹
if(root==NULL)
{
return;
}
//建立佇列並初始化
SeqQueue queue;
SeqQueueInit(&queue);
//1.將根節點入佇列
SeqQueuePush(&queue,root);
//迴圈執行取隊首元素出佇列入佇列操作
while(1)
{
//2.取隊首元素
SeqQueueType front;
int ret=SeqQueueFront(&queue,&front);
//若取隊首元素失敗,則佇列為空;若佇列為空,則迴圈結束
if(ret==0)
{
return;
}
//3.列印當前隊首元素的data
printf("%c ",front->data);
//4.出佇列
SeqQueuePop(&queue);
//5.將出佇列的節點的左右子樹入佇列
if(front->lchild!=NULL)
{
SeqQueuePush(&queue,front->lchild);
}
if(front->rchild!=NULL)
{
SeqQueuePush(&queue,front->rchild);
}
}
}注:以上程式碼用到的關於佇列的相關操作,需要用到我的部落格:https://blog.csdn.net/tongxuexie/article/details/79858973中的關於順序表實現佇列的入佇列、出佇列、取隊首元素的操作!但需要注意的是,之前的佇列元素的資料型別為char,現在需要改為二叉樹節點的結構體型別TreeNode*。這裡就不再新增關於佇列的程式碼!自行修改實現!
3.3 建立二叉樹
要求:通過一個數組,該陣列中的元素內容符合二叉樹的先序遍歷後的結果,且該陣列中元素不僅僅有非空子樹的元素,還有空子樹的元素,而空子樹的元素是什麼可以自行定義,但不要和非空子樹的元素髮生衝突!
建立樹的思路如下:
(1)依然利用的是遞迴的思想建立二叉樹
(2)定義一個變數index,用於表示陣列索引值,遞迴時,通過傳入index的地址去統一改變index的指向,從而訪問陣列的元素
(3)先根據index指向的內容,建立一棵樹
(4)再將index++,遞迴建立這棵樹的左子樹
(5)再將index++,遞迴建立這棵樹的右子樹
(6)遞迴執行第三、四、五步,從而利用一個數組建立一棵樹
(7)遞迴出口為index超出的陣列的大小size時,返回NULL
程式碼實現如下所示:
//8.建立樹
//思路:輸入一個數組,根據陣列的內容構建一棵樹,陣列中的元素符合樹的先序遍歷且包括空子樹
//傳入三個引數:1.陣列 2.陣列的大小 3.設定空子樹的元素
//1.index表示陣列的索引值,根據index指向的內容,建立一棵樹
//2.index++後遞迴建立新節點的左子樹
//3.index++後遞迴建立新節點的右子樹
TreeNode* CreateTree(TreeNodeType data[],size_t size,TreeNodeType null_type)
{
//定義變數,表示陣列的索引值
int index=0;
//傳入index的地址,便於統一使用訪問陣列的索引值index
return _CreateTree(data,size,&index,null_type);
}
TreeNode* _CreateTree(TreeNodeType data[],size_t size,int* index,TreeNodeType null_type)
{
//非法輸入
if(index==NULL)
{
return NULL;
}
//*index是否超出陣列的合法範圍
if(*index>=size)
{
return NULL;
}
//當索引值為*index的陣列元素為空子樹時,返回NULL
if(data[*index]==null_type)
{
return NULL;
}
//1.建立根節點
TreeNode* new_node=CreateTreeNode(data[*index]);
//2.遞迴建立左子樹
++(*index);
new_node->lchild=_CreateTree(data,size,index,null_type);
//3.遞迴建立右子樹
++(*index);
new_node->rchild=_CreateTree(data,size,index,null_type);
return new_node;
}3.4 二叉樹的拷貝與銷燬
拷貝分為三種拷貝方式:1.淺拷貝 2.深拷貝 3.寫時拷貝。下面以深拷貝的方式對二叉樹進行拷貝
//9.樹的拷貝
//思路:採用的是深拷貝,即重新分配記憶體
TreeNode* TreeClone(TreeNode* root)
{
//空樹時返回NULL
if(root==NULL)
{
return NULL;
}
//按照先序方式進行遍歷
TreeNode* new_node=CreateTreeNode(root->data);
new_node->lchild=TreeClone(root->lchild);
new_node->rchild=TreeClone(root->rchild);
return new_node;
}銷燬的核心思想還是遍歷,所以用什麼方式遍歷去銷燬二叉樹很重要!!!
(1)選擇先序遍歷去銷燬二叉樹時,需要注意,當你銷燬了根節點後,需要知道根節點的左右子樹後才能接著銷燬二叉樹的其他節點,所以要想用先序遍歷的方式銷燬二叉樹,在銷燬每一個節點前,需要先將節點的左右子樹的指向儲存。
(2)選擇中序遍歷去銷燬二叉樹的思想和上述一樣。
(3)選擇後序遍歷銷燬二叉樹時,不需要另外儲存節點的左右子樹的指向,因為後序遍歷的順序是左右根,所以最後才會銷燬根節點。
我選擇利用後序遍歷實現銷燬二叉樹,程式碼實現如下所示:
//10.樹的銷燬
//後序遍歷去銷燬樹的每一個節點
void DestroyTree(TreeNode** proot)
{
//非法輸入
if(proot==NULL)
{
return;
}
//空樹
if(*proot==NULL)
{
return;
}
//1.銷燬左子樹
DestroyTree(&((*proot)->lchild));
//銷燬右子樹
DestroyTree(&((*proot)->rchild));
//銷燬當前根節點
DestroyTreeNode(*proot);
(*proot)=NULL;
}3.5 關於二叉樹的其他操作(程式碼中有詳細的思路以供參考)
//11.求二叉樹中節點個數
//思路1:利用計數器,每當遍歷到一個節點,就對計數器++
size_t TreeSize(TreeNode* root)
{
//定義計數器
size_t size=0;
//呼叫下面函式實現計數器++
_TreeSize(root,&size);
return size;
}
void _TreeSize(TreeNode* root,size_t* size)
{
if(root==NULL)
{
return;
}
++(*size);
_TreeSize(root->lchild,size);
_TreeSize(root->rchild,size);
}
//思路2:利用遞迴計算節點個數
size_t TreeSizeEx(TreeNode* root)
{
//空樹
if(root==NULL)
{
return 0;
}
return 1+TreeSizeEx(root->lchild)+TreeSizeEx(root->rchild);
}
//12.求二叉樹葉子節點個數
//利用遞迴,計算二叉樹葉子結點個數相當於計算二叉樹根節點的左右子樹的葉子結點個數的和
size_t TreeLeafSize(TreeNode* root)
{
//空樹
if(root==NULL)
{
return 0;
}
//左右子樹都為空時,該節點為葉子節點
if(root->lchild==NULL&&root->rchild==NULL)
{
return 1;
}
return TreeLeafSize(root->lchild)+TreeLeafSize(root->rchild);
}
//13.二叉樹的第K層節點個數
//思路:遞迴思想 => 計算二叉樹的第K層節點個數=1+二叉樹的根節點的左子樹的第K-1層節點個數+二叉樹的根節點的右子樹的第K-1層節點個數
size_t TreeKLevelSize(TreeNode* root,int k)
{
//空樹或者k不是合法範圍時
if(root==NULL||k<1)
{
return 0;
}
if(k==1)
{
return 1;
}
return TreeKLevelSize(root->lchild,k-1)+TreeKLevelSize(root->rchild,k-1);
}
//14.求二叉樹的高度
//遞迴思想 => 計算二叉樹的高度=1+二叉樹根節點的左子樹的高度+二叉樹根節點的右子樹的高度,遞迴下去
size_t TreeHeight(TreeNode* root)
{
if(root==NULL)
{
return 0;
}
//當節點的左右子樹為空時,高度+1
if(root->lchild==NULL&&root->rchild==NULL)
{
return 1;
}
//遞迴計算左子樹的高度
size_t lheight=TreeHeight(root->lchild);
//遞迴計算右子樹的高度
size_t rheight=TreeHeight(root->rchild);
return 1+(lheight>rheight?lheight:rheight);
}
//15.在二叉樹中查詢節點
//思路:利用先序遍歷查詢節點
TreeNode* TreeFind(TreeNode* root,TreeNodeType to_find)
{
//空樹
if(root==NULL)
{
return NULL;
}
if(root->data==to_find)
{
return root;
}
//在根節點的左子樹中查詢
TreeNode* lresult=TreeFind(root->lchild,to_find);
//在根節點的右子樹中查詢
TreeNode* rresult=TreeFind(root->rchild,to_find);
//非空的子樹為要查詢的節點
return lresult!=NULL?lresult:rresult;
}
//16.求父節點
TreeNode* Parent(TreeNode* root,TreeNode* child)
{
//空樹或非法輸入
if(root==NULL||child==NULL)
{
return NULL;
}
//當節點的左子樹或右子樹==child時,即找到了父節點
if(root->lchild==child||root->rchild==child)
{
return root;
}
//在節點的左子樹中繼續尋找父節點
TreeNode* lresult=Parent(root->lchild,child);
//在節點的右子樹中繼續尋找父節點
TreeNode* rresult=Parent(root->rchild,child);
//非空的子樹為要查詢的父節點
return lresult!=NULL?lresult:rresult;
}
//17.求左子樹
TreeNode* LChild(TreeNode* root)
{
//空樹
if(root==NULL)
{
return NULL;
}
return root->lchild;
}
//18.求右子樹
TreeNode* RChild(TreeNode* root)
{
//空樹
if(root==NULL)
{
return NULL;
}
return root->rchild;
}