1 樹的廣度優先遍歷演算法
廣度優先遍歷演算法，又叫寬度優先遍歷，或橫向優先遍歷，是從根節點開始，沿著樹的寬度遍歷樹的節點。如果所有節點均被訪問，則演算法中止。

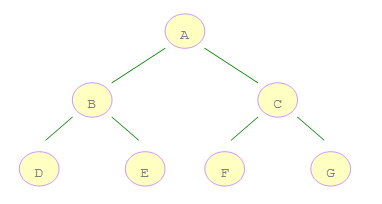
如上圖所示的二叉樹，A 是第一個訪問的，然後順序是 B、C，然後再是 D、E、F、G。
那麼，怎樣才能來保證這個訪問的順序呢？
藉助佇列資料結構，由於佇列是先進先出的順序，因此可以先將左子樹入隊，然後再將右子樹入隊。
這樣一來，左子樹結點就存在隊頭，可以先被訪問到。

//廣度優先遍歷

void breadthFirstTravel(Node* root){
queue<Node *> nodeQueue;  //使用C++的STL標準模板庫
 

    nodeQueue.push(root);
    Node *node;
    while(!nodeQueue.empty()){
        node = nodeQueue.front();
        nodeQueue.pop();
        printf(format, node->data);
        if(node->lchild){
            nodeQueue.push(node->lchild);  //先將左子樹入隊
        }
        if(node->rchild){
            nodeQueue.push(node->rchild);  //再將右子樹入隊
 

        }
    }
}

2 樹的深度優先遍歷演算法
深度優先遍歷演算法是遍歷演算法的一種。是沿著樹的深度遍歷樹的節點。

當節點v的所有邊都己被探尋過，搜尋將回溯到發現節點v的那條邊的起始節點。這一過程一直進行到已發現從源節點可達的所有節點為止。

如果還存在未被發現的節點，則選擇其中一個作為源節點並重復以上過程，整個程序反覆進行直到所有節點都被訪問為止。

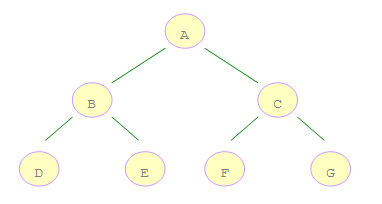
如上圖所示的二叉樹：

A 是第一個訪問的，然後順序是 B、D，然後是 E。接著再是 C、F、G。

那麼，怎麼樣才能來保證這個訪問的順序呢？

分析一下，在遍歷了根結點後，就開始遍歷左子樹，最後才是右子樹。

因此可以藉助堆疊的資料結構，由於堆疊是後進先出的順序，由此可以先將右子樹壓棧，然後再對左子樹壓棧，

這樣一來，左子樹結點就存在了棧頂上，因此某結點的左子樹能在它的右子樹遍歷之前被遍歷。

//深度優先遍歷

void depthFirstTravel(Node* root){
    stack<Node *> nodeStack;  //使用C++的STL標準模板庫
    nodeStack.push(root);
    Node *node;
    while(!nodeStack.empty()){
        node = nodeStack.top();
        printf(format, node->data);  //遍歷根結點
        nodeStack.pop();
        if(node->rchild){
            nodeStack.push(node->rchild);  //先將右子樹壓棧
        }
        if(node->lchild){
            nodeStack.push(node->lchild);  //再將左子樹壓棧
        }
    }
}