Prim演算法求解最小生成樹的Java實現
阿新 • • 發佈:2019-02-15
上一篇既然提到了Krusal演算法,這裡就不得不說Prim演算法了,這兩個演算法都是求解最小生成樹的經典的貪婪演算法。與Krusal演算法不同的是,Prim演算法在求解過程中始終保持臨時結果是一顆聯通的樹。該演算法的虛擬碼如下
//假設網路中至少有一個個頂點 設T為所選邊的集合,初始化T為空 設 TV為已在樹中的頂點的集合,置TV={1} 令E為網路中的邊的集合 while(E不為空,並且T 中的邊數不等於n-1){//這裡n指原圖中頂點個數 令(u,v)為最小代價的邊,其中u屬於TV,v不屬於TV if(沒有這種邊) break E=E-{(u,v)} 在T中加入邊(u,v) } if(|T|==n-1) T是一顆最小生成樹 else 沒有最小生成樹
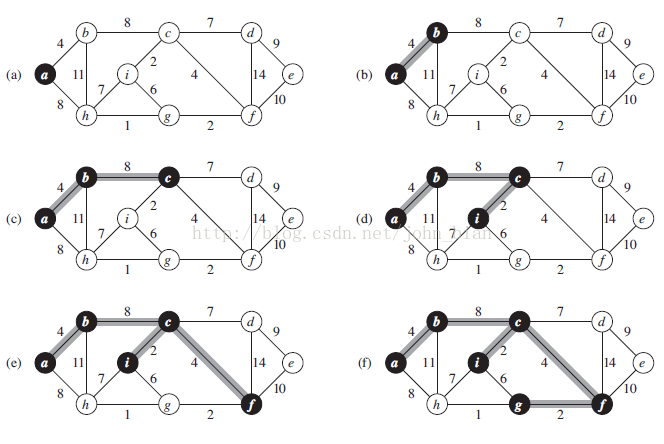
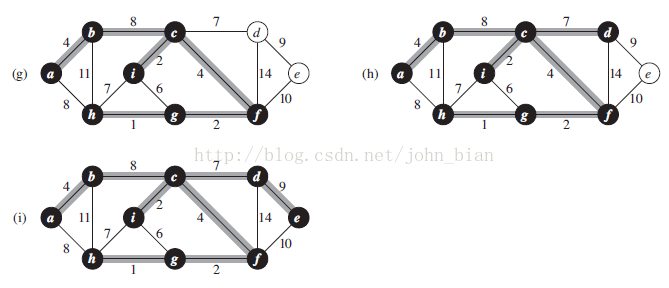
下圖是有一個Prim 演算法求解最小生成樹的過程的一個例子
以下是用Java程式碼點的實現
package Prim; /** * 邊 * @author sdu20 * */ public class Edge { private int v1; private int v2; private int weight; /** * 為查詢最小邊專門所設 * @param weight */ public Edge(int weight){ this.v1 = -1; this.v2 = -1; this.weight = weight; } public Edge(int v1,int v2,int weight){ this.v1 = v1; this.v2 = v2; this.weight = weight; } public int getV1(){ return v1; } public int getV2(){ return v2; } public int getWeight(){ return weight; } public String toString(){ String str = "[ "+v1+" , "+v2+" , "+weight+" ]"; return str; } public boolean equals(Edge edge){ boolean equal = this.v1==edge.getV1() && this.v2==edge.getV2() && this.weight==edge.getWeight() || this.v1==edge.getV2() && this.v2==edge.getV1() && this.weight==edge.getWeight(); return equal; } }
package Prim; import java.util.*; public class Graph { private int vNum; private int edgeNum; private LinkedList<Edge>[] edgeLinks; private LinkedList<Integer> TV; //已在樹中的頂點集 private LinkedList<Edge> T; //入選的邊集 public Graph(int vNum){ this.vNum = vNum; this.edgeNum = 0; edgeLinks = new LinkedList[vNum]; for(int i = 0;i<vNum;i++){ edgeLinks[i] = new LinkedList<>(); } } public void insertEdge(Edge edge){ int v1 = edge.getV1(); int v2 = edge.getV2(); edgeLinks[v1].add(edge); Edge edge2 = new Edge(v2,v1,edge.getWeight()); edgeLinks[v2].add(edge2); edgeNum++; } public void deleteEdge(Edge edge){ int v1 = edge.getV1(); int v2 = edge.getV2(); Edge edge2 = new Edge(v2,v1,edge.getWeight()); edgeLinks[v1].remove(edge); edgeLinks[v2].remove(edge2); edgeNum--; } public void bianli(){ System.out.println("共有 "+vNum+" 個頂點, "+edgeNum+" 條邊。"); for(int i = 0;i<vNum;i++){ LinkedList<Edge> list = (LinkedList<Edge>) edgeLinks[i].clone(); System.out.print(i+" : ["); while(!list.isEmpty()){ Edge edge = list.pop(); System.out.print(edge.getV2()+"("+edge.getWeight()+")"+" "); } System.out.println("]"); } } /** * Prim演算法實現 */ public void Prim(){ TV = new LinkedList<>(); T = new LinkedList<>(); TV.add(0); while(edgeNum>0 && T.size()!=vNum-1){ Edge edge = getMinEdge(TV); if(edge==null) break; this.deleteEdge(edge); T.add(edge); TV.add(edge.getV2()); } if(T.size()==vNum-1){ System.out.println("求最小生成樹成功"); LinkedList<Edge> list = (LinkedList<Edge>) T.clone(); int sumWeight = 0; while(!list.isEmpty()){ Edge edge = list.pop(); sumWeight += edge.getWeight(); System.out.println(edge.toString()); } System.out.println("總的權重為: "+sumWeight); }else{ System.out.println("無最小生成樹"); } } public Edge getMinEdge(LinkedList<Integer> t){ Edge minEdge = new Edge(10000); LinkedList<Integer> tt = (LinkedList<Integer>) t.clone(); while(!tt.isEmpty()){ int i = tt.pop(); LinkedList<Edge> list = (LinkedList<Edge>) edgeLinks[i].clone(); while(!list.isEmpty()){ Edge edge = list.pop(); if(minEdge.getWeight()>edge.getWeight() && !t.contains(edge.getV2())){ minEdge = edge; } } } if(minEdge.getWeight()==10000) return null; return minEdge; } }
package Prim;
public class Main {
public static void main(String[] args) {
// TODO Auto-generated method stub
bookGraph();
//randomGraph();
}
public static void bookGraph(){
Graph graph = new Graph(9);
Edge[] edges = new Edge[14];
edges[0] = new Edge(0,1,4);
edges[1] = new Edge(0,7,8);
edges[2] = new Edge(1,2,8);
edges[3] = new Edge(1,7,11);
edges[4] = new Edge(2,3,7);
edges[5] = new Edge(2,5,4);
edges[6] = new Edge(2,8,2);
edges[7] = new Edge(3,4,9);
edges[8] = new Edge(3,5,14);
edges[9] = new Edge(4,5,10);
edges[10] = new Edge(5,6,2);
edges[11] = new Edge(6,7,1);
edges[12] = new Edge(6,8,6);
edges[13] = new Edge(7,8,7);
for(int i = 0;i<14;i++){
graph.insertEdge(edges[i]);
}
graph.bianli();
graph.Prim();
}
/**
* 100個點,1000條邊,權重為1~100的隨機數
*/
public static void randomGraph(){
Graph graph = new Graph(100);
for(int i = 0;i<1000;){
int preV = (int)(Math.random()*100);
int folV = (int)(Math.random()*100);
int weight = (int)(Math.random()*100+1);
if(preV != folV){
Edge edge = new Edge(preV,folV,weight);
try{
graph.insertEdge(edge);
i++;
}catch(Exception e){
continue;
}
}
}
graph.bianli();
graph.Prim();
}
}
執行截圖如下所示