迴歸問題的條件/前提：

1） 收集的資料

2） 假設的模型，即一個函式，這個函式裡含有未知的引數，通過學習，可以估計出引數。然後利用這個模型去預測/分類新的資料。

1. 線性迴歸

假設 特徵 和 結果 都滿足線性。即不大於一次方。這個是針對 收集的資料而言。
收集的資料中，每一個分量，就可以看做一個特徵資料。每個特徵至少對應一個未知的引數。這樣就形成了一個線性模型函式，向量表示形式：

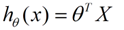
這個就是一個組合問題，已知一些資料，如何求裡面的未知引數，給出一個最優解。 一個線性矩陣方程，直接求解，很可能無法直接求解。有唯一解的資料集，微乎其微。

基本上都是解不存在的超定方程組。因此，需要退一步，將引數求解問題，轉化為求最小誤差問題，求出一個最接近的解，這就是一個鬆弛求解。

求一個最接近解，直觀上，就能想到，誤差最小的表達形式。仍然是一個含未知引數的線性模型，一堆觀測資料，其模型與資料的誤差最小的形式，模型與資料差的平方和最小：

這就是損失函式的來源。接下來，就是求解這個函式的方法，有最小二乘法，梯度下降法。

http://zh.wikipedia.org/wiki/%E7%BA%BF%E6%80%A7%E6%96%B9%E7%A8%8B%E7%BB%84

最小二乘法

是一個直接的數學求解公式，不過它要求X是列滿秩的，

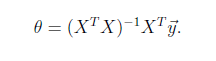
梯度下降法

分別有梯度下降法，批梯度下降法，增量梯度下降。本質上，都是偏導數，步長/最佳學習率，更新，收斂的問題。這個演算法只是最優化原理中的一個普通的方法，可以結合最優化原理來學，就容易理解了。

2. 邏輯迴歸

邏輯迴歸與線性迴歸的聯絡、異同？

邏輯迴歸的模型 是一個非線性模型，sigmoid函式，又稱邏輯迴歸函式。但是它本質上又是一個線性迴歸模型，因為除去sigmoid對映函式關係，其他的步驟，演算法都是線性迴歸的。可以說，邏輯迴歸，都是以線性迴歸為理論支援的。

只不過，線性模型，無法做到sigmoid的非線性形式，sigmoid可以輕鬆處理0/1分類問題。

另外它的推導含義：仍然與線性迴歸的最大似然估計推導相同，最大似然函式連續積（這裡的分佈，可以使伯努利分佈，或泊松分佈等其他分佈形式），求導，得損失函式。

邏輯迴歸函式

  表現了0,1分類的形式。

應用舉例：

是否垃圾郵件分類？

是否腫瘤、癌症診斷？

是否金融欺詐？

3. 一般線性迴歸

線性迴歸 是以 高斯分佈 為誤差分析模型； 邏輯迴歸 採用的是 伯努利分佈 分析誤差。

而高斯分佈、伯努利分佈、貝塔分佈、迪特里特分佈，都屬於指數分佈。

而一般線性迴歸，在x條件下，y的概率分佈 p(y|x) 就是指 指數分佈.

經歷最大似然估計的推導，就能匯出一般線性迴歸的 誤差分析模型（最小化誤差模型）。

softmax迴歸就是 一般線性迴歸的一個例子。

有監督學習迴歸，針對多類問題（邏輯迴歸，解決的是二類劃分問題），如數字字元的分類問題，0-9,10個數字，y值有10個可能性。

而這種可能的分佈，是一種指數分佈。而且所有可能的和 為1，則對於一個輸入的結果，其結果可表示為：

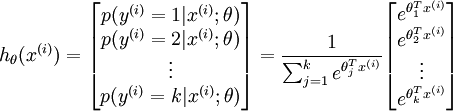引數是一個k維的向量。 而代價函式：

而對於softmax的求解，沒有閉式解法（高階多項方程組求解），仍用梯度下降法，或L-BFGS求解。

當k=2時，softmax退化為邏輯迴歸，這也能反映softmax迴歸是邏輯迴歸的推廣。

線性迴歸，邏輯迴歸，softmax迴歸 三者聯絡，需要反覆回味，想的多了，理解就能深入了。

4. 擬合：擬合模型/函式

由測量的資料，估計一個假定的模型/函式。如何擬合，擬合的模型是否合適？可分為以下三類

合適擬合

欠擬合

過擬合

看過一篇文章（附錄）的圖示，理解起來很不錯：

 欠擬合：

合適的擬合

過擬合

過擬合的問題如何解決？

問題起源？模型太複雜，引數過多，特徵數目過多。

方法： 1） 減少特徵的數量，有人工選擇，或者採用模型選擇演算法

http://www.cnblogs.com/heaad/archive/2011/01/02/1924088.html （特徵選擇演算法的綜述）

     2） 正則化，即保留所有特徵，但降低引數的值的影響。正則化的優點是，特徵很多時，每個特徵都會有一個合適的影響因子。

5. 概率解釋：線性迴歸中為什麼選用平方和作為誤差函式？

假設模型結果與測量值 誤差滿足，均值為0的高斯分佈，即正態分佈。這個假設是靠譜的，符合一般客觀統計規律。

資料x與y的條件概率：

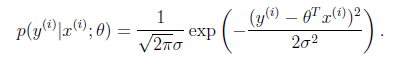
若使 模型與測量資料最接近，那麼其概率積就最大。概率積，就是概率密度函式的連續積，這樣，就形成了一個最大似然函式估計。對最大似然函式估計進行推導，就得出了求導後結果： 平方和最小公式

6. 引數估計 與 資料的關係

擬合關係

7. 錯誤函式/代價函式/損失函式：

線性迴歸中採用平方和的形式，一般都是由模型條件概率的最大似然函式 概率積最大值，求導，推匯出來的。

統計學中，損失函式一般有以下幾種：

1） 0-1損失函式

L(Y,f(X))={1,0,Y≠f(X)Y=f(X)

2） 平方損失函式

L(Y,f(X))=(Y−f(X))2

3） 絕對損失函式

L(Y,f(X))=|Y−f(X)|

4） 對數損失函式

L(Y,P(Y|X))=−logP(Y|X)

損失函式越小，模型就越好，而且損失函式 儘量 是一個凸函式，便於收斂計算。

線性迴歸，採用的是平方損失函式。而邏輯迴歸採用的是 對數 損失函式。 這些僅僅是一些結果，沒有推導。

8. 正則化：

為防止過度擬合的模型出現（過於複雜的模型），在損失函式裡增加一個每個特徵的懲罰因子。這個就是正則化。如正則化的線性迴歸 的 損失函式：

lambda就是懲罰因子。

正則化是模型處理的典型方法。也是結構風險最小的策略。在經驗風險（誤差平方和）的基礎上，增加一個懲罰項/正則化項。

線性迴歸的解，也從

θ=(XTX)−1XTy

轉化為

括號內的矩陣，即使在樣本數小於特徵數的情況下，也是可逆的。

邏輯迴歸的正則化：

從貝葉斯估計來看，正則化項對應模型的先驗概率，複雜模型有較大先驗概率，簡單模型具有較小先驗概率。這個裡面又有幾個概念。

什麼是結構風險最小化？先驗概率？模型簡單與否與先驗概率的關係？

經驗風險、期望風險、經驗損失、結構風險

期望風險（真實風險），可理解為 模型函式固定時，資料 平均的 損失程度，或“平均”犯錯誤的程度。 期望風險是依賴損失函式和概率分佈的。

只有樣本，是無法計算期望風險的。

所以，採用經驗風險，對期望風險進行估計，並設計學習演算法，使其最小化。即經驗風險最小化（Empirical Risk Minimization）ERM，而經驗風險是用損失函式來評估的、計算的。

對於分類問題，經驗風險，就訓練樣本錯誤率。

對於函式逼近，擬合問題，經驗風險，就平方訓練誤差。

對於概率密度估計問題，ERM，就是最大似然估計法。

而經驗風險最小，並不一定就是期望風險最小，無理論依據。只有樣本無限大時，經驗風險就逼近了期望風險。

如何解決這個問題？ 統計學習理論SLT，支援向量機SVM就是專門解決這個問題的。

有限樣本條件下，學習出一個較好的模型。

由於有限樣本下，經驗風險Remp[f]無法近似期望風險R[f] 。因此，統計學習理論給出了二者之間的關係：R[f] <= ( Remp[f] + e )

而右端的表達形式就是結構風險，是期望風險的上界。而e = g(h/n)是置信區間，是VC維h的增函式，也是樣本數n的減函式。

VC維的定義在 SVM，SLT中有詳細介紹。e依賴h和n，若使期望風險最小，只需關心其上界最小，即e最小化。所以，需要選擇合適的h和n。這就是結構風險最小化Structure Risk Minimization，SRM.

SVM就是SRM的近似實現，SVM中的概念另有一大筐。就此打住。

1範數，2範數 的物理意義：

範數，能將一個事物，對映到非負實數，且滿足非負性，齊次性，三角不等式。是一個具有“長度”概念的函式。

1範數為什麼能得到稀疏解？

壓縮感知理論，求解與重構，求解一個L1範數正則化的最小二乘問題。其解正是 欠定線性系統的解。

2範數為什麼能得到最大間隔解？

2範數代表能量的度量單位，用來重構誤差。

以上幾個概念理解需要補充。

9. 最小描述長度準則：

即一組例項資料，儲存時，利用一模型，編碼壓縮。模型長度，加上壓縮後長度，即為該資料的總的描述長度。最小描述長度準則，就是選擇 總的描述長度最小的模型。

最小描述長度MDL準則，一個重要特性就是避免過度擬合現象。

如利用貝葉斯網路，壓縮資料，一方面， 模型自身描述長度 隨模型複雜度的增加而增加 ； 另一方面， 對資料集描述的長度隨模型複雜度的增加而下降。因此， 貝葉斯網路的 MD L總是力求在模型精度和模型複雜度之間找到平衡。當模型過於複雜時，最小描述長度準則就會其作用，限制複雜程度。

奧卡姆剃刀原則：

如果你有兩個原理，它們都能解釋觀測到的事實，那麼你應該使用簡單的那個，直到發現更多的證據。

   萬事萬物應該儘量簡單，而不是更簡單。

11. 凸鬆弛技術：

將組合優化問題，轉化為易於求解極值點的凸優化技術。凸函式/代價函式的推導，最大似然估計法。

12. 牛頓法求解 最大似然估計

前提條件：求導迭代，似然函式可導，且二階可導。

迭代公式：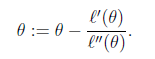

若是 向量形式，

H就是 n*n 的hessian矩陣了。

特徵：當靠近極值點時，牛頓法能快速收斂，而在遠離極值點的地方，牛頓法可能不收斂。 這個的推導？

這點是與梯度下降法的收斂特徵是相反的。

線性與非線性：

線性，一次函式；非線性，輸入、輸出不成正比，非一次函式。

線性的侷限性：xor問題。線性不可分，形式：

x  0

0  x

而線性可分，是隻用一個線性函式，將資料分類。線性函式，直線。

線性無關：各個獨立的特徵，獨立的分量，無法由其他分量或特徵線性表示。

核函式的物理意義：

對映到高維，使其變得線性可分。什麼是高維？如一個一維資料特徵x，轉換為（x，x^2, x^3），就成為了一個三維特徵，且線性無關。一個一維特徵線性不可分的特徵，在高維，就可能線性可分了。

邏輯迴歸logicalistic regression 本質上仍為線性迴歸，為什麼被單獨列為一類？

其存在一個非線性的對映關係，處理的一般是二元結構的0，1問題，是線性迴歸的擴充套件，應用廣泛，被單獨列為一類。

而且如果直接應用線性迴歸來擬合 邏輯迴歸資料，就會形成很多區域性最小值。是一個非凸集，而線性迴歸損失函式 是一個 凸函式，即最小極值點，即是全域性極小點。模型不符。

若採用 邏輯迴歸的 損失函式，損失函式就能形成一個 凸函式。

多項式樣條函式擬合

多項式擬合，模型是一個多項式形式；樣條函式，模型不僅連續，而且在邊界處，高階導數也是連續的。好處：是一條光滑的曲線，能避免邊界出現震盪的形式出現（龍格線性）
http://baike.baidu.com/view/301735.htm

以下是幾個需慢慢深入理解的概念：

無結構化預測模型

結構化預測模型

什麼是結構化問題？

adaboost， svm， lr 三個演算法的關係。

三種演算法的分佈對應 exponential loss（指數 損失函式）， hinge loss， log loss（對數損失函式）， 無本質區別。應用凸上界取代0、1損失，即凸鬆弛技術。從組合優化到凸集優化問題。凸函式，比較容易計算極值點。

正則化與貝葉斯引數估計的聯絡？

部分參考文章：

http://www.guzili.com/?p=45150

http://52opencourse.com/133/coursera%E5%85%AC%E5%BC%80%E8%AF%BE%E7%AC%94%E8%AE%B0-%E6%96%AF%E5%9D%A6%E7%A6%8F%E5%A4%A7%E5%AD%A6%E6%9C%BA%E5%99%A8%E5%AD%A6%E4%B9%A0%E7%AC%AC%E4%B8%83%E8%AF%BE-%E6%AD%A3%E5%88%99%E5%8C%96-regularization

http://www.cnblogs.com/jerrylead/archive/2011/03/05/1971867.html