2. 程式人生 > >TensorFlow入門：第一個機器學習Demo

TensorFlow入門：第一個機器學習Demo

阿新 • • 發佈：2019-02-15

本文主要通過一個簡單的 Demo 介紹 TensorFlow 初級 API 的使用方法，因為自己也是初學者，因此本文的目的主要是引導剛接觸 TensorFlow 或者 機器學習的同學，能夠從第一步開始學習 TensorFlow。閱讀本文先確認具備以下基礎技能：

  • 會使用 Python 程式設計（初級就OK，其實 TensorFlow 也支援 Java、C++、Go）
  • 一些陣列相關的知識（線性代數沒忘乾淨就行）
  • 最好再懂點機器學習相關的知識（臨時百度、Google也來得及）

基礎知識

張量（Tensor）

TensorFlow 內部的計算都是基於張量的，因此我們有必要先對張量有個認識。張量是在我們熟悉的標量、向量之上定義的，詳細的定義比較複雜，我們可以先簡單的將它理解為一個多維陣列：

3                                       # 這個 0 階張量就是標量，shape=[]
[1., 2., 3.]                            # 這個 1 階張量就是向量，shape=[3]
[[1., 2., 3.], [4., 5., 6.]]            # 這個 2 階張量就是二維陣列，shape=[2, 3]
[[[1., 2., 3.]], [[7., 8., 9.]]]        # 這個 3 階張量就是三維陣列，shape=[2, 1, 3]

TensorFlow 內部使用tf.Tensor

類的例項來表示張量，每個 tf.Tensor有兩個屬性：

  • dtype Tensor 儲存的資料的型別，可以為tf.float32、tf.int32、tf.string…
  • shape Tensor 儲存的多維陣列中每個維度的陣列中元素的個數，如上面例子中的shape

我們現在可以敲幾行程式碼看一下 Tensor 。在命令終端輸入 python 或者 python3 啟動一個 Python 會話，然後輸入下面的程式碼：

# 引入 tensorflow 模組
import tensorflow as tf

# 建立一個整型常量，即 0 階 Tensor
t0 = tf.constant(3
 
, dtype=tf.int32)

# 建立一個浮點數的一維陣列，即 1 階 Tensor
t1 = tf.constant([3., 4.1, 5.2], dtype=tf.float32)

# 建立一個字串的2x2陣列，即 2 階 Tensor
t2 = tf.constant([['Apple', 'Orange'], ['Potato', 'Tomato']], dtype=tf.string)

# 建立一個 2x3x1 陣列，即 3 階張量，資料型別預設為整型
t3 = tf.constant([[[5], [6], [7]], [[4], [3], [2]]])

# 列印上面建立的幾個 Tensor
print(t0)
print(t1)
print(t2)
print(t3)

上面程式碼的輸出為，注意shape的型別：

>>> print(t0)
Tensor("Const:0", shape=(), dtype=int32)
>>> print(t1)
Tensor("Const_1:0", shape=(3,), dtype=float32)
>>> print(t2)
Tensor("Const_2:0", shape=(2, 2), dtype=string)
>>> print(t3)
Tensor("Const_3:0", shape=(2, 3, 1), dtype=int32)

print 一個 Tensor 只能打印出它的屬性定義，並不能打印出它的值，要想檢視一個 Tensor 中的值還需要經過Session 執行一下：

>>> sess = tf.Session()
>>> print(sess.run(t0))
3
>>> print(sess.run(t1))
[ 3.          4.0999999   5.19999981]
>>> print(sess.run(t2))
[[b'Apple' b'Orange']
 [b'Potato' b'Tomato']]
>>> print(sess.run(t3))
[[[5]
  [6]
  [7]]

 [[4]
  [3]
  [2]]]
>>>

資料流圖(Dataflow Graph)

資料流是一種常用的平行計算程式設計模型，資料流圖是由節點(nodes)和線(edges)構成的有向圖：

  • 節點(nodes) 表示計算單元，也可以是輸入的起點或者輸出的終點
  • 線(edges) 表示節點之間的輸入/輸出關係

在 TensorFlow 中，每個節點都是用 tf.Tensor的例項來表示的，即每個節點的輸入、輸出都是Tensor，如下圖中 Tensor 在 Graph 中的流動，形象的展示 TensorFlow 名字的由來

TensorFlow 中的資料流圖有以下幾個優點：

  • 可並行 計算節點之間有明確的線進行連線，系統可以很容易的判斷出哪些計算操作可以並行執行
  • 可分發 圖中的各個節點可以分佈在不同的計算單元(CPU、 GPU、 TPU等)或者不同的機器中，每個節點產生的資料可以通過明確的線傳送的下一個節點中
  • 可優化 TensorFlow 中的 XLA 編譯器可以根據資料流圖進行程式碼優化，加快執行速度
  • 可移植 資料流圖的資訊可以不依賴程式碼進行儲存，如使用Python建立的圖，經過儲存後可以在C++或Java中使用

Sesssion

我們在Python中需要做一些計算操作時一般會使用NumPy，NumPy在做矩陣操作等複雜的計算的時候會使用其他語言(C/C++)來實現這些計算邏輯，來保證計算的高效性。但是頻繁的在多個程式語言間切換也會有一定的耗時，如果只是單機操作這些耗時可能會忽略不計，但是如果在分散式平行計算中，計算操作可能分佈在不同的CPU、GPU甚至不同的機器中，這些耗時可能會比較嚴重。
TensorFlow 底層是使用C++實現，這樣可以保證計算效率，並使用 tf.Session類來連線客戶端程式與C++執行時。上層的Python、Java等程式碼用來設計、定義模型，構建的Graph，最後通過tf.Session.run()方法傳遞給底層執行。

構建計算圖

上面介紹的是 TensorFlow 和 Graph 的概念，下面介紹怎麼用 Tensor 構建 Graph。
Tensor 即可以表示輸入、輸出的端點，還可以表示計算單元，如下的程式碼建立了對兩個 Tensor 執行 + 操作的 Tensor：

import tensorflow as tf
# 建立兩個常量節點
node1 = tf.constant(3.2)
node2 = tf.constant(4.8)
# 建立一個 adder 節點，對上面兩個節點執行 + 操作
adder = node1 + node2
# 列印一下 adder 節點
print(adder)
# 列印 adder 執行後的結果
sess = tf.Session()
print(sess.run(adder))

上面print的輸出為：

Tensor("add:0", shape=(), dtype=float32)
8.0

上面使用tf.constant()建立的 Tensor 都是常量，一旦建立後其中的值就不能改變了。有時我們還會需要從外部輸入資料，這時可以用tf.placeholder 建立佔位 Tensor，佔位 Tensor 的值可以在執行的時候輸入。如下就是建立佔位 Tensor 的例子：

import tensorflow as tf
# 建立兩個佔位 Tensor 節點
a = tf.placeholder(tf.float32)
b = tf.placeholder(tf.float32)
# 建立一個 adder 節點，對上面兩個節點執行 + 操作
adder_node = a + b
# 列印三個節點
print(a)
print(b)
print(adder)
# 執行一下，後面的 dict 引數是為佔位 Tensor 提供輸入資料
sess = tf.Session()
print(sess.run(adder, {a: 3, b: 4.5}))
print(sess.run(adder, {a: [1, 3], b: [2, 4]}))

上面程式碼的輸出為：

Tensor("Placeholder:0", dtype=float32)
Tensor("Placeholder_1:0", dtype=float32)
Tensor("add:0", dtype=float32)
7.5
[ 3.  7.]

我們還可以新增其他操作構建複雜的 Graph

# 新增×操作
add_and_triple = adder * 3.
print(sess.run(add_and_triple, {a: 3, b: 4.5}))

上面的輸出為

22.5

TensorFlow 應用例項

上面介紹了 TensorFlow 中的一些基本概念，下面我們通過一個小例子來了解一下怎麼使用 TensorFlow 進行機器學習。

建立模型(Model)

如下為我們進行某項實驗獲得的一些實驗資料：

輸入 輸出
1 4.8
2 8.5
3 10.4
6 21
8 25.3

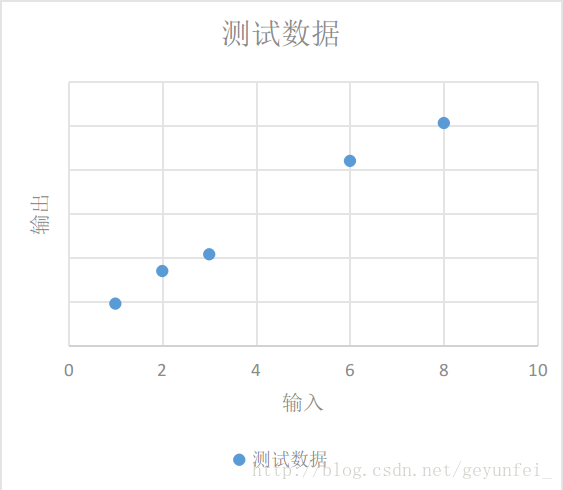
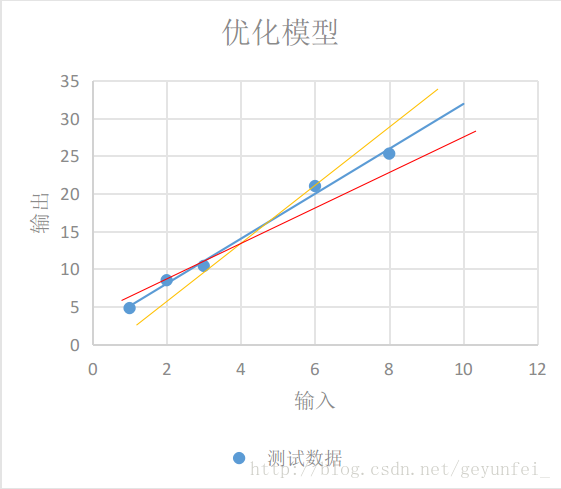
我們將這些資料放到一個二維圖上可以看的更直觀一些，如下，這些資料在圖中表現為一些離散的點：

我們需要根據現有的這些資料歸納出一個通用模型，通過這個模型我們可以預測其他的輸入值產生的輸出值。
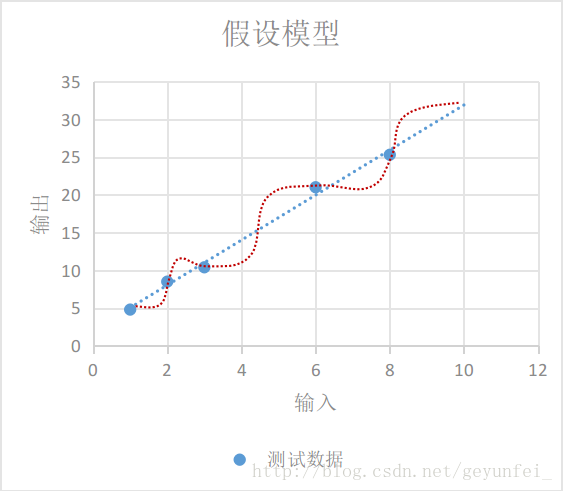
如下圖，我們選擇的模型既可以是紅線表示的鬼都看不懂的曲線模型，也可以是藍線表示的線性模型，在概率統計理論的分析中，這兩種模型符合真實模型的概率是一樣的。

根據 “奧卡姆剃刀原則-若有多個假設與觀察一致，則選最簡單的那個，藍線表示的線性模型更符合我們的直觀預期。
如果用 x 表示輸入， y 表示輸出，線性模型可以用下面的方程表示：

y=W×x+b
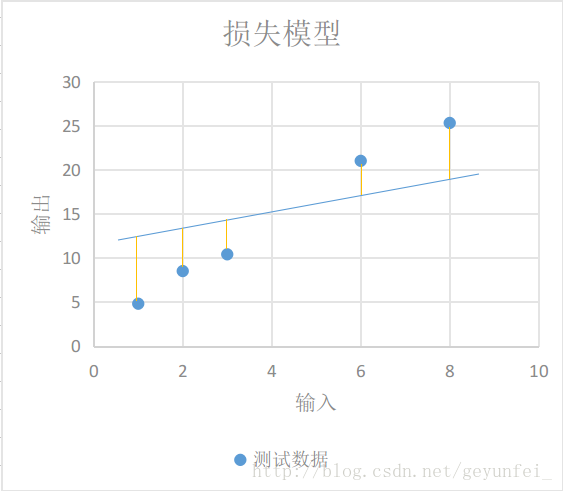
即使我們選擇了直線模型，可以選擇的模型也會有很多，如下圖的三條直線都像是一種比較合理的模型，只是W和b引數不同。這時我們需要設計一個損失模型(loss model)，來評估一下哪個模型更合理一些，並找到一個最準確的模型。

如下圖每條黃線代表線性模型計算出來的值與實際輸出值之間的差值:

我們用y′表示實驗得到的實際輸出，用下面的方程表示我們的損失模型：

loss=∑n=1N(yn−y′n)2

顯然，損失模型裡得到的loss越小，說明我們的線性模型越準確。

使用 TensorFlow 實現模型

上面我們根據實驗資料建立了一個線性模型，併為這個線性模型設計了一個損失模型，下面介紹的是怎麼在 TensorFlow 中實現我們設計的模型。
在我們的線性模型 y=W×x+b 中，輸入x可以用佔位 Tensor 表示，輸出y可以用線性模型的輸出表示，我們需要不斷的改變W和b的值，來找到一個使loss最小的值。這裡W和b可以用變數 Tensor 表示。使用tf.Variable()可以建立一個變數 Tensor，如下就是我們模型的實現程式碼：

import tensorflow as tf

# 建立變數 W 和 b 節點，並設定初始值
W = tf.Variable([.1], dtype=tf.float32)
b = tf.Variable([-.1], dtype=tf.float32)
# 建立 x 節點，用來輸入實驗中的輸入資料
x = tf.placeholder(tf.float32)
# 建立線性模型
linear_model = W*x + b

# 建立 y 節點，用來輸入實驗中得到的輸出資料，用於損失模型計算
y = tf.placeholder(tf.float32)
# 建立損失模型
loss = tf.reduce_sum(tf.square(linear_model - y))

# 建立 Session 用來計算模型
sess = tf.Session()

通過tf.Variable()建立變數 Tensor 時需要設定一個初始值，但這個初始值並不能立即使用，例如上面的程式碼中，我們使用print(sess.run(W))嘗試列印W的值會得到下面提示未初始化的異常

tensorflow.python.framework.errors_impl.FailedPreconditionError: Attempting to use uninitialized value Variable

變數 Tensor 需要經過下面的 init 過程後才能使用：

# 初始化變數
init = tf.global_variables_initializer()
sess.run(init)

這之後再使用print(sess.run(W))列印就可以看到我們之前賦的初始值：

[ 0.1]

變數初始化完之後，我們可以先用上面對W和b設定的初始值0.1和-0.1執行一下我們的線性模型看看結果：

print(sess.run(linear_model, {x: [1, 2, 3, 6, 8]}))

輸出結果為：

[ 0.          0.1         0.20000002  0.5         0.69999999]

貌似與我們實驗的實際輸出差距很大，我們再執行一下損失模型：

print(sess.run(loss, {x: [1, 2, 3, 6, 8], y: [4.8, 8.5, 10.4, 21.0, 25.3]}))

得到的損失值也很大

1223.05

我們可以用tf.assign()對W和b變數重新賦值再檢驗一下：

# 給 W 和 b 賦新值
fixW = tf.assign(W, [2.])
fixb = tf.assign(b, [1.])
# run 之後新值才會生效
sess.run([fixW, fixb])
# 重新驗證損失值
print(sess.run(loss, {x: [1, 2, 3, 6, 8], y: [4.8, 8.5, 10.4, 21.0, 25.3]}))

輸出的損失值比之前的小了很多：

159.94

我們需要不斷調整變數W和b的值，找到使損失值最小的W和b。這肯定是一個very boring的過程，因此 TensorFlow 提供了訓練模型的方法，自動幫我們進行這些繁瑣的訓練工作。

使用 TensorFlow 訓練模型

TensorFlow 提供了很多優化演算法來幫助我們訓練模型。最簡單的優化演算法是梯度下降(Gradient Descent)演算法，它通過不斷的改變模型中變數的值，來找到最小損失值。
如下的程式碼就是使用梯度下降優化演算法幫助我們訓練模型：

# 建立一個梯度下降優化器，學習率為0.001
optimizer = tf.train.GradientDescentOptimizer(0.001)
train = optimizer.minimize(loss)

# 用兩個陣列儲存訓練資料
x_train = [1, 2, 3, 6, 8]
y_train = [4.8, 8.5, 10.4, 21.0, 25.3]

# 訓練10000次
for i in range(10000):
    sess.run(train, {x: x_train, y: y_train})

# 列印一下訓練後的結果
print('W: %s b: %s loss: %s' % (sess.run(W), sess.run(b), sess.run(loss, {x: x_train , y: y_train})))

打印出來的訓練結果如下，可以看到損失值已經很小了：

W: [ 2.98236108] b: [ 2.07054377] loss: 2.12941

我們整理一下前面的程式碼，完整的demo程式碼如下，將下面的程式碼儲存在一個demo.py檔案裡，通過python3 demo.py執行一下就可以看到訓練結果了：

import tensorflow as tf

# 建立變數 W 和 b 節點，並設定初始值
W = tf.Variable([.1], dtype=tf.float32)
b = tf.Variable([-.1], dtype=tf.float32)
# 建立 x 節點，用來輸入實驗中的輸入資料
x = tf.placeholder(tf.float32)
# 建立線性模型
linear_model = W * x + b

# 建立 y 節點，用來輸入實驗中得到的輸出資料，用於損失模型計算
y = tf.placeholder(tf.float32)
# 建立損失模型
loss = tf.reduce_sum(tf.square(linear_model - y))

# 建立 Session 用來計算模型
sess = tf.Session()

# 初始化變數
init = tf.global_variables_initializer()
sess.run(init)

# 建立一個梯度下降優化器，學習率為0.001
optimizer = tf.train.GradientDescentOptimizer(0.001)
train = optimizer.minimize(loss)

# 用兩個陣列儲存訓練資料
x_train = [1, 2, 3, 6, 8]
y_train = [4.8, 8.5, 10.4, 21.0, 25.3]

# 訓練10000次
for i in range(10000):
    sess.run(train, {x: x_train, y: y_train})

# 列印一下訓練後的結果
print('W: %s b: %s loss: %s' % (sess.run(W), sess.run(
    b), sess.run(loss, {x: x_train, y: y_train})))

TensorFlow 高階訓練模型

tf.estimator是TensorFlow提供的高階庫，提供了很多常用的訓練模型，可以簡化機器學習中的很多訓練過程，如：

  • 執行訓練迴圈
  • 執行評估迴圈
  • 管理訓練資料集

評估模型

前面的demo中我們構建了一個線性模型，通過使用一組實驗資料訓練我們的線性模型，我們得到了一個自認為損失最小的最優模型，根據訓練結果我們的最優模型可以表示為下面的方程：

y=2.98x+2.07
但是這個我們自認為的最優模型是否會一直是最優的？我們需要通過一些新的實驗資料來評估(evaluation)模型的泛化效能(generalization performance)，如果新的實驗資料應用到到這個模型中損失值越小，那麼這個模型的泛化效能就越好，反之就越差。下面的demo中我們也會看到怎麼評估模型。

使用LinearRegressor

前面我們構建了一個線性模型，通過訓練得到一個線性迴歸方程。tf.estimator中也提供了線性迴歸的訓練模型tf.estimator.LinearRegressor，下面的程式碼就是使用LinearRegressor訓練並評估模型的方法：

# 我們會用到NumPy來處理各種訓練資料
import numpy as np
import tensorflow as tf

# 建立一個特徵向量列表，該特徵列表裡只有一個特徵向量，
# 該特徵向量為實數向量，只有一個元素的陣列，且該元素名稱為 x，
# 我們還可以建立其他更加複雜的特徵列表
feature_columns = [tf.feature_column.numeric_column("x", shape=[1])]

# 建立一個LinearRegressor訓練器，並傳入特徵向量列表
estimator = tf.estimator.LinearRegressor(feature_columns=feature_columns)

# 儲存訓練用的資料
x_train = np.array([1., 2., 3., 6., 8.])
y_train = np.array([4.8, 8.5, 10.4, 21.0, 25.3])

# 儲存評估用的資料
x_eavl = np.array([2., 5., 7., 9.])
y_eavl = np.array([7.6, 17.2, 23.6, 28.8])

# 用訓練資料建立一個輸入模型，用來進行後面的模型訓練
# 第一個引數用來作為線性迴歸模型的輸入資料
# 第二個引數用來作為線性迴歸模型損失模型的輸入
# 第三個引數batch_size表示每批訓練資料的個數
# 第四個引數num_epochs為epoch的次數，將訓練集的所有資料都訓練一遍為1次epoch
# 低五個引數shuffle為取訓練資料是順序取還是隨機取
train_input_fn = tf.estimator.inputs.numpy_input_fn(
    {"x": x_train}, y_train, batch_size=2, num_epochs=None, shuffle=True)

# 再用訓練資料建立一個輸入模型，用來進行後面的模型評估
train_input_fn_2 = tf.estimator.inputs.numpy_input_fn(
    {"x": x_train}, y_train, batch_size=2, num_epochs=1000, shuffle=False)

# 用評估資料建立一個輸入模型，用來進行後面的模型評估
eval_input_fn = tf.estimator.inputs.numpy_input_fn(
    {"x": x_eavl}, y_eavl, batch_size=2, num_epochs=1000, shuffle=False)

# 使用訓練資料訓練1000次
estimator.train(input_fn=train_input_fn, steps=1000)

# 使用原來訓練資料評估一下模型，目的是檢視訓練的結果
train_metrics = estimator.evaluate(input_fn=train_input_fn_2)
print("train metrics: %r" % train_metrics)

# 使用評估資料評估一下模型，目的是驗證模型的泛化效能
eval_metrics = estimator.evaluate(input_fn=eval_input_fn)
print("eval metrics: %s" % eval_metrics)

執行上面的程式碼輸出為：

train metrics: {'loss': 1.0493528, 'average_loss': 0.52467638, 'global_step': 1000}
eval metrics: {'loss': 0.72186172, 'average_loss': 0.36093086, 'global_step': 1000}

評估資料的loss比訓練資料還要小，說明我們的模型泛化效能很好。

自定義Estimator模型

tf.estimator庫中提供了很多預定義的訓練模型，但是有可能這些訓練模型不能滿足我們的需求，我們需要使用自己構建的模型。
我們可以通過實現tf.estimator.Estimator的子類來構建我們自己的訓練模型，LinearRegressor就是Estimator的一個子類。另外我們也可以只給Estimator基類提供一個model_fn的實現，定義我們自己的模型訓練、評估方法以及計算損失的方法。
下面的程式碼就是使用我們最開始構建的線性模型實現自定義Estimator的例項。

import numpy as np
import tensorflow as tf

# 定義模型訓練函式，同時也定義了特徵向量


def model_fn(features, labels, mode):
    # 構建線性模型
    W = tf.get_variable("W", [1], dtype=tf.float64)
    b = tf.get_variable("b", [1], dtype=tf.float64)
    y = W * features['x'] + b
    # 構建損失模型
    loss = tf.reduce_sum(tf.square(y - labels))
    # 訓練模型子圖
    global_step = tf.train.get_global_step()
    optimizer = tf.train.GradientDescentOptimizer(0.01)
    train = tf.group(optimizer.minimize(loss),
                     tf.assign_add(global_step, 1))
    # 通過EstimatorSpec指定我們的訓練子圖積極損失模型
    return tf.estimator.EstimatorSpec(
        mode=mode,
        predictions=y,
        loss=loss,
        train_op=train)

# 建立自定義的訓練模型
estimator = tf.estimator.Estimator(model_fn=model_fn)

# 後面的訓練邏輯與使用LinearRegressor一樣
x_train = np.array([1., 2., 3., 6., 8.])
y_train = np.array([4.8, 8.5, 10.4, 21.0, 25.3])

x_eavl = np.array([2., 5., 7., 9.])
y_eavl = np.array([7.6, 17.2, 23.6, 28.8])

train_input_fn = tf.estimator.inputs.numpy_input_fn(
    {"x": x_train}, y_train, batch_size=2, num_epochs=None, shuffle=True)

train_input_fn_2 = tf.estimator.inputs.numpy_input_fn(
    {"x": x_train}, y_train, batch_size=2, num_epochs=1000, shuffle=False)

eval_input_fn = tf.estimator.inputs.numpy_input_fn(
    {"x": x_eavl}, y_eavl, batch_size=2, num_epochs=1000, shuffle=False)

estimator.train(input_fn=train_input_fn, steps=1000)

train_metrics = estimator.evaluate(input_fn=train_input_fn_2)
print("train metrics: %r" % train_metrics)

eval_metrics = estimator.evaluate(input_fn=eval_input_fn)
print("eval metrics: %s" % eval_metrics)

上面程式碼的輸出為

train metrics: {'loss': 0.8984344, 'global_step': 1000}
eval metrics: {'loss': 0.48776609, 'global_step': 1000}

TensorBoard

為了更方便 TensorFlow 的建模和調優，Google 還為 TensorFlow 開發了一款視覺化的工具：TensorBoard，將我們第一個Demo的程式碼稍微改造一下，就可以使用 TensorBoard更加直觀的理解 TensorFlow 的訓練過程。

import tensorflow as tf

# 建立節點時設定name，方便在圖中識別
W = tf.Variable([0], dtype=tf.float32, name='W')
b = tf.Variable([0], dtype=tf.float32, name='b')

# 建立節點時設定name，方便在圖中識別
x = tf.placeholder(tf.float32, name='x')
y = tf.placeholder(tf.float32, name='y')

# 線性模型
linear_model = W * x + b

# 損失模型隱藏到loss-model模組
with tf.name_scope("loss-model"):
    loss = tf.reduce_sum(tf.square(linear_model - y))
    # 給損失模型的輸出新增scalar，用來觀察loss的收斂曲線
    tf.summary.scalar("loss", loss)

optmizer = tf.train.GradientDescentOptimizer(0.001)

train = optmizer.minimize(loss)

x_train = [1, 2, 3, 6, 8]
y_train = [4.8, 8.5, 10.4, 21.0, 25.3]


sess = tf.Session()
init = tf.global_variables_initializer()
sess.run(init)

# 呼叫 merge_all() 收集所有的操作資料
merged = tf.summary.merge_all()

# 模型執行產生的所有資料儲存到 /tmp/tensorflow 資料夾供 TensorBoard 使用
writer = tf.summary.FileWriter('/tmp/tensorflow', sess.graph)

# 訓練10000次
for i in range(10000):
    # 訓練時傳入merge
    summary, _ = sess.run([merged, train], {x: x_train, y: y_train})
    # 收集每次訓練產生的資料
    writer.add_summary(summary, i)

curr_W, curr_b, curr_loss = sess.run(
    [W, b, loss], {x: x_train, y: y_train})

print("After train W: %s b %s loss: %s" % (curr_W, curr_b, curr_loss))

執行完上面的程式碼後，訓練過程產生的資料就儲存在 /tmp/tensorflow 檔案夾了，我們可以在命令列終端執行下面的命令啟動 TensorBoard：

# 通過 --logdir 引數設定我們存放訓練資料的目錄
$ tensorboard --logdir /tmp/tensorflow

然後在瀏覽器中開啟 頁面就可以看到我們的模型資料了。
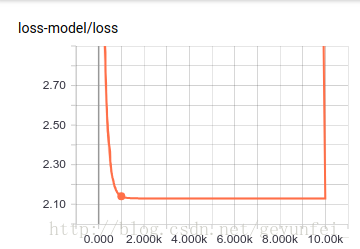
首先在 SCALARS 頁面我們可以看到我們通過 tf.summary.scalar("loss", loss)設定的loss收斂曲線，從曲線圖中可以看出在訓練了大概2000次的時候loss就已經收斂的差不多了。

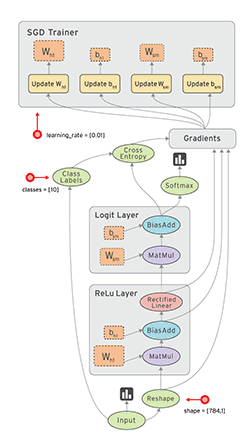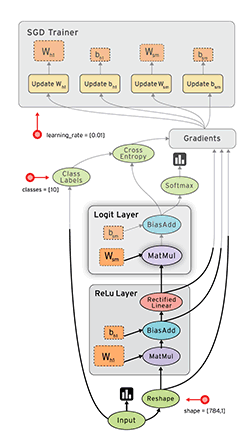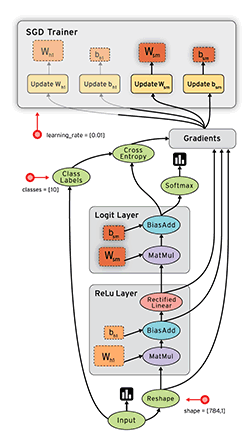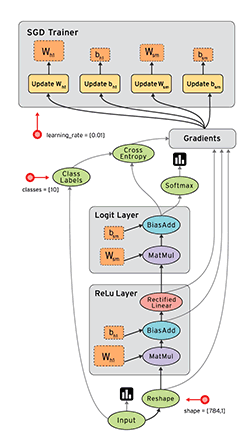
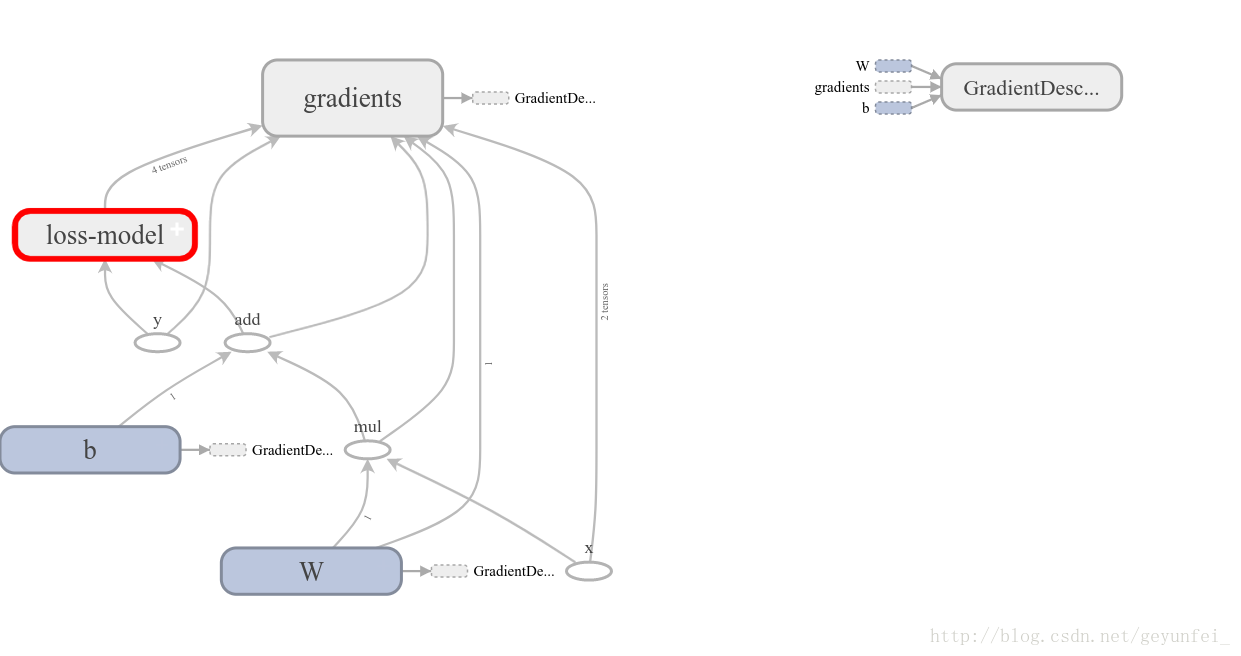
在 GRAPHS 頁面可以看到我們構建的模型的資料流圖：

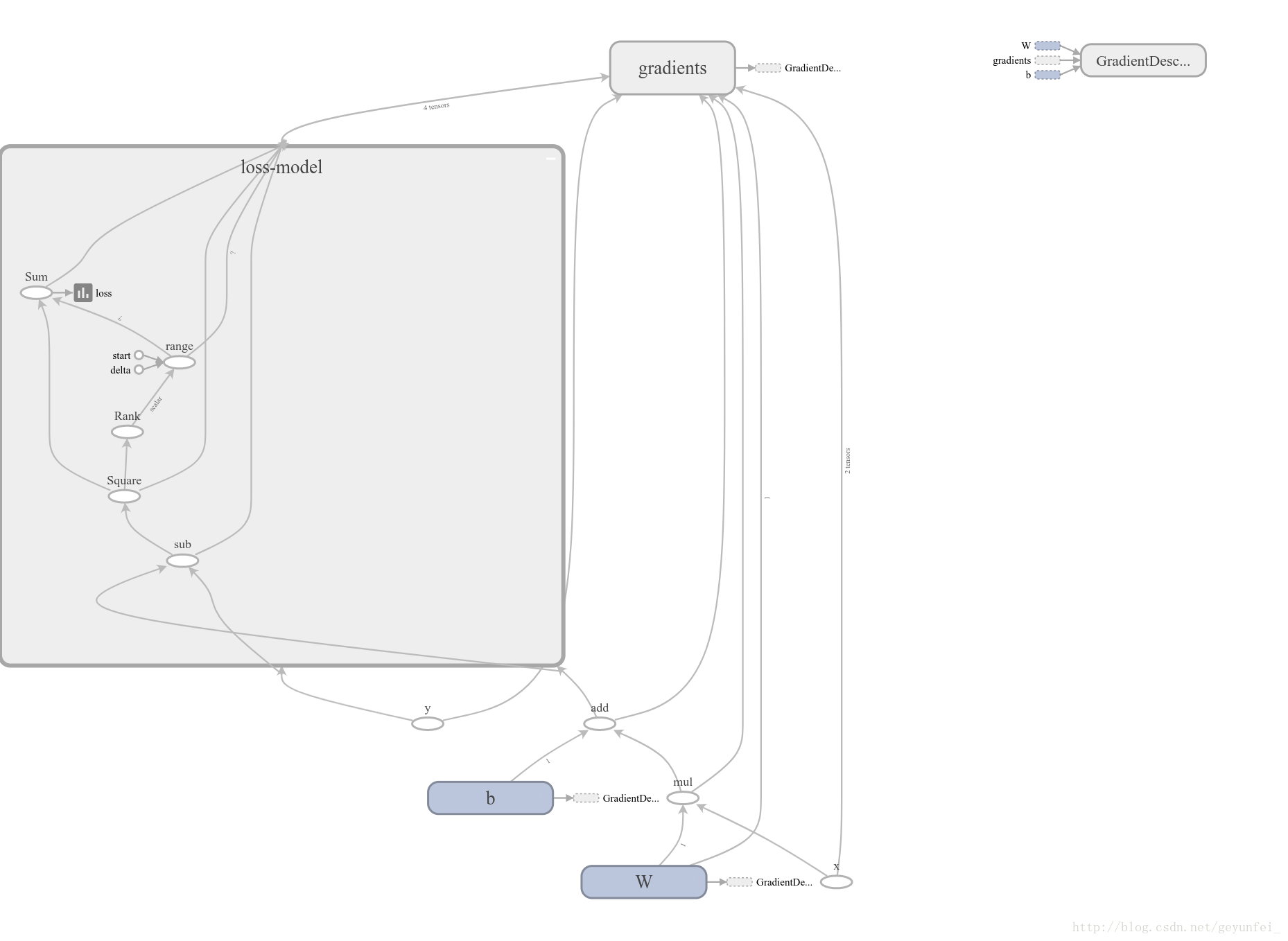
其中損失模型摺疊到loss-model模組裡了，雙擊該模組可以展開損失模型的內容：

– end –

如上即為本人初學 TensorFlow 時的入門 demo，如果想對 TensorFlow 有更深的瞭解可以參考如下網站：

相關推薦

TensorFlow入門：第一個機器學習Demo

本文主要通過一個簡單的 Demo 介紹 TensorFlow 初級 API 的使用方法，因為自己也是初學者，因此本文的目的主要是引導剛接觸 TensorFlow 或者 機器學習的同學，能夠從第一步開始學習 TensorFlow。閱讀本文先確認具備以下基礎技能：

TensorFlow入門之一：第一個機器學習Demo

版權宣告：本文為博主原創文章，未經博主允許不得轉載。 https://blog.csdn.net/geyunfei_/article/details/78782804 本文主要通過一個簡單的 Demo 介紹 TensorFlow 初級 API 的使用方法，因為自己也是初學者，因此本文的目

機器學習：用6行Python程式碼開始寫第一個機器學習程式

import sklearn from sklearn import tree # features = [[140, "smooth"],[130, "smooth"],[150, "bumpy"],[170,  "bumpy"]] # labels = ["apple",

第一個機器學習演算法：線性迴歸與梯度下降

# 第一個機器學習演算法：線性迴歸與梯度下降 ## 符號解釋 * $x^{(i)}$,$y^{(i)}$：某個訓練樣本 * $m$：樣本總數量 * $h_{\theta}$：假設函式 ## Linear regression（線性迴歸） ### 如何獲得一個線性迴歸模型？ * 將**訓練資料**放入

快應用入門：第一個快應用程式

簡介 快應用是九大手機廠商基於硬體平臺共同推出的新型應用生態，依附在各大應用市場。使用者無需下載安裝，即點即用，享受原生應用的效能體驗。2018年3月20日在北京推出“快應用”標準。該應用模組以標準js語法+重組css標籤+Flexbox佈局+mvvm模式。 第一

機器學習與深度學習系列連載： 第一部分 機器學習（五） 生成概率模型（Generative Model）

生成概率模型（Generative Model） 1.概率分佈 我們還是從分類問題說起： 當我們把問題問題看做是一個迴歸問題， 分類是class 1 的時候結果是1 分類為class 2的時候結果是-1； 測試的時候，結果接近1的是class1

機器學習與深度學習系列連載： 第一部分 機器學習（九）支援向量機2（Support Vector Machine）

另一種視角定義SVM：hinge Loss +kennel trick SVM 可以理解為就是hingle Loss和kernel 的組合 1. hinge Loss 還是讓我們回到二分類的問題，為了方便起見，我們y=1 看做是一類，y=-1 看做是另一類

機器學習與深度學習系列連載： 第一部分 機器學習（十一）決策樹2（Decision Tree）

決策樹2 決策樹很容易出現過擬合問題，針對過擬合問題，我們採用以下幾種方法 劃分選擇 vs 剪枝 剪枝 (pruning) 是決策樹對付“過擬合”的 主要手段！ 基本策略： 預剪枝 (pre-pruning): 提前終止某些分支的生長 後剪枝 (post-pr

機器學習與深度學習系列連載： 第一部分 機器學習（十三）半監督學習（semi-supervised learning）

在實際資料收集的過程中，帶標籤的資料遠遠少於未帶標籤的資料。 我們據需要用帶label 和不帶label的資料一起進行學習，我們稱作半監督學習。 Transductive learning：沒有標籤的資料是測試資料 Inductive learning：沒有標

機器學習與深度學習系列連載： 第一部分 機器學習（十四）非監督度學習-1 Unsupervised Learning-1

非監督度學習-1 Unsupervised Learning-1（K-means,HAC,PCA） 非監督學習方法主要分為兩大類 Dimension Reduction (化繁為簡) Generation （無中生有) 目前我們僅專注化繁為簡，降維的方法，

機器學習與深度學習系列連載： 第一部分 機器學習（十五）非監督度學習-2 Unsupervised Learning-2（Neighbor Embedding）

臨近編碼 Neighbor Embedding 在非監督學習降維演算法中，高緯度的資料，在他附近的資料我們可以看做是低緯度的，例如地球是三維度的，但是地圖可以是二維的。 那我們就開始上演算法 1. Locally Linear Embedding (LLE) 我

機器學習與深度學習系列連載： 第一部分 機器學習（十七）非監督度學習-2 Unsupervised Learning-4（Generative Models）

生成模型 Generative Models 用非監督學習生成結構化資料，是非監督模型的一個重要分支，本節重點介紹三個演算法： Pixel RNN ，VAE 和GAN（以後會重點講解原理） 1. Pixel RNN RNN目前還沒有介紹，，以後會重點講解，大家

爬蟲簡單入門：第一個簡單爬蟲

import requests # socket-->http-->requests response=requests.get('https://tieba.baidu.com/f?kw=%E6%B5%81%E6%B5%AA%E6%B1%89') print(response.text)

機器學習與深度學習系列連載： 第一部分 機器學習（十二）整合學習（Ensemble）

整合學習（Ensemble） 1. Bagging 我們考慮當結果的 variance 很大，如果降低 variance。 我們可以考慮“平行宇宙”，不同的training set 中生成不同的模型，然後做平均或者voting。 2. Decision Tre

機器學習與深度學習系列連載： 第一部分 機器學習（一）導論

什麼是機器學習？ 1.機器學習==尋找一種函式 這個函式可以： 語音識別:輸入一段語音訊號，輸出文字 ff()="howareyou"="howareyou" 影象識別:輸入圖片，輸出圖片的屬性 ff( )=“cat”=“cat” 智

機器學習與深度學習系列連載： 第一部分 機器學習（四）誤差分析（Bias and Variance）和模型調優

1.誤差分析（Bias and Variance） 當我們以非常複雜的模型去進行測試的時候，可能得到的結果並不理想 影響結果的主要有兩個因素：Bias 偏差、Variance 方差 Bias 偏差 在這裡，我們定義偏差是指與目標結果的偏移量，這個偏

機器學習與深度學習系列連載： 第一部分 機器學習（十八）模型評估

模型評估 模型評估中有三個關鍵問題：  如何獲得測試結果？ 評估方法  如何評估效能優劣？ 效能度量  如何判斷實質差別？ 比較檢驗 2. 效能度量(performance measure)是衡量模型泛化能力的 評價標準，反映了任務需求 （1

Unity入門：第一個遊戲

Unity官網提供了詳盡的文件和豐富的教學視訊，昨天跟著視訊做了一個簡單的3d遊戲“roll-a-ball”。遊戲涉及了許多Unity的基本知識，用來入門很不錯。 這篇博文並不講述整個遊戲的製作流程，如果您感興趣，可以訪問這裡，如果訪問遇到什麼困難，在B站有一摸一樣的視訊。

第002講：用Python設計第一個遊戲|學習記錄（小甲魚零基礎入門學習Python）

（標答出處: 魚C論壇） 《零基礎入門學習Python》 測試題： 什麼是BIF？ BIF指的是bulit in function，指的是Python裡的內建函式。 用課堂上小甲魚教的方法數一數 Python3 提供了多少個 BIF？ 輸入&g

ArcGIS API for JavaScript學習（1）：第一個地圖

樣式表 參數 資源 charset 底層 arcgis 順序 api navi 1.簡介 ArcGIS API for JavaScript跟隨ArcGIS 9.3同時發布，是ESRI根據JavaScript技術實現的調用ArcGIS Server REST API接口的一