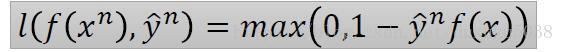機器學習與深度學習系列連載: 第一部分 機器學習(九)支援向量機2(Support Vector Machine)
阿新 • • 發佈:2018-12-10
另一種視角定義SVM:hinge Loss +kennel trick
SVM 可以理解為就是hingle Loss和kernel 的組合
1. hinge Loss
還是讓我們回到二分類的問題,為了方便起見,我們y=1 看做是一類,y=-1 看做是另一類


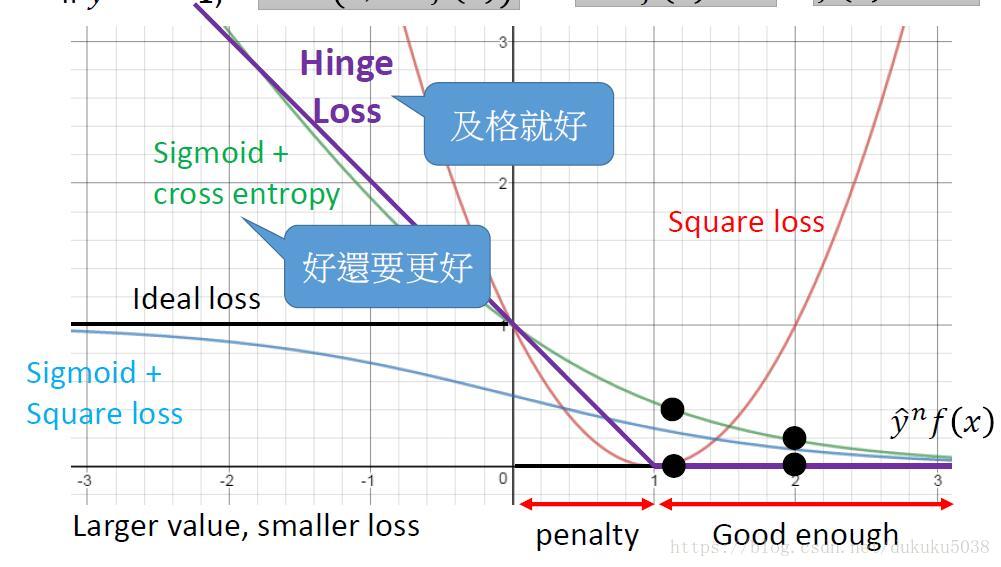
在這裡,我們引入hinge Loss,它的公式:
含義是:當分類是1,,需要最大化0與的值,, 比1越大越好;
當分類是1,,需要最大化0與的值,, 比-1越x小越好
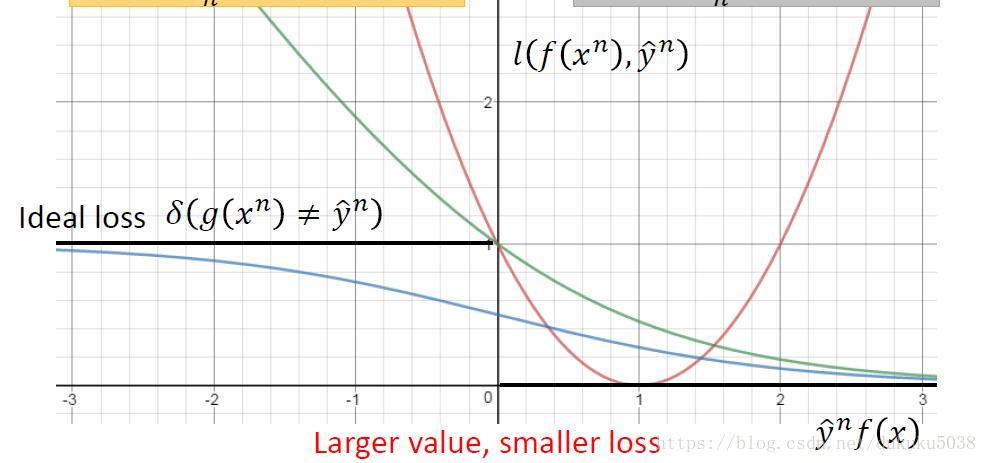
所以它的Loss影象為(紫色的線段):


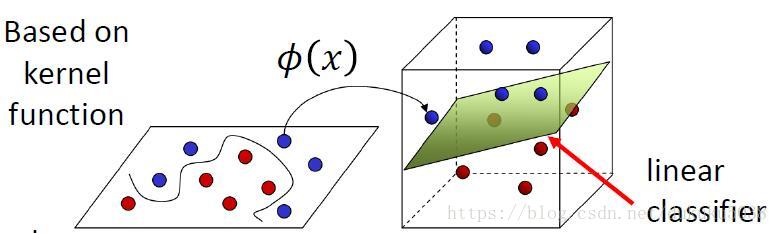
2. Kernel
通常,我們需要對我們的資料在高維空間進行相關對映。
我們通過拉格朗日乘子法,得到最優的w是 x的線性組合
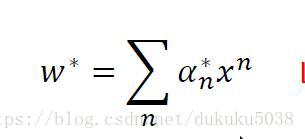
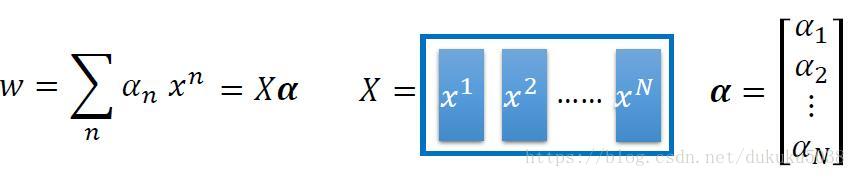
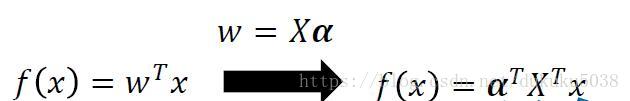
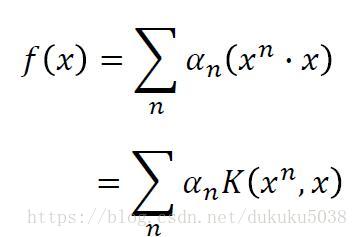

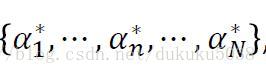
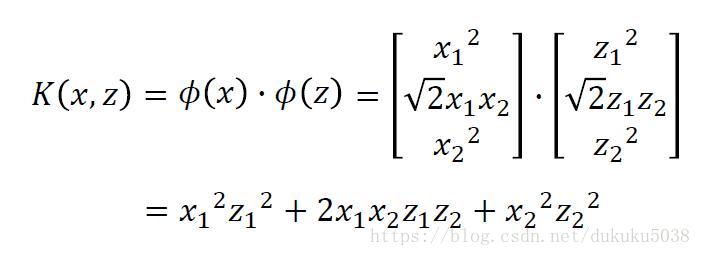
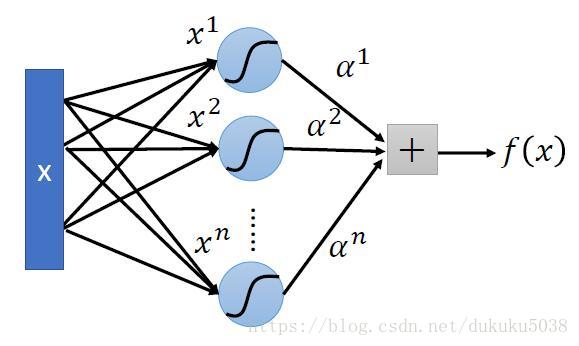
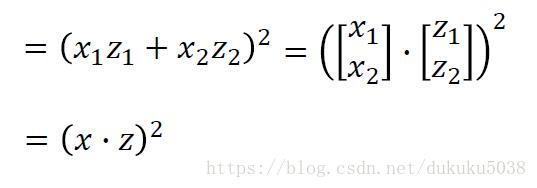 有很多kernel的例子:Sigmoid Kernel
有很多kernel的例子:Sigmoid Kernel
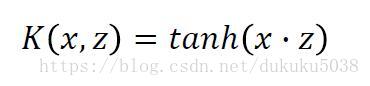
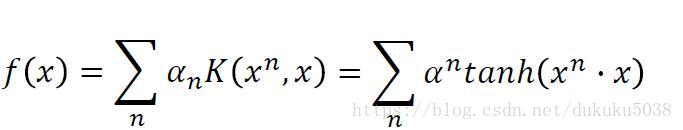 畫成圖: 是不是就是一個神經網路呢? 恍然所思,殊途同歸!
畫成圖: 是不是就是一個神經網路呢? 恍然所思,殊途同歸!