非旋轉式treap及可持久化
阿新 • • 發佈:2019-02-15
簡介:
Treap,一種表現優異的BST
優勢:
其較於AVL、紅黑樹實現簡單,淺顯易懂
較於Splay常數小,通常用於樹套BST表現遠遠優於Splay
或許有人想說SBT,SBT我沒有實現過,據說比較快
但是SBT、Splay以及旋轉版Treap等BST都不可以比較方便地實現‘可持久化操作’
介紹:
Treap=Tree+Heap Treap是一顆同時擁有二叉搜尋樹和堆性質的一顆二叉樹 Treap有兩個關鍵字,在這裡定義為: 1.key,滿足二叉搜尋樹性質,即中序遍歷按照key值有序 2.fix,滿足堆性質,即對於任何一顆以x為根的子樹,x的fix值為該子樹的最值,方便後文敘述,定義為最小值 為了滿足期望,fix值是一個隨機的權值,用來保證樹高期望為logn 剩下的key值則是用來維護我們想要維護的一個權值,此為一個二叉搜尋樹的基本要素
支援操作:
基本操作:
1.Build【構造Treap】【O(n)】
2.Merge【合併】【O(logn)】
3.Split【拆分】【O(logn)】
4.Newnode【新建節點】【O(1)】
可支援操作:
1.Insert【Newnode+Merge】【O(logn)】 2.Delete【Split+Split+Merge】【O(logn)】 3.Find_kth【Split+Split】【O(logn)】 4.Query【Split+Split】【O(logn)】 5.Cover【Split+Split+Merge】【O(logn)】 and more....
操作分析:
PS:如果沒有看懂可以在最後看看我的程式碼
1.Build
讓我們先來看看笛卡爾樹,笛卡爾樹同樣是一顆同時擁有二叉搜尋樹和堆性質的一顆二叉樹 ---> 笛卡爾樹【維基百科】 ---> 笛卡爾樹【百度百科】 笛卡爾樹構造是和Treap完全一樣的,如果key值是有序的,那麼笛卡爾樹的構造是線性的,所以我們只要把Treap當作一顆笛卡爾樹構造就可以了 簡要講講笛卡爾樹: 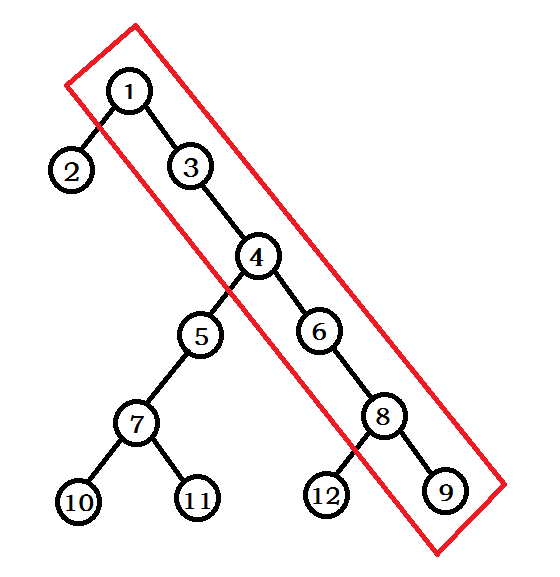
笛卡爾樹構造時用棧維護了整棵樹最右的一條鏈,每次在右下角處加入一個元素然後維護笛卡爾樹的性質
圖中,1、3、4、6、8、9為棧中元素,此時笛卡爾樹滿足所有性質,即在棧中元素fix值從1開始遞增,假設此時我們在9的右兒子添加了一個13,若13的fix值小於棧頂元素9的fix,那麼就開始退棧,停止退棧的條件有兩個,滿足任意一個即停止:
1.當前棧頂元素fix<13的fix【前面已經約定fix小的在上】
2.棧為空
若13的fix>3的fix並且<4的fix,那麼上圖會變為:
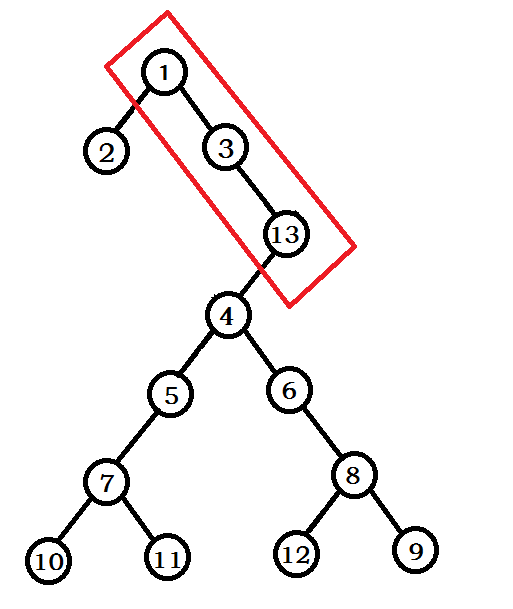
由於對於每個元素只會退棧一次,所以複雜度是O(n)
2.Merge
對於兩個相對有序的Treap【若中序遍歷為遞增,即TreapA的最右下角也就是最大值小於TreapB的最左下角也就是最小值】,那麼Merge的複雜度是O(logn)的;
對於兩個相對無序的Treap,那麼Merge只能啟發式合併了。
那麼Merge是如何操作的?
我們可以先來看看斜堆的Merge操作:
---> 斜堆【百度百科】
---> 可並堆【百度文庫】
非常好理解,斜堆的Merge是一個遞迴操作:
若當前要Merge(A,B),若A的val < B的val,交換A,B指標;
然後A的右子樹=Merge(A的右子樹,B);
最後交換一下A的左右子樹.
Treap的Merge也同理,只是需要注意滿足中序遍歷,因此不能交換左右子樹,需要自行特判,程式碼也很簡潔
3.Split
對於一個Treap,我們需要把它按照第K位拆分,那應該怎麼做呢?
就像在尋找第K位一樣走下去,一邊走一邊拆樹,每次返回的時候拼接就可以了
由於樹高是logn的,所以複雜度當然也是logn的
這樣Treap有了Split和Merge操作,我們可以做到提取區間,也因此可以區間覆蓋,也可以區間求和等等
除此之外因為沒有了旋轉操作,我們還可以進行可持久化,這個下文會講到
4.Newnode
這個就不說了
5.可支援操作
一切可支援操作都可以通過以上四個基本操作完成:
Build可以用來O(n)構樹還可以在替罪羊樹套Treap暴力重構的時候降低一個log的複雜度
Merge和Split可用提取區間,因此可以操作一系列區間操作
Newnode單獨拿出來很必要,這樣在可持久化的時候會很輕鬆
可持久化
可持久化是對資料結構的一種操作,即保留歷史資訊,使得在後面可以呼叫之前的歷史版本
對於可持久化,我們可以先來看看主席樹(可持久化線段樹)是怎麼可持久化的:
---> 可持久化線段樹【blog】
由於只有父親指向兒子的關係,所以我們可以線上段樹進入修改的時候把沿途所有節點都copy一遍
然後把需要修改的指向兒子的指標修改一遍就好了,因為每次都是在原途上覆蓋,不會修改前一次的資訊
由於每次只會copy一條路徑,而我們知道線段樹的樹高是log的,所以時空複雜度都是nlog(n)
我們來看看旋轉的Treap,現在應該知道為什麼不能可持久化了吧?
如果帶旋轉,那麼就會破環原有的父子關係,破環原有的路徑和樹形態,這是可持久化無法接受的
如果把Treap變為非旋轉的,那麼我們可以發現只要可以可持久化Merge和Split就可一完成可持久化
因為上文說到了‘一切可支援操作都可以通過以上四個基本操作完成’,而Build操作只用於建造無需理會,Newnode就是用來可持久化的工具
我們來觀察一下Merge和Split,我們會發現它們都是由上而下的操作!
因此我們完全可以參考線段樹的可持久化對它進行可持久化
每次需要修改一個節點,就Newnode出來繼續做就可以了
Code
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<ctime>
using namespace std;
#define maxn 2000005
#define rep(i,x,y) for(int i=x;i<=y;++i)
#define dep(i,x,y) for(int i=x;i>=y;--i)
struct Treap{
Treap *l,*r;
int fix,key,size;
Treap(int key_):fix(rand()),key(key_),l(NULL),r(NULL),size(1){}
inline void updata(){
size=1+(l?l->size:0)+(r?r->size:0);
}
}*root;
typedef pair<Treap*,Treap*> Droot;//用來Split返回兩個根
inline int Size(Treap *x){return x?x->size:0;}//這樣求size可以防止訪問空指標
Treap *Merge(Treap *A,Treap *B){//合併操作
if(!A)return B;
if(!B)return A;
if(A->fix<B->fix){
A->r=Merge(A->r,B);
A->updata();
return A;
}else{
B->l=Merge(A,B->l);
B->updata();
return B;
}
}
Droot Split(Treap *x,int k){//拆分操作
if(!x)return Droot(NULL,NULL);
Droot y;
if(Size(x->l)>=k){
y=Split(x->l,k);
x->l=y.second;
x->updata();
y.second=x;
}else{
y=Split(x->r,k-Size(x->l)-1);
x->r=y.first;
x->updata();
y.first=x;
}
return y;
}
Treap *Build(int *a){//建造操作
static Treap *stack[maxn],*x,*last;
int p=0;
rep(i,1,a[0]){
x=new Treap(a[i]);
last=NULL;
while(p && stack[p]->fix>x->fix){
stack[p]->updata();
last=stack[p];
stack[p--]=NULL;
}
if(p) stack[p]->r=x;
x->l=last;
stack[++p]=x;
}
while(p) stack[p--]->updata();
return stack[1];
}
int Findkth(int k){//查詢第K小
Droot x=Split(root,k-1);
Droot y=Split(x.second,1);
Treap *ans=y.first;
root=Merge(Merge(x.first,ans),y.second);
return ans->key;
}
int Getkth(Treap *x,int v){//詢問一個數是第幾大
if(!x)return 0;
return v<x->key?Getkth(x->l,v):Getkth(x->r,v)+Size(x->l)+1;
}
void Insert(int v){//插入操作
int k=Getkth(root,v);
Droot x=Split(root,k);
Treap *n=new Treap(v);
root=Merge(Merge(x.first,n),x.second);
}
void Delete(int k){//刪除操作
Droot x=Split(root,k-1);
Droot y=Split(x.second,1);
root=Merge(x.first,y.second);
}
int a[maxn],M,x,y;
int main(){
freopen("bst.in","r",stdin);
freopen("bst.out","w",stdout);
scanf("%d",a);
rep(i,1,a[0]) scanf("%d",a+i);
sort(a+1,a+1+a[0]);
root=Build(a);
scanf("%d",&M);
while(M--){
char ch=getchar();
while(ch!='Q' && ch!='A' && ch!='D') ch=getchar();
scanf("%d",&x);
if(ch=='Q') printf("%d\n",Findkth(x));
if(ch=='A') Insert(x);
if(ch=='D') Delete(x);
}
} 