最優化方法:四、一維搜尋法
阿新 • • 發佈:2019-02-15
主要參考書目:
- 最優化方法及其應用/郭科,陳聆,魏友華.-北京:高等教育出版社,2007.7(2013.7重印)
迭代的基本公式是
當我們確定了搜尋方向,我們要做的就是確定一個步長,使得,從而也就確定了,記為。尋找的過程即稱是一維搜尋。
對於一個確定的目標函式,一維搜尋等價於以下兩式:
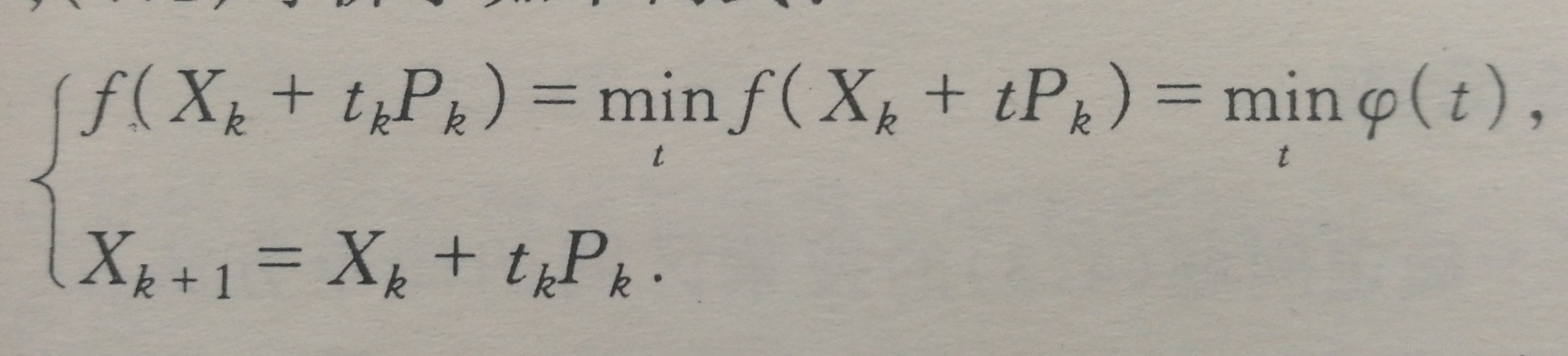
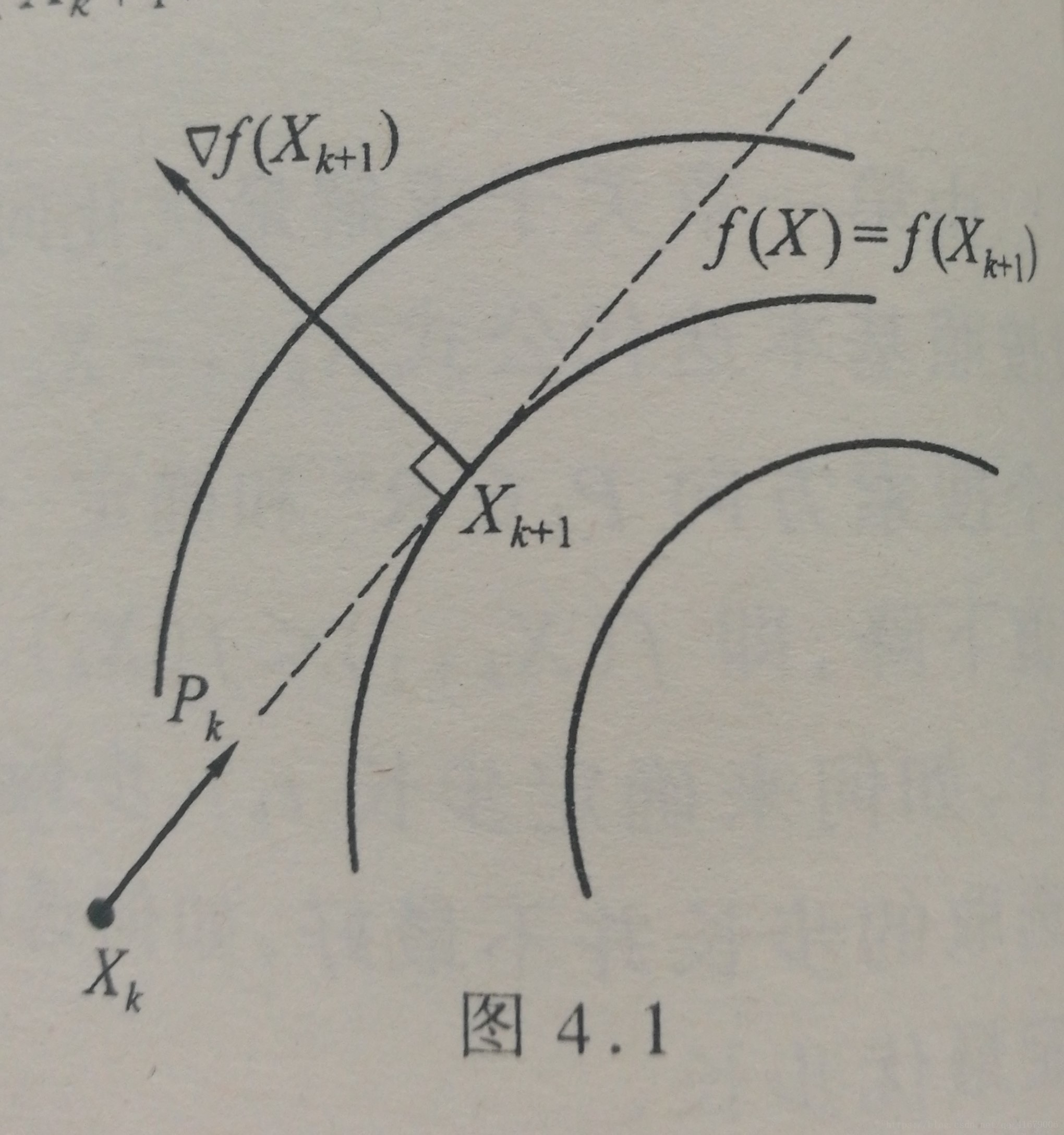
可以證明,在處滿足如下圖:
1、一些概念
- 搜尋區間
即是包含問題最優解的一個區間。 - 單谷區間與單谷函式
定義:
有性質:
根據此性質,我們可以將一個已知的單谷區間縮短為一個更小的單谷區間,從而無限接近於最優解。
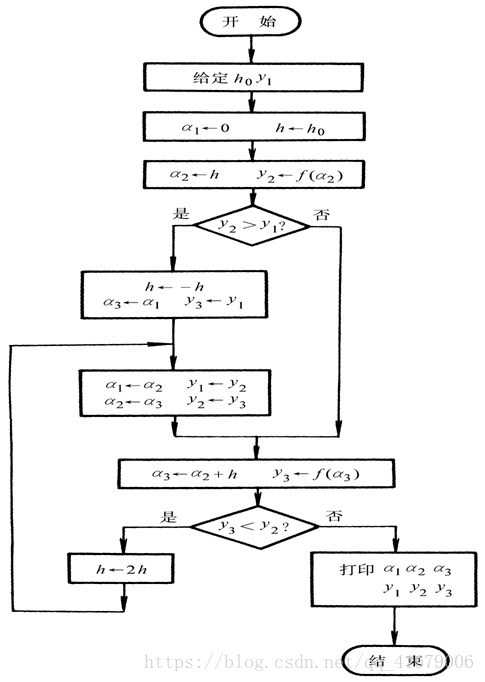
2、進退法(加步搜尋法)
該方法主要用於確定初始搜尋區間。
- 基本原理:
我們即是要尋找如圖c的情況。 - 計算步驟
該流程圖中初始點賦的值為0,實際上可以是任意值。 - matlab實現
function [a,b] = JinTui(f,xk0,d,th)
%進退法求搜尋區間
%輸入:
% f:目標函式的控制代碼
% xk0:初始值 2、對分法
- 基本思路
在一個單谷區間內,求函式的極小值即是求的點。此對分法即是求函式零點的對分法,不再贅述。 - 特點
此方法要求“單谷”,也要求原函式導數存在。
3、牛頓切線法
- 基本思路
與對分法類似,同樣是把求函式的極小值轉化為求的點。此時的牛頓切線法也就是求函式零點的牛頓切線法,亦不贅述。 - 特點
此方法同樣要求“單谷”,也要求原函式二階導數存在。
該方法若使用恰當收斂很快,但同時也容易出現不能收斂的問題。
4、黃金分割法
- 基本思路
利用單谷區間的性質,縮短區間,點選為區間的兩個黃金分割點。 - 特點
只要求“單谷”。
5、拋物線插值法
- 基本思路
通過用拋物線擬合目標函式的方法求取近似極小值。
不妨設單谷搜尋區間為,再任取,根據此三點確定一個拋物線,求出其最小值點,若精度不滿足要求,再利用單谷區間的性質縮短區間進一步迭代。 - 具體內容