1：高斯消元法演算法步驟

1:選擇主元；即選擇對角元素，保證其為所在列的最大，避免大數除以小數出現溢位，其實是避免其值為0；
2:當前主元不為最大值，交換兩行；
3:判斷主元是否為0，若是則不是唯一解;
4:逐行消元；
5:對角線元素歸一化；
6:回代消除對角線之上的元素。

2：演算法結果展示

百度知道上的一道題目，用來測試
圖中是原題給出的答案：

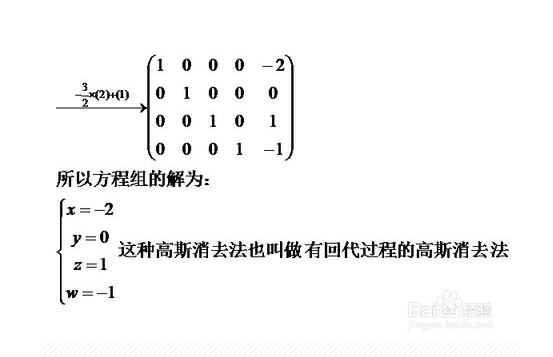
下圖是演算法給出的答案

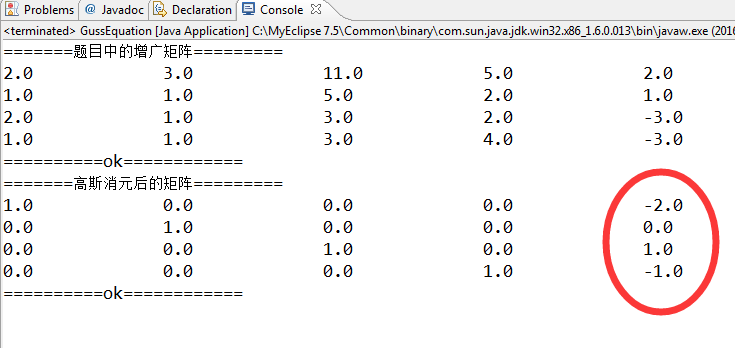
這樣看來結果還是很不錯的。

3：程式碼

這個是主方法，主要是使用一維陣列實現，對應的方法引數要給出方程增廣矩陣的每一行的個數。
內部方法將在後面給出，這個方法可以直接使用。

    /**
     * 
     * @param array 係數矩陣 增廣矩陣
     * @param colNum 列向量個數（從第0列開始）
     * @return boolean 是否得出結果
     */
    public  boolean Resolve(float[] array, int colNum){

        //行數
        int rows = array.length / colNum ;


        //逐行選擇主元              第 i 行 ，第i列  的元素（i，i）
        for (int i = 0
 
; i < rows; i++) {

            //按列選擇主元
            int pivotRow = SelectPivotalElement(array,colNum,i);

            //如果主元不是目前所在的i列，則交換
            if(pivotRow!=i){
                swapCol(array,pivotRow,i,colNum);
            }

            if(array[i*colNum+i]==0){
                System.out.println("不含有唯一解"
 
);
                return false ;
            }

            //消元得到上三角
            for (int j = 0; j < colNum; j++) {
                emissElement(array,j,colNum);
            }

        }

        //主元素歸一化
        for (int i = 0; i < rows; i++) {
            ElementBack(array,i,colNum);
        }

        //回代消元，從最後一行開始
        for (int i = rows-1; i > 0; i--) {
            backEmiss(array,i,colNum);
        }

        return true ;

    }

用於內部實現的各個方法

    /**
     * 回代消元
     * @param array
     * @param i 第i行之上的開始消除
     * @param colNum 矩陣每一行的個數
     */
    private static void backEmiss(float[] array, int i, int colNum) {

        for (int j = i; j >0; j--) {
            float fractor = array[(j-1)*colNum+i] ;
            array[(j-1)*colNum+i] = 0 ;
            array[j*colNum-1] = array[j*colNum-1] -  array[(i+1)*colNum-1]*fractor ;
        }

    }

    /**
     * 元素歸一化處理
     * @param array
     * @param i 第 i 行 歸一化處理
     * @param colNum 矩陣列數 ，每行元素個數
     */
    private static void ElementBack(float[] array, int i, int colNum) {

        //每行的長度
        int len = array.length / colNum ;

        float factor = array[i * colNum + i] ;
        for (int j = i * colNum + i; j < (i+1)*colNum; j++) {
            array[j] = array[j] / factor ;
        }

    }

    /**
     * 逐行消元
     * @param array
     * @param i 標示第 i 行的主元
     * @param colNum
     */
    private static void emissElement(float[] array, int i, int colNum) {

        //矩陣行數
        int len = array.length / colNum ;

        //第i+1行開始消元
        for (int j = (i+1); j <len; j++) {
         //int j = 1 ;
            //消元係數
            float index = array[j*colNum+i] / array[i * colNum + i] ;
            int ii = i * colNum + i ;
            for (int k = j*colNum + i; k < (j+1)*colNum  ; k++,ii++) {
                array[k] = array[k] - array[ii]*index ; 
            }

        }


    }

    /**
     * 交換兩行
     * @param array
     * @param dist 目標行
     * @param src  原來的行
     * @param colNum 行向量的長度
     */
    private static void swapCol(float[] array, int dist, int src,int colNum) {


        int distance = (dist - src)*colNum ;

        for (int j = src*colNum; j < (src+1)*colNum; j++) {
            float temp = array[j] ;
            array[j] = array[j+distance] ;
            array[j+distance] = temp ;

        }

    }

    /**
     * 
     * @param array
     * @param colNum
     * @param i  第i行的主元
     * @return 主元所在的列
     */
    private static int SelectPivotalElement(float[] array,int colNum,int i) {


        //返回的所選擇的主元所在列的索引
        int pivotColIndex = 0 ;

        //中間變數
        float max = 0 ;


        for (int j = i*colNum + i; j < array.length; j+=colNum) {
            if(Math.abs(max)<Math.abs(array[j])){
                max = array[j];
                pivotColIndex = j ;
            }
        }
        //返回主元所在的行
        return pivotColIndex/colNum;
    }