回顧

上文中我們討論了全函式和部分函式，以及計算的可終止性。
本文我們從數論函式開始，給原始遞迴函式集增加一種新的運算，得到了一個更大的集合。
然後根據遞迴函式，我們可以定義遞迴集和遞迴可列舉集，
為以後討論可計算性與可判定性打好基礎。

數論函式

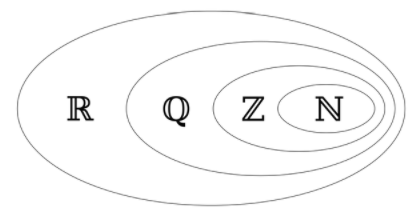
自然數集一般記為N={0,1,2,⋯}N={0,1,2,⋯}，那麼nn個自然數集的笛卡爾積記為NnNn，
於是，我們稱集合NnNn到NN的部分函式為nn元部分數論函式。
作為數論函式，2x2x是一個全函式，而x/2x/2，x−yx−y，x√x只是部分函式，
它們的計算結果，3/23/2，4−64−6，5√5都不在NN中，於是相應定義域中的點可視為沒有定義。

為什麼討論數論函式呢，其一是因為它是一個典型數學的問題，
另外一點，則是因為我們經常把其他數學問題轉換成數論問題，例如，哥德爾編碼。
本文中，使用數論函式，可以簡化我們的描述方式。

一個謂詞，指的是返回布林值的函式，
我們還可以將謂詞看做值域為{0,1}{0,1}的一個數論函式。
00代表True，11代表False。

極小化運算元

在前一篇中，我們從三個初始函數出發，
通過合成運算和原始遞迴運算，得到了原始遞迴函式集，
遞迴函式集是相對於這兩種運算封閉的。

然而，這樣定義的原始遞迴函式，並不能包括所有的數論函式，
一個典型的例子就是，阿克曼函式，

ackermann ::
 
 Int -> Int -> Int
ackermann 0 x = x+1
ackermann k 0 = ackermann (k-1) 1
ackermann k x = ackermann (k-1) $ ackermann k x-1

它並不是一個原始遞迴函式，（證略
因此原始遞迴函式集並不足以表示計算機程式中的所有函式。

為此，我們需要對原始遞迴函式集進行擴充，我們定義一個新的運算，稱為極小化運算，
設P(x1,⋯,xn,t)P(x1,⋯,xn,t)是一個謂詞，令
f(x1,⋯,xn)=minP(x1,⋯,xn,t)f(x1,⋯,xn)=min P(x1,⋯,xn,t)

f(x1,⋯,xn)f(x1,⋯,xn)的值，或者是使

相關推薦