前面我們講到棧和佇列的時候，這兩種資料結構都是按時間的先後順序來排列，如棧是按先進後出（FILO），後入先出的原則排列。而佇列是按先進先出（FIFO）的原則排序。但有時候按這種時間原則的資料結構不能滿足使用者的一些需求，例如CPU需要執行程式的優先級別，很多時候不能靠時間順序，有些程式重要性更高的時候，應該優先被呼叫，所以應該用一種按優先順序高低來排列的資料結構，資料結構中的每一個物件都有各自的優先順序，我們從這個結構序列中取出元素的原則是按優先順序的高低來取出，而不是進入佇列的先後順序。這裡就要用到一種資料結構：堆。如果我們要用二叉搜尋樹來實現堆這一結構，怎麼做？

這裡舉例用最大堆，最大堆的二叉搜尋樹結構是，從根結點開始，每一個結點的優先順序都比它的左右子樹高。這樣來實現的話，我們可以把二叉搜尋樹用一種平衡的，排好序的結構來儲存從而提高後面操作的效率，那就是用完全二叉樹。

堆最重要的特點就是結構有序性。用完全二叉樹的結構，有序性分兩種，一種是最大堆，也就是從根結點開始，任一結點的元素優先順序都比它的左右子樹高。第二種是最小堆，也就是從根結點開始，任一結點的元素優先順序都比它的左右子樹低。

那麼對於堆的操作，最基本的有建堆，插入和刪除三種。

最大堆的結構：

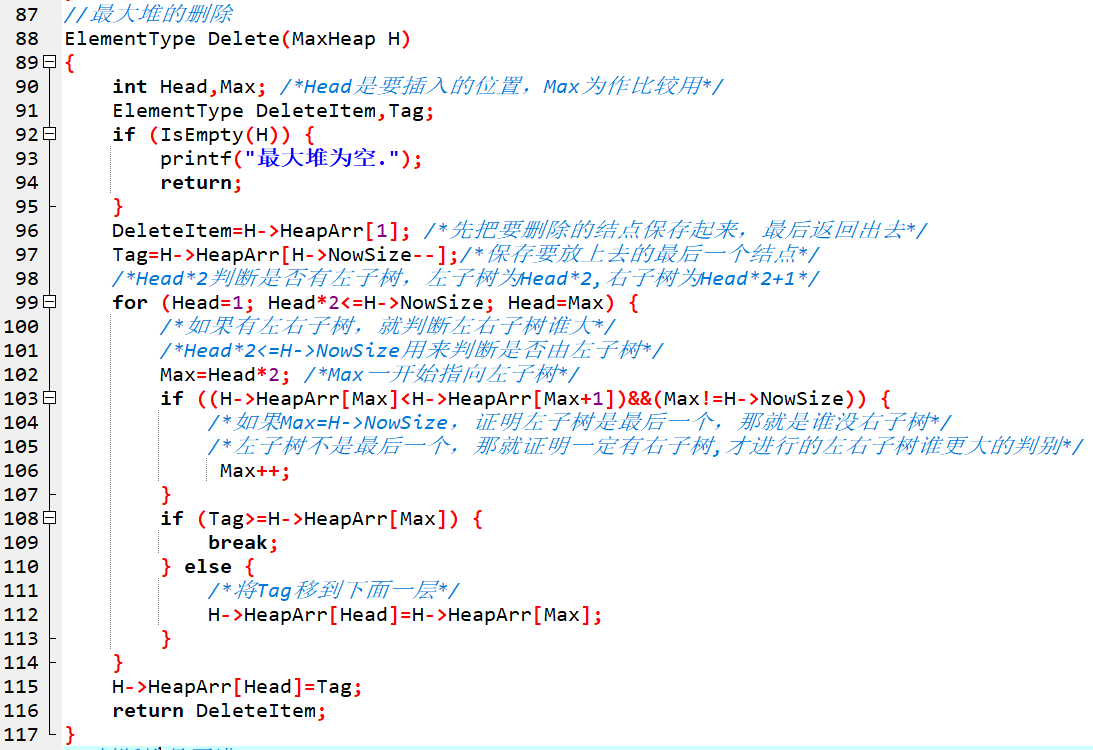
先說刪除，因為最大堆的建立方法和刪除是相似的

首先定義兩個下標變數Max和Head用來下面找插入點，然後一開始判斷堆空不空，空就直接結束了。刪除的方法就是刪除根結點後，在樹的最後一個元素替換上來根結點的位置，最後一個元素在H->HeapArr[NowSize]的位置。接下來程式的迴圈就是找出這個最後一個元素應該換到樹的哪一個位置上。首先讓

接著是插入。

按順序插入，所以每次要插入的元素都放在陣列的最後，就是i=++H->NowSize的地方。插入後，還要調整結點保持有序性，也就是保證每個結點都比其左右子樹大。所以插入後還要用個迴圈來做比較，插入後的結點（i為下標位置）和它的父結點i/2，比較，如果結點比它的父結點大，就要調整位置，把父結點的值賦給

最後是最大堆的建立，方法和刪除操作相似。

在按順序插入完所有元素後，從最後一個元素開始和其父結點作比較。定義一個X來儲存最後一個元素，然後和父結點比較，大的就往上移，最後調整出一個有序的堆。