Unity Shader:實現菲涅爾+色散效果以及相關原理解析
1,色散在光學中的原理
2,反射的原理以及環境對映的實現
3,折射的原理以及色散的實現
4,菲涅爾效果
5,將菲涅爾與色散效果增加到環境對映中
1,色散在光學中的原理
複色光
——現實生活中的許多光都是複色光,例如陽光。
光譜
——光學頻譜,簡稱光譜,是複色光通過色散系統(如光柵、稜鏡)進行分光後,依照光的波長(或頻率)的大小順次排列形成的圖案。
https://zh.wikipedia.org/wiki/%E5%85%89%E5%AD%B8%E9%A0%BB%E8%AD%9C
色散
——複色光通過介質產生折射時,由於各個通過複色光中各個光的波長不同而導致的折射率不同所產生各個光線依次分開。
2,反射的原理以及環境對映的實現
反射可以用來解釋你在鏡子或水面中看到的景象。將你看向鏡面的視角抽象為一組向量,當這組向量接觸到鏡面後會生成一組反射向量,而這組反射向量再次接觸到的點的集合既是你在鏡面中所見的景象。
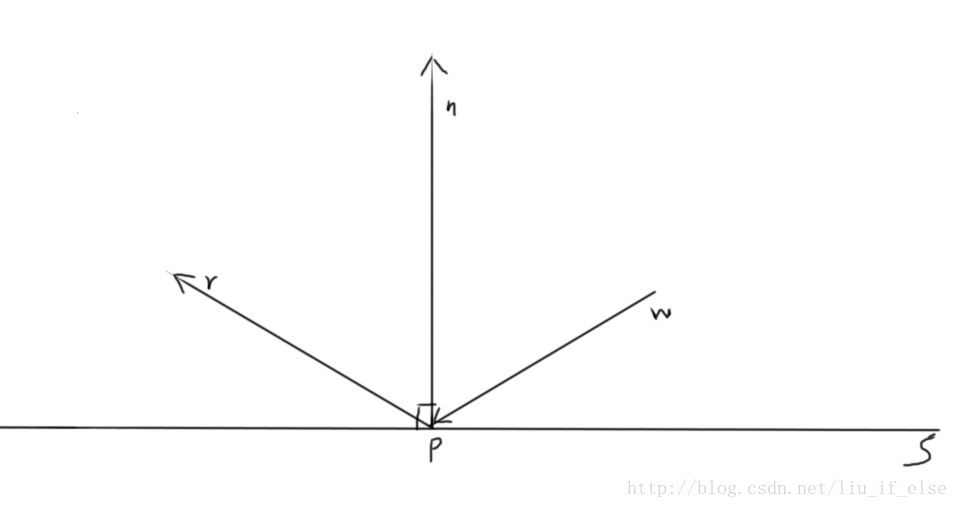
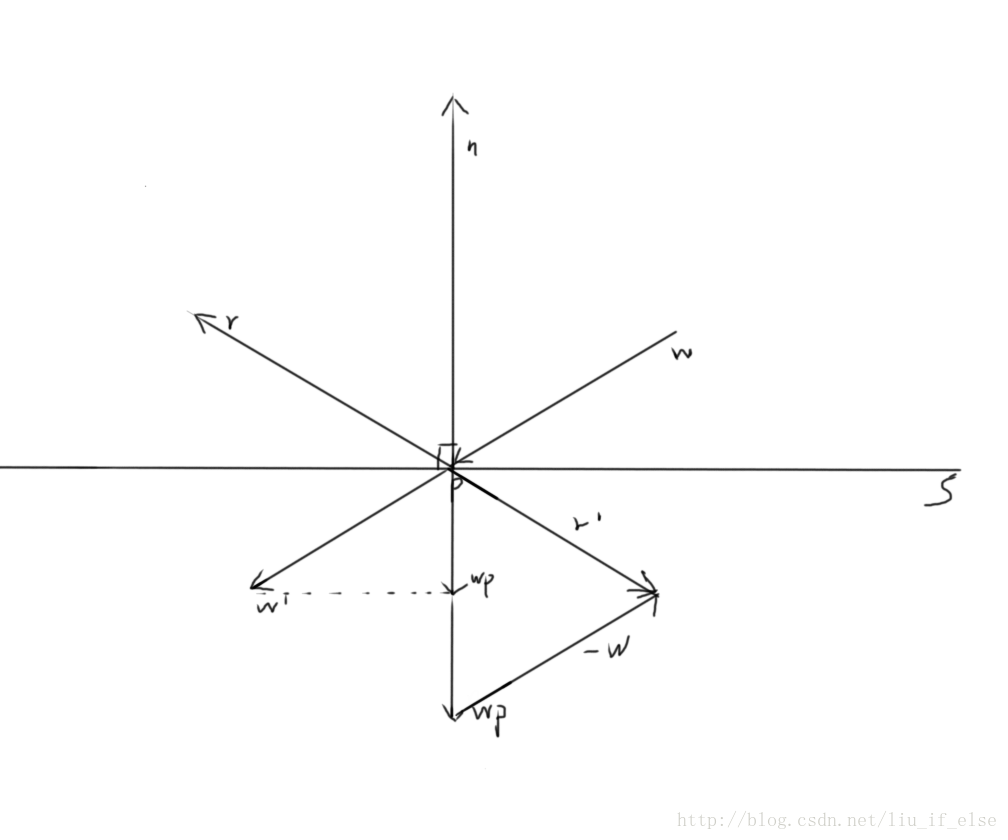
二維中看起來比較簡單,w為入射向量,r為反射向量,S為反射介質,P為反射點,n垂直於S。只要做到w與s的夾角與r與s的夾角相等,既做到了反射。
但在三維中,是通過一系列向量運算來尋找反射向量的。
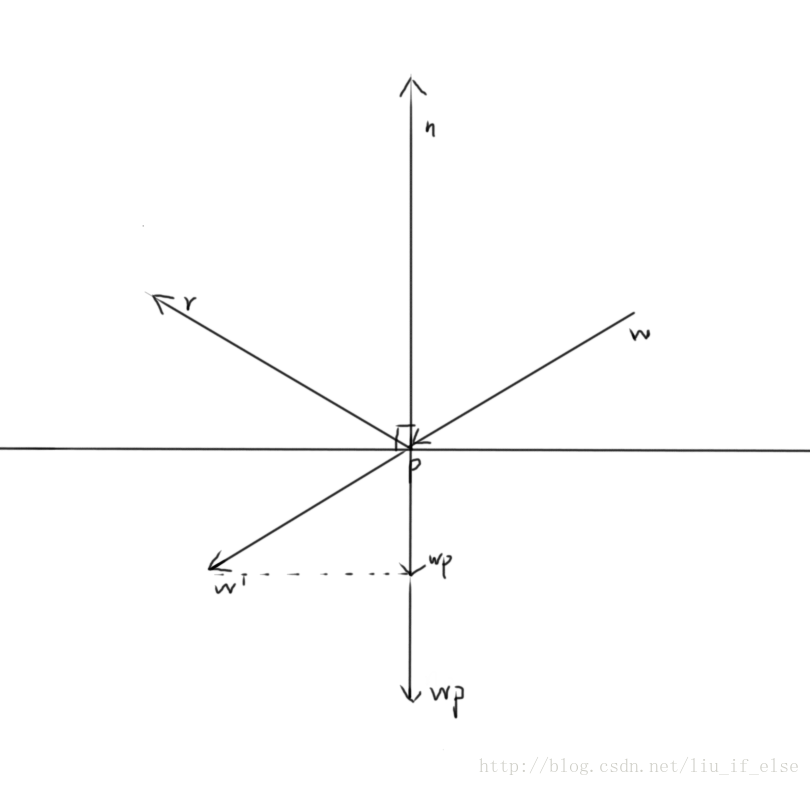
首先計算w的projection,並移到下方。視覺上理解既是將w移到w’處,n向下延伸,從w’做一條垂直於n的虛線,n的延伸與虛線的交點既是向量wp的終點,wp=dot(w,n/|n|),然後再做一條wp。在wp*2的終點畫一條’-w’,根據向量的加法法則,r’=wp*2-w, -r’=r既是w的反射向量。
用數學公式表達則是:
wp=dot(w,n/|n|) , wp is the projection of w on n.
r’=wp*2-w
r=-r’ ,w的反射向量
而在Shader中,以上這些都被簡化成了一個方法:
float r=reflect(w,n);環境對映既是利用反射對天空盒進行立方體取樣,模擬現實中的映象。
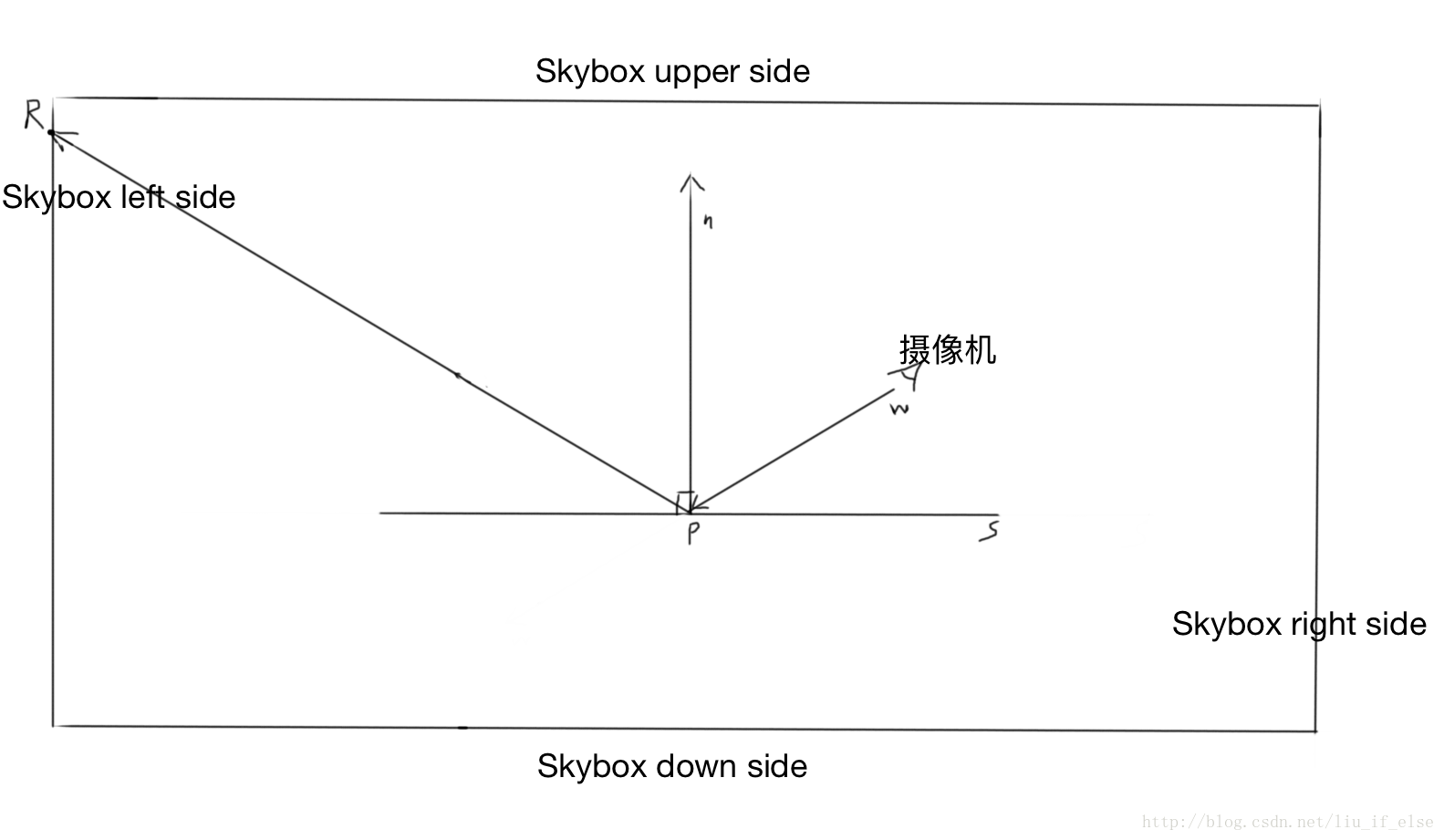
攝像機在鏡面S上所見的景象為Skybox左邊的點R。
以下程式碼為Unity官網的環境對映示例Shader。將插值與計算部分移到了片段著色器中,以優化顯示效果。
Shader "Unlit/SkyReflection" 效果:

這裡進一步解釋一下,當利用反射進行環境對映時,有弧度的物體的效果要明顯優於平面物體,因為有弧度的平面生成的反射向量角度更廣,在進行立方體取樣時模擬出的距離感更加真實。而由於天空盒與場景中的物體距離是有限的(而且其實並不是很遠), 平面物體生成的反射向量大部分都反射到了天空盒的一側的小部分割槽域,效果很失真,實際是由於這種反射”揭穿”了天空盒虛擬出的的無限遠效果。

上圖中立方體反射出星球的一小塊區域。
3,折射的原理以及色散的實現
折射可以解釋透過玻璃所看到的扭曲的景象。
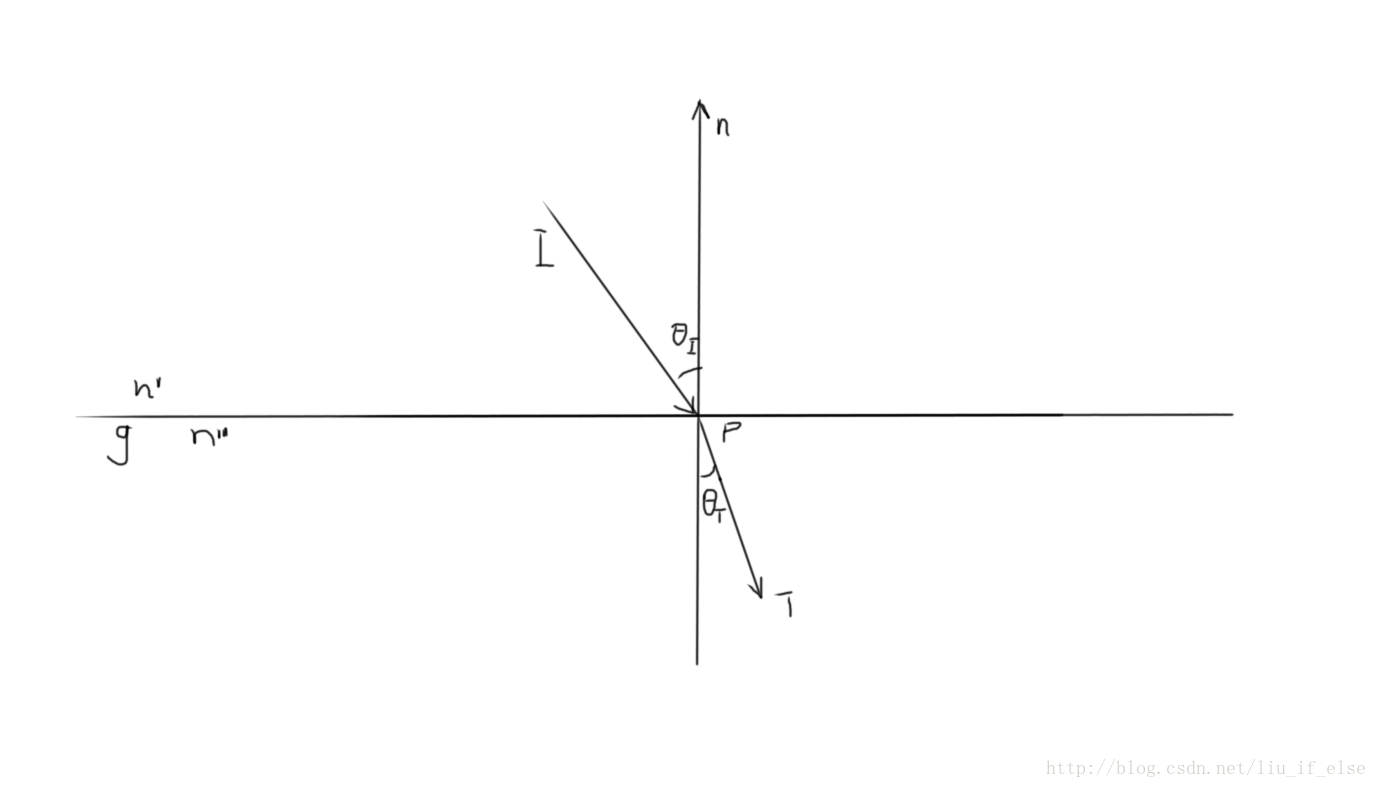
假設g為玻璃,空氣的折射率為n’,玻璃的折射率為n”
當入射向量接觸到介質g後,根據折射率n’與n”的差別,它的前行方向將會發生變化。
這種變化可用斯涅耳定律來進行計算:
snell’s law:
在Shader中,折射的計算也被簡化成了一個方法:
T=refract(I,n,etaRatio);其中etaRatio=n’/n”。
各種介質的etaRatio一覽:
————————————————
真空:1.0
水:1.3333
玻璃:1.5
鑽石:2.417
水晶: 1.544-1.553
————————————————
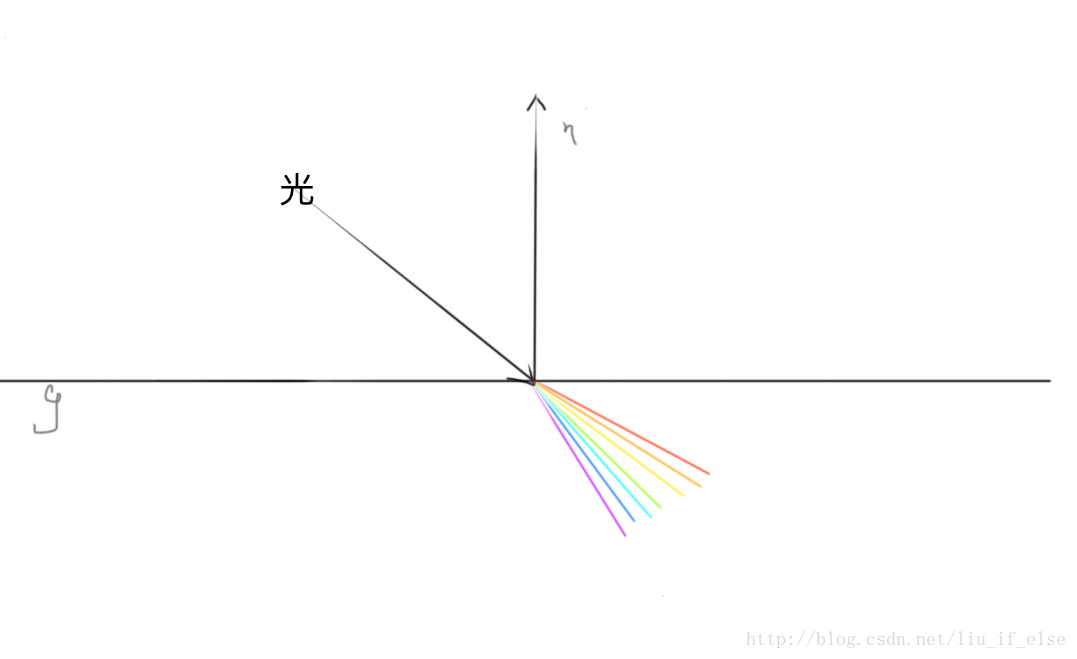
色散的實現:
最上面解釋過:複色光通過介質產生折射時,由於各個通過複色光中各個光的波長不同而導致的折射率不同所產生各個光線依次分開。
所以首先看下複色光中各個光的波長:
——————————
紅:620-750nm
橙:590nm
黃:570nm
綠:495nm
青:450nm
藍:420nm
紫:380nm
——————————
而由於折射率是取決於波長的,所以折射出的各個顏色的光的順序是一致的。
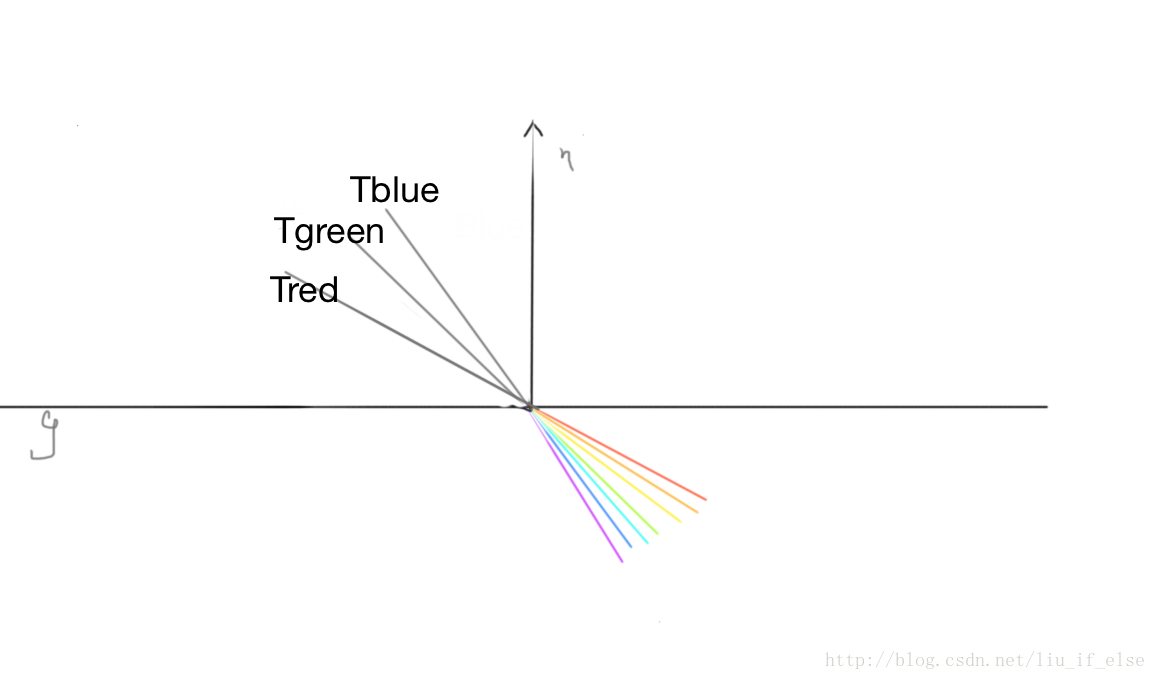
程式碼,這裡只用紅綠藍做示例:
先將折射率計算好,存在etaRatio的x,y,z中。
float3 Tred=refract(normalize(-worldViewDir),i.normal,etaRatio.x);
float3 Tgreen=refract(normalize(-worldViewDir),i.normal,etaRatio.y);
float3 Tblue=refract(normalize(-worldViewDir),i.normal,etaRatio.z);算出折射後的向量,分別進行立方體取樣,並只取相應的顏色。
float4 refractedColor;
refractedColor.r=DecodeHDR (UNITY_SAMPLE_TEXCUBE(unity_SpecCube0, Tred),unity_SpecCube0_HDR).r;
refractedColor.g=DecodeHDR (UNITY_SAMPLE_TEXCUBE(unity_SpecCube0, Tgreen),unity_SpecCube0_HDR).g;
refractedColor.b=DecodeHDR (UNITY_SAMPLE_TEXCUBE(unity_SpecCube0, Tblue),unity_SpecCube0_HDR).b;refractedColor既是在環境對映中模擬出的介質後方景象產生色散的效果。
實際是在環境對映的過程中偏移取樣角度反向的模擬出色散。Tblue,Tgreen,Tred既是上面反射取樣中的r,而入射角實際是在g的下方。
4,菲涅爾效果
這個沒能力具體的好好解釋了。總之有一個公式在shader裡可以使用,返回值將用於最終的反射顏色與折射顏色的lerp混合中。
公式中的fresnelBias,fresnelScale與fresnelPower的賦值將會影響最終效果,如何賦值的原理沒找到。我在下面的例子中賦值的power=4,scale=0.1,bias=-0.2。試驗中發現將返回值的可能範圍儘量精確至0-1效果最佳。
float reflectionfactor=min(1.0f,max(0,fresnelBias+fresnelScale*pow(1.0f+dot(normalize(-worldViewDir),i.normal),fresnelPower)));5,將菲涅爾與色散效果增加到環境對映中
綜合以上寫一個Shader:
Shader "Unlit/Dispersion"
{
Properties {
fresnelPower("fresnelPower",float)=0
fresnelScale("fresnelScale",float)=0
fresnelBias("fresnelBias",float)=0
_r("r",float)=0
_g("g",float)=0
_b("b",float)=0
}
SubShader
{
Pass
{
CGPROGRAM
#pragma vertex vert
#pragma fragment frag
#include "UnityCG.cginc"
struct v2f {
float3 normal:NORMAL;
float3 worldRefra : TEXCOORD0;
float4 pos : SV_POSITION;
float4 objectPOS:float;
};
//在外部可改為power=4,scale=0.1,bias=-0.2
float fresnelPower=1.0f;
float fresnelScale=1.0f;
float fresnelBias=0.3f;
//紅,綠,藍的折射率,從外部賦值,方便調整
float3 etaRatio;// =float3(0.83f,0.67f,0.55f); //1/1.3 1/1.5 1/1.8
float _r;
float _g;
float _b;
v2f vert (float4 vertex : POSITION, float3 normal : NORMAL)
{
v2f o;
o.pos = UnityObjectToClipPos(vertex);
o.normal=normal;
o.objectPOS=vertex;
return o;
}
//為了達到最佳效果,將所有計算都寫在了片段著色器內。
fixed4 frag (v2f i) : SV_Target
{
etaRatio=float3(_r,_g,_b);
i.normal = UnityObjectToWorldNormal(i.normal);
float3 worldPos = mul(unity_ObjectToWorld, i.objectPOS).xyz;
float3 worldViewDir = UnityWorldSpaceViewDir(worldPos);
//反射向量
float R=reflect(-worldViewDir,i.normal);
i.normal=normalize(i.normal);
//計算用來模擬色散的折射向量
float3 Tred=refract(normalize(-worldViewDir),i.normal,etaRatio.x);
float3 Tgreen=refract(normalize(-worldViewDir),i.normal,etaRatio.y);
float3 Tblue=refract(normalize(-worldViewDir),i.normal,etaRatio.z);
//菲涅爾factor,用來混合反射與折射顏色。
float reflectionfactor=min(1.0f,max(0,fresnelBias+fresnelScale*pow(1.0f+dot(normalize(-worldViewDir),i.normal),fresnelPower)));
//如果利用color存此變數,可以省去min與max。
// color reflectionfactor=fresnelBias+fresnelScale*pow(1.0f+dot(normalize(-worldViewDir),i.normal),fresnelPower);
half4 skyData = UNITY_SAMPLE_TEXCUBE(unity_SpecCube0, R);
//反射顏色
float4 reflectedColor=half4(DecodeHDR (skyData, unity_SpecCube0_HDR),1.0f);
float4 refractedColor;
//折射顏色
refractedColor.r=DecodeHDR (UNITY_SAMPLE_TEXCUBE(unity_SpecCube0, Tred),unity_SpecCube0_HDR).r;
refractedColor.g=DecodeHDR (UNITY_SAMPLE_TEXCUBE(unity_SpecCube0, Tgreen),unity_SpecCube0_HDR).g;
refractedColor.b=DecodeHDR (UNITY_SAMPLE_TEXCUBE(unity_SpecCube0, Tblue),unity_SpecCube0_HDR).b;
refractedColor.a=1.0f;
fixed4 c=0;
//混合
c=lerp(refractedColor,reflectedColor,reflectionfactor.x);
return c;
}
ENDCG
}
}
}效果:



上圖中一個玻璃球使用普通折射Shader,一個使用菲涅爾色散Shader。

加在一個人形模型上。
利用此Shader表現的晶體材質更加真實。