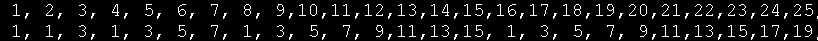使用環形連結串列實現約瑟夫環
阿新 • • 發佈:2019-02-17
連結串列實現Josephus約瑟夫環問題如下,輸出每輪殺掉的人的編號,並且輸出最後剩下的一名幸運者。
標頭檔案如下
#ifndef JOSEPHLIST_H #define JOSEPHLIST_H #include <stdio.h> typedef struct node *link; struct node{ int item; link next; }; link make_node(int item); void free_node(link p); void make_joseph_circle(int m); int joseph_number(int m, int n); void insert(link p); void delete_node(link p); void traverse(void (*visit)(link)); void destroy(void); #endif
實現如下
#include <stdlib.h> #include "josephlist.h" static link head = NULL; static link tail = NULL; link make_node(int item) { link p = new node; p->item=item; p->next=NULL; return p; } void free_node(link p) { if(p!=NULL) free(p); } void insert(link p) { if(head == NULL && tail ==NULL){ head = p; tail = p; p->next=head; }else{ tail->next = p; tail = p; tail->next = head; } } void delete_node(link p) { link pre; if(head==tail&&head==p) { head = NULL; tail = NULL; return; }else if(head==tail&&head!=p) { printf("impossible\n"); return; }else if(p==head){ head = head->next; tail ->next = head; // IMPORTANT O(∩_∩)O return; } for(pre=head;pre;pre=pre->next) { if(pre->next == p) { pre->next = p->next; if(p==tail) tail=pre; return; } } } void traverse(void (*visit)(link)) { link p; for(p=head;p!=tail;p=p->next) visit(p); visit(tail); } void destroy(void) { link p= head; link q= head; while(p!=tail) { q = p; p = p->next; free_node(q); } if(tail!=NULL) free_node(tail); head = NULL; tail = NULL; return; } void make_joseph_circle(int m) { if(head!=NULL) destroy(); for(int i=1;i<=m;i++){ link p = make_node(i); insert(p); } return; } int joseph_number(int m, int n) { make_joseph_circle(m); link p=head; link temp_next=p; int count=1; while(count<m) { for(int i=0;i<n-1;i++) { p = p->next; } printf("%d\t%d\n",count,p->item); temp_next = p->next; delete_node(p); free_node(p); p = temp_next; count++; } printf("LUCKY Joseph:%d\n\n",p->item); int result = p->item; if(p!=NULL) free_node(p); head=NULL; tail=NULL; return result; }
main函式如下
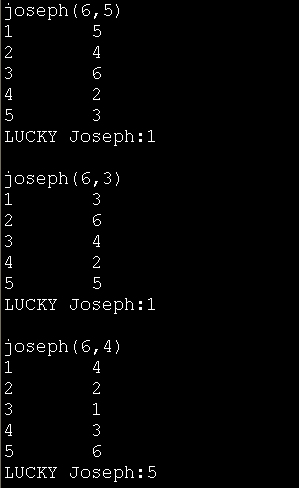
#include <stdio.h> #include "josephlist.h" void print_item(link p) { printf("%d\n",p->item); } int main() { printf("joseph(6,5)\n"); joseph_number(6,5); printf("joseph(6,3)\n"); joseph_number(6,3); printf("joseph(6,4)\n"); joseph_number(6,4); return 0; }
執行結果如下:
現在來探索一下每次得到的約瑟夫數的規律,從最簡單的開始。假設每次報數的時候,都1,2,1,2這樣的報數,報數為2的在此輪出列。那麼,總人數變化時,約瑟夫數如何變化呢?為了簡單,現在假設人數從1增長到25,每次報數為2時的變化情況:
把main函式改為如下:
#include <stdio.h>
#include "josephlist.h"
void print_item(link p)
{
printf("%d\n",p->item);
}
int main()
{
int total=25;
int result_people[26];
for (int i=1;i<=total;i++) {
result_people[i]=joseph_number(i,2);
}
for(int i=1;i<=total;i++)
{
printf("%d\t",i);
}
printf("\n");
for(int i=1;i<=total;i++)
{
printf("%d\t",result_people[i]);
}
printf("\n");
return 0;
}
約瑟夫數的結果構成了一個這樣的數列
1,
1,3
1,3,5,7
1,3,5,7,9,11,13,15,
...那麼,當每次報數為2時,如何從數學上推導約瑟夫數隨著總人數變化的遞推公式呢?又如何把報數從2推廣到N呢?還沒想出來。。。