設有n=2^k個運動員要進行網球迴圈賽，現要設計一個滿足以下要求的比賽日程表：
(1)每個選手必須與其他n-1個選手各賽一次；
(2)每個選手一天只能賽一次；
(3)迴圈賽一共進行n-1天。
按此要求在表中第i行和第j列處填入第i個選手在第j天所遇到的選手。
按分治策略，將所有的選手分為兩半，n個選手的比賽日程表就可以通過為n/2個選手設計的比賽日程表來決定。遞迴地用對選手進行分割，直到只剩下2個選手時，比賽日程表的制定就變得很簡單。這時只要讓這2個選手進行比賽就可以了。

演算法如下：

public class test2_11 {
    /**
     * 演算法table將迴圈賽日程表賦值到陣列a中
     * @param
 
 k 有n = 2^k個運動員
     * @param a 存放迴圈賽日程表，且賦值從下標1開始，下標0是空值。
     */
    public static void table(int k,int[][] a){
        int n=1;
        for(int i=1;i<=k;i++) n *= 2;
        for(int i=1;i<=n;i++) a[i][1] = i;
        int m = 1;    //控制陣列的下標，也預示分治到某一模組時該模組的間距
        for(int s=1;s<=k;s++){
            n /= 2
 
;   //若原n=8,則第一次劃分n/2=4組，第二次2組，第三次1組。
            for(int t=1;t<=n;t++)   //t表示每次劃分的組數，依次遞減
                for(int i=m+1;i<=2*m;i++)  //i∈[m+1,2*m]
                    for(int j=m+1;j<=2*m;j++){  //j∈[m+1,2*m]
                    //第一次謄抄對角線單位元素是一個，第二次是4個，第三次是8個，以此類推
                    //故第一次m=1時i,j∈[2,2],第二次m=2時i,j∈[3,4],第三次m=4時i,j∈[5,8]
 

                        a[i+(t-1)*2*m][j] = a[i+(t-1)*2*m-m][j-m];  
                        //根據劃分組數不同，組與組間距為(t-1)*2*m個元素
                        a[i+(t-1)*2*m-m][j] = a[i+(t-1)*2*m][j-m];
                    }
            m *= 2;
        }
    }
    public static void main(String[] args) {
        int n = 8;  //設有8個運動員
        int k = 3;  
        int[][] a = new int[n+1][n+1]; //0行和0列為空，從下標1開始賦值
        table(k,a);
        for(int i=1;i<=n;i++){
            for(int j=1;j<=n;j++)
                System.out.print(a[i][j]+" ");
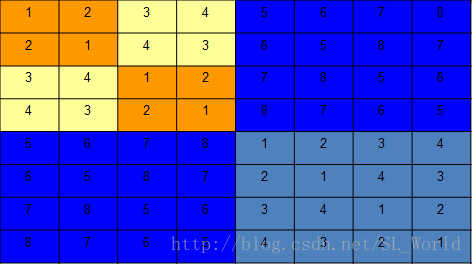
            System.out.println();
        }
    }
}

執行結果如下：

1 2 3 4 5 6 7 8 
2 1 4 3 6 5 8 7 
3 4 1 2 7 8 5 6 
4 3 2 1 8 7 6 5 
5 6 7 8 1 2 3 4 
6 5 8 7 2 1 4 3 
7 8 5 6 3 4 1 2 
8 7 6 5 4 3 2 1 

迴圈賽日程表打印出來了，可是計算機是按照怎樣的次序列印的呢？如下圖，第一列都是0因為謄抄是從第二列開始，次序從小到大表示先後列印次序。

0 2 10 12 26 28 30 32 
0 1 14 16 34 36 38 40 
0 4  9 11 42 44 46 48 
0 3 13 15 50 52 54 56 
0 6 18 20 25 27 29 31 
0 5 22 24 33 35 37 39 
0 8 17 19 41 43 45 47 
0 7 21 23 49 51 53 55

補充：此演算法是以固定列按行劃分組，如果想固定行按列劃分組，只需將第10行改為a[1][i]=i;以及第19行和21行演算法改為：

a[i][j+(t-1)*2*m] = a[i-m][j+(t-1)*2*m-m];  
a[i][j+(t-1)*2*m-m] = a[i-m][j+(t-1)*2*m];