1.前言

如果一直以來你只把GBM當作黑匣子，只知呼叫卻不明就裡，是時候來開啟這個黑匣子一探究竟了！

這篇文章是受Owen Zhang (DataRobot的首席產品官，在Kaggle比賽中位列第三)在NYC Data Science Academy裡提到的方法啟發而成。他當時的演講大約有2小時，我在這裡取其精華，總結一下主要內容。

不像bagging演算法只能改善模型高方差（high variance）情況，Boosting演算法對同時控制偏差（bias）和方差都有非常好的效果，而且更加高效。如果你需要同時處理模型中的方差和偏差，認真理解這篇文章一定會對你大有幫助，因為我不僅會用Python闡明GBM演算法，更重要的是會介紹如何對GBM調參，而恰當的引數往往能令結果大不相同。

特別鳴謝： 非常感謝Sudalai Rajkumar對我的大力幫助，他在AV Rank中位列第二。如果沒有他的指導就不會有這篇文章了。

2.目錄

1. Boosing是怎麼工作的？
2. 理解GBM模型中的引數
3. 學會調參（附詳例）

3.Boosting是如何工作的？

Boosting可以將一系列弱學習因子（weak learners）相結合來提升總體模型的預測準確度。在任意時間t，根據t-1時刻得到的結果我們給當前結果賦予一個權重。之前正確預測的結果獲得較小權重，錯誤分類的結果得到較大權重。迴歸問題的處理方法也是相似的。

讓我們用影象幫助理解：

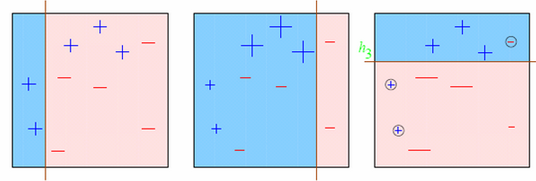
1. 圖一： 第一個弱學習因子的預測結果（從左至右）
   
   • 一開始所有的點具有相同的權重（以點的尺寸表示）。
   • 分類線正確地分類了兩個正極和五個負極的點。
2. 圖二： 第二個弱學習因子的預測結果
   
   • 在圖一中被正確預測的點有較小的權重（尺寸較小），而被預測錯誤的點則有較大的權重。
   • 這時候模型就會更加註重具有大權重的點的預測結果，即上一輪分類錯誤的點，現在這些點被正確歸類了，但其他點中的一些點卻歸類錯誤。

對圖3的輸出結果的理解也是類似的。這個演算法一直如此持續進行直到所有的學習模型根據它們的預測結果都被賦予了一個權重，這樣我們就得到了一個總體上更為準確的預測模型。

現在你是否對Boosting更感興趣了？不妨看看下面這些文章（主要討論GBM）：

4.GBM引數

總的來說GBM的引數可以被歸為三類：

1. 樹引數：調節模型中每個決定樹的性質
2. Boosting引數：調節模型中boosting的操作
3. 其他模型引數：調節模型總體的各項運作

從樹引數開始，首先一個決定樹的大致結構是這樣的：

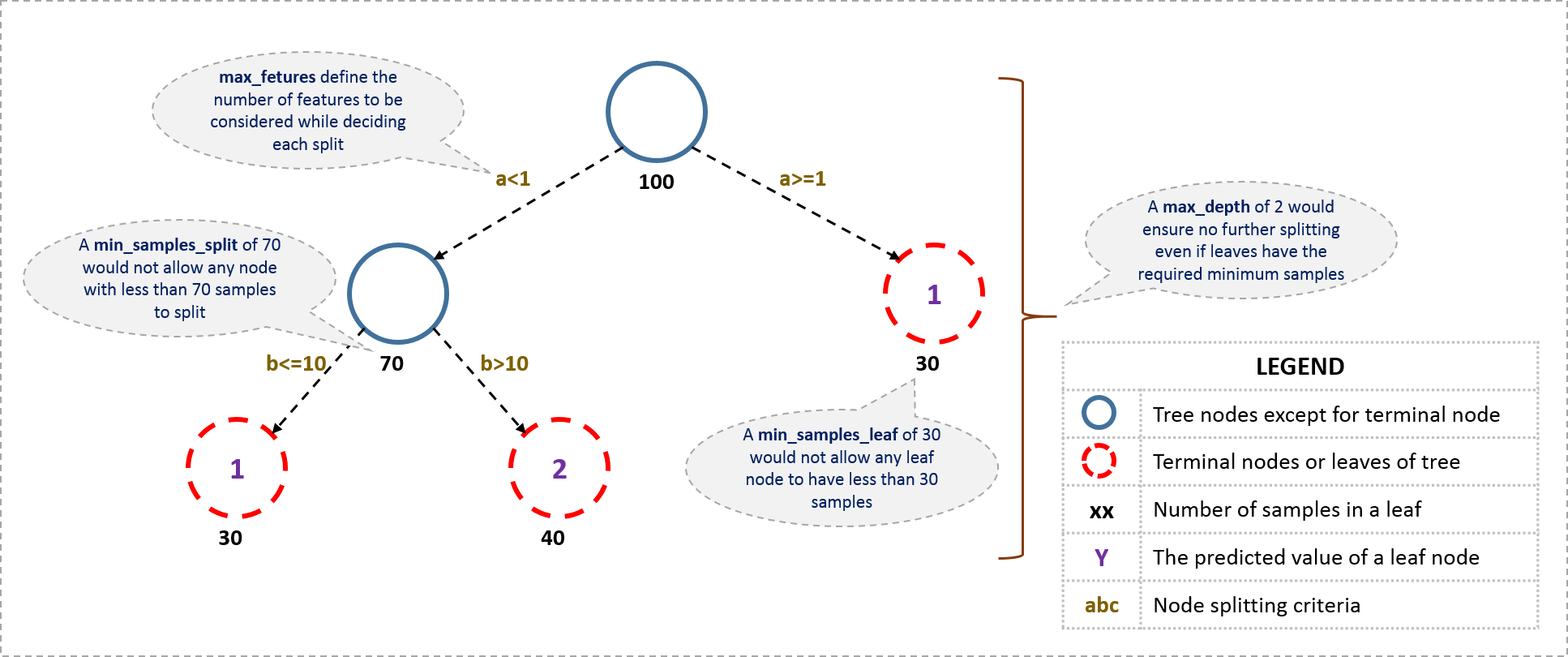
現在我們看一看定義一個決定樹所需要的引數。注意我在這裡用的都是python裡scikit-learn裡面的術語，和其他軟體比如R裡用到的可能不同，但原理都是相同的。

1. min_ samples_split
   
   • 定義了樹中一個節點所需要用來分裂的最少樣本數。
   • 可以避免過度擬合(over-fitting)。如果用於分類的樣本數太小，模型可能只適用於用來訓練的樣本的分類，而用較多的樣本數則可以避免這個問題。
   • 但是如果設定的值過大，就可能出現欠擬合現象(under-fitting)。因此我們可以用CV值（離散係數）考量調節效果。
2. min_ samples_leaf
   
   • 定義了樹中終點節點所需要的最少的樣本數。
   • 同樣，它也可以用來防止過度擬合。
   • 在不均等分類問題中(imbalanced class problems)，一般這個引數需要被設定為較小的值，因為大部分少數類別（minority class）含有的樣本都比較小。
3. min_ weight_ fraction_leaf
   
   • 和上面min_ samples_ leaf很像，不同的是這裡需要的是一個比例而不是絕對數值：終點節點所需的樣本數佔總樣本數的比值。
   • #2和#3只需要定義一個就行了
4. max_ depth
   
   • 定義了樹的最大深度。
   • 它也可以控制過度擬合，因為分類樹越深就越可能過度擬合。
   • 當然也應該用CV值檢驗。
5. max_ leaf_ nodes
   
   • 定義了決定樹裡最多能有多少個終點節點。
   • 這個屬性有可能在上面max_ depth裡就被定義了。比如深度為n的二叉樹就有最多2^n個終點節點。
   • 如果我們定義了max_ leaf_ nodes，GBM就會忽略前面的max_depth。
6. max_ features
   
   • 決定了用於分類的特徵數，是人為隨機定義的。
   • 根據經驗一般選擇總特徵數的平方根就可以工作得很好了，但還是應該用不同的值嘗試，最多可以嘗試總特徵數的30%-40%.
   • 過多的分類特徵可能也會導致過度擬合。

在繼續介紹其他引數前，我們先看一個簡單的GBM二分類虛擬碼：

1. 初始分類目標的引數值
2. 對所有的分類樹進行迭代：
    2.1 根據前一輪分類樹的結果更新分類目標的權重值（被錯誤分類的有更高的權重）
    2.2 用訓練的子樣本建模
    2.3 用所得模型對所有的樣本進行預測
    2.4 再次根據分類結果更新權重值
3. 返回最終結果

以上步驟是一個極度簡化的BGM模型，而目前我們所提到的引數會影響2.2這一步，即建模的過程。現在我們來看看影響boosting過程的引數：

1. learning_ rate
   
   • 這個引數決定著每一個決定樹對於最終結果（步驟2.4）的影響。GBM設定了初始的權重值之後，每一次樹分類都會更新這個值，而learning_ rate控制著每次更新的幅度。
   • 一般來說這個值不應該設的比較大，因為較小的learning rate使得模型對不同的樹更加穩健，就能更好地綜合它們的結果。
2. n_ estimators
   
   • 定義了需要使用到的決定樹的數量（步驟2）
   • 雖然GBM即使在有較多決定樹時仍然能保持穩健，但還是可能發生過度擬合。所以也需要針對learning rate用CV值檢驗。

3. subsample

   • 訓練每個決定樹所用到的子樣本佔總樣本的比例，而對於子樣本的選擇是隨機的。
   • 用稍小於1的值能夠使模型更穩健，因為這樣減少了方差。
   • 一把來說用~0.8就行了，更好的結果可以用調參獲得。

   好了，現在我們已經介紹了樹引數和boosting引數，此外還有第三類引數，它們能影響到模型的總體功能：

4. loss

   • 指的是每一次節點分裂所要最小化的損失函式(loss function)
   • 對於分類和迴歸模型可以有不同的值。一般來說不用更改，用預設值就可以了，除非你對它及它對模型的影響很清楚。
5. init
   
   • 它影響了輸出引數的起始化過程
   • 如果我們有一個模型，它的輸出結果會用來作為GBM模型的起始估計，這個時候就可以用init
6. random_ state
   
   • 作為每次產生隨機數的隨機種子
   • 使用隨機種子對於調參過程是很重要的，因為如果我們每次都用不同的隨機種子，即使引數值沒變每次出來的結果也會不同，這樣不利於比較不同模型的結果。
   • 任一個隨即樣本都有可能導致過度擬合，可以用不同的隨機樣本建模來減少過度擬合的可能，但這樣計算上也會昂貴很多，因而我們很少這樣用
7. verbose
   
   • 決定建模完成後對輸出的列印方式：
     
     • 0：不輸出任何結果（預設）
     • 1：列印特定區域的樹的輸出結果
     • >1：列印所有結果
8. warm_ start
   
   • 這個引數的效果很有趣，有效地使用它可以省很多事
   • 使用它我們就可以用一個建好的模型來訓練額外的決定樹，能節省大量的時間，對於高階應用我們應該多多探索這個選項。
9. presort
   
   • 決定是否對資料進行預排序，可以使得樹分裂地更快。
   • 預設情況下是自動選擇的，當然你可以對其更改

我知道我列了太多的引數，所以我在我的GitHub裡整理出了一張表，可以直接下載：GitHub地址

5.引數調節例項

• City這個變數已經被我捨棄了，因為有太多種類了。
• DOB轉為Age|DOB,捨棄了DOB
• 建立了EMI_Loan_Submitted_Missing這個變數，當EMI_Loan_Submitted 變數值缺失時它的值為1，否則為0。然後捨棄了EMI_Loan_Submitted。
• EmployerName的值也太多了，我把它也捨棄了
• Existing_EMI的缺失值被填補為0（中位數），因為只有111個缺失值
• 建立了Interest_Rate_Missing變數，類似於#3，當Interest_Rate有值時它的值為0，反之為1，原來的Interest_Rate變數被捨棄了
• Lead_Creation_Date也被捨棄了，因為對結果看起來沒什麼影響
• 用Loan_Amount_Applied和 Loan_Tenure_Applied的中位數填補了缺失值
• 建立了Loan_Amount_Submitted_Missing變數，當Loan_Amount_Submitted有缺失值時為1，反之為0，原本的Loan_Amount_Submitted變數被捨棄
• 建立了Loan_Tenure_Submitted_Missing變數，當Loan_Tenure_Submitted有缺失值時為1，反之為0，原本的Loan_Tenure_Submitted變數被捨棄
• 捨棄了LoggedIn,和Salary_Account
• 建立了Processing_Fee_Missing變數，當Processing_Fee有缺失值時為1，反之為0，原本的Processing_Fee變數被捨棄
• Source-top保留了2個，其他組合成了不同的類別
• 對一些變數採取了數值化和獨熱編碼（One-Hot-Coding）操作

你們可以從GitHub裡data_preparation iPython notebook中看到這些改變。

首先，我們載入需要的library和資料：

#Import libraries:
import pandas as pd
import numpy as np
from sklearn.ensemble import GradientBoostingClassifier  #GBM algorithm
from sklearn import cross_validation, metrics   #Additional scklearn functions
from sklearn.grid_search import GridSearchCV   #Perforing grid search

import matplotlib.pylab as plt
%matplotlib inline
from matplotlib.pylab import rcParams
rcParams['figure.figsize'] = 12, 4

train = pd.read_csv('train_modified.csv')
target = 'Disbursed'
IDcol = 'ID'

然後我們來寫一個建立GBM模型和CV值的函式。

def modelfit(alg, dtrain, predictors, performCV=True, printFeatureImportance=True, cv_folds=5):
    #Fit the algorithm on the data
    alg.fit(dtrain[predictors], dtrain['Disbursed'])

    #Predict training set:
    dtrain_predictions = alg.predict(dtrain[predictors])
    dtrain_predprob = alg.predict_proba(dtrain[predictors])[:,1]

    #Perform cross-validation:
    if performCV:
        cv_score = cross_validation.cross_val_score(alg, dtrain[predictors], dtrain['Disbursed'], cv=cv_folds, scoring='roc_auc')

    #Print model report:
    print "\nModel Report"
    print "Accuracy : %.4g" % metrics.accuracy_score(dtrain['Disbursed'].values, dtrain_predictions)
    print "AUC Score (Train): %f" % metrics.roc_auc_score(dtrain['Disbursed'], dtrain_predprob)

    if performCV:
        print "CV Score : Mean - %.7g | Std - %.7g | Min - %.7g | Max - %.7g" % (np.mean(cv_score),np.std(cv_score),np.min(cv_score),np.max(cv_score))

    #Print Feature Importance:
    if printFeatureImportance:
        feat_imp = pd.Series(alg.feature_importances_, predictors).sort_values(ascending=False)
        feat_imp.plot(kind='bar', title='Feature Importances')
        plt.ylabel('Feature Importance Score')

接著就要建立一個基線模型（baseline model）。這裡我們用AUC來作為衡量標準，所以用常數的話AUC就是0.5。一般來說用預設引數設定的GBM模型就是一個很好的基線模型，我們來看看這個模型的輸出和特徵重要性：

#Choose all predictors except target & IDcols
predictors = [x for x in train.columns if x not in [target, IDcol]]
gbm0 = GradientBoostingClassifier(random_state=10)
modelfit(gbm0, train, predictors)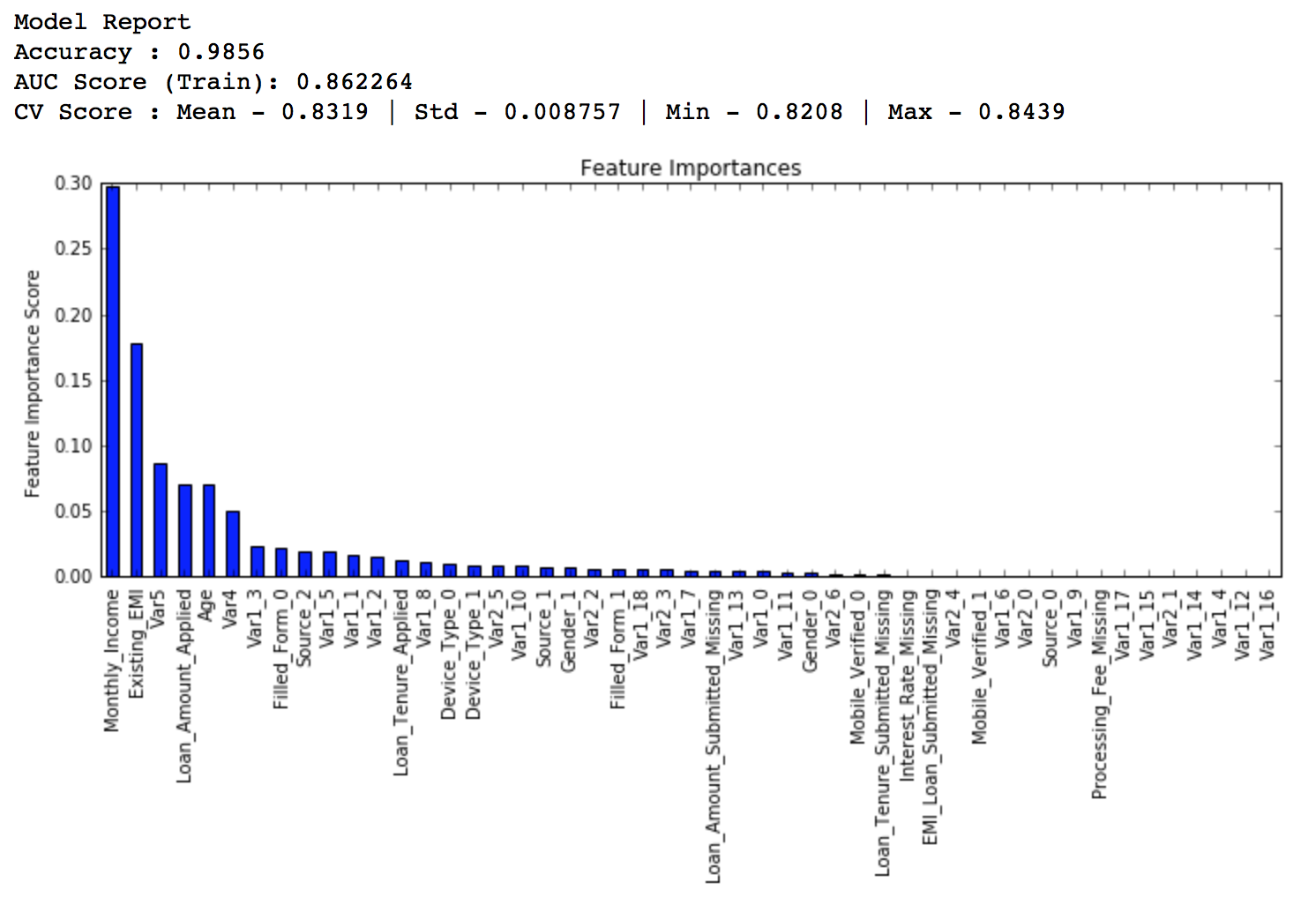

從圖上看出，CV的平均值是0.8319，後面調整的模型會做得比這個更好。

5.1 引數調節的一般方法

之前說過，我們要調節的引數有兩種：樹引數和boosting引數。learning rate沒有什麼特別的調節方法，因為只要我們訓練的樹足夠多learning rate總是小值來得好。

雖然隨著決定樹的增多GBM並不會明顯得過度擬合，高learing rate還是會導致這個問題，但如果我們一味地減小learning rate、增多樹,計算就會非常昂貴而且需要執行很長時間。瞭解了這些問題，我們決定採取以下方法調參：

1. 選擇一個相對來說稍微高一點的learning rate。一般預設的值是0.1，不過針對不同的問題，0.05到0.2之間都可以
2. 決定當前learning rate下最優的決定樹數量。它的值應該在40-70之間。記得選擇一個你的電腦還能快速執行的值，因為之後這些樹會用來做很多測試和調參。
3. 接著調節樹引數來調整learning rate和樹的數量。我們可以選擇不同的引數來定義一個決定樹，後面會有這方面的例子
4. 降低learning rate，同時會增加相應的決定樹數量使得模型更加穩健

5.2固定 learning rate和需要估測的決定樹數量

為了決定boosting引數，我們得先設定一些引數的初始值，可以像下面這樣：

1. min_ samples_ split=500: 這個值應該在總樣本數的0.5-1%之間，由於我們研究的是不均等分類問題，我們可以取這個區間裡一個比較小的數，500。
2. min_ samples_ leaf=50: 可以憑感覺選一個合適的數，只要不會造成過度擬合。同樣因為不均等分類的原因，這裡我們選擇一個比較小的值。
3. max_ depth=8: 根據觀察數和自變數數，這個值應該在5-8之間。這裡我們的資料有87000行，49列，所以我們先選深度為8。
4. max_ features=’sqrt’: 經驗上一般都選擇平方根。
5. subsample=0.8: 開始的時候一般就用0.8

注意我們目前定的都是初始值，最終這些引數的值應該是多少還要靠調參決定。現在我們可以根據learning rate的預設值0.1來找到所需要的最佳的決定樹數量，可以利用網格搜尋（grid search）實現，以10個數遞增，從20測到80。

#Choose all predictors except target & IDcols
predictors = [x for x in train.columns if x not in [target, IDcol]]
param_test1 = {'n_estimators':range(20,81,10)}
gsearch1 = GridSearchCV(estimator = GradientBoostingClassifier(learning_rate=0.1, min_samples_split=500,min_samples_leaf=50,max_depth=8,max_features='sqrt',subsample=0.8,random_state=10), 
param_grid = param_test1, scoring='roc_auc',n_jobs=4,iid=False, cv=5)
gsearch1.fit(train[predictors],train[target])

來看一下輸出結果：

gsearch1.grid_scores_, gsearch1.best_params_, gsearch1.best_score_

可以看出對於0.1的learning rate, 60個樹是最佳的，而且60也是一個合理的決定樹數量，所以我們就直接用60。但在一些情況下上面這段程式碼給出的結果可能不是我們想要的，比如：

1. 如果給出的輸出是20，可能就要降低我們的learning rate到0.05，然後再搜尋一遍。
2. 如果輸出值太高，比如100，因為調節其他引數需要很長時間，這時候可以把learniing rate稍微調高一點。

5.3 調節樹引數

樹引數可以按照這些步驟調節：

1. 調節max_depth和 num_samples_split
2. 調節min_samples_leaf
3. 調節max_features

需要注意一下調參順序，對結果影響最大的引數應該優先調節，就像max_depth和num_samples_split。

重要提示：接著我會做比較久的網格搜尋(grid search)，可能會花上15-30分鐘。你在自己嘗試的時候應該根據電腦情況適當調整需要測試的值。

max_depth可以相隔兩個數從5測到15，而min_samples_split可以按相隔200從200測到1000。這些完全憑經驗和直覺，如果先測更大的範圍再用迭代去縮小範圍也是可行的。

param_test2 = {'max_depth':range(5,16,2), 'min_samples_split':range(200,1001,200)}
gsearch2 = GridSearchCV(estimator = GradientBoostingClassifier(learning_rate=0.1, n_estimators=60, max_features='sqrt', subsample=0.8, random_state=10), 
param_grid = param_test2, scoring='roc_auc',n_jobs=4,iid=False, cv=5)
gsearch2.fit(train[predictors],train[target])
gsearch2.grid_scores_, gsearch2.best_params_, gsearch2.best_score_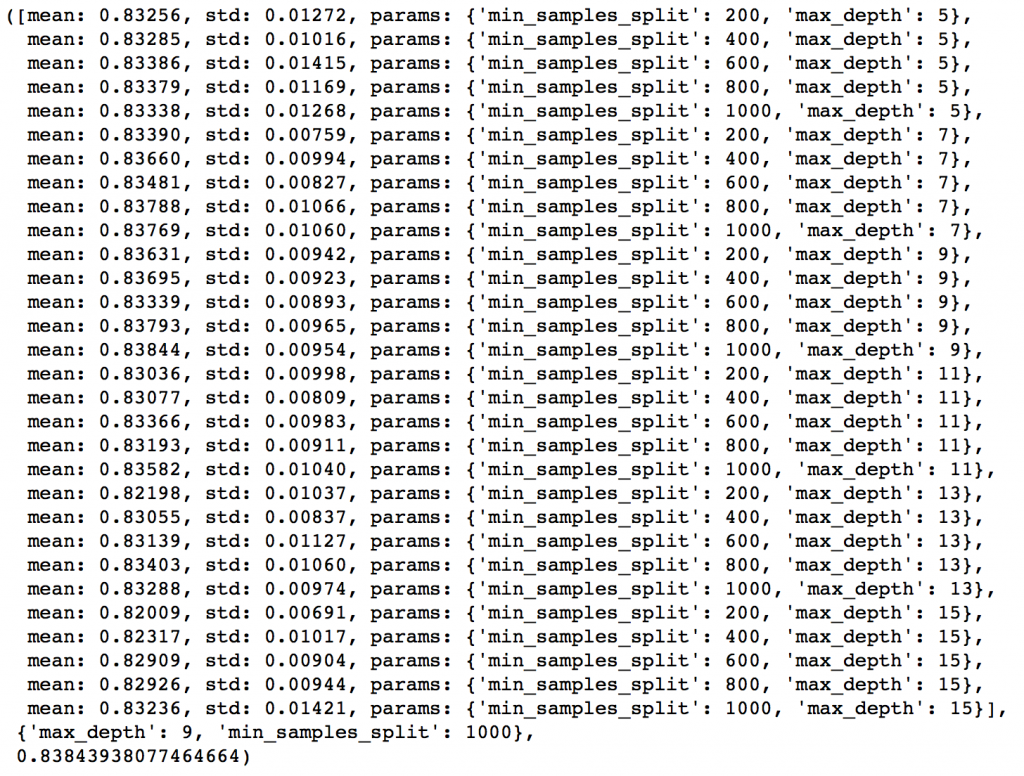

從結果可以看出，我們從30種組合中找出最佳的max_depth是9，而最佳的min_smaples_split是1000。1000是我們設定的範圍裡的最大值，有可能真正的最佳值比1000還要大，所以我們還要繼續增加min_smaples_split。樹深就用9。接著就來調節min_samples_leaf，可以測30，40，50，60，70這五個值，同時我們也試著調大min_samples_leaf的值。

param_test3 = {'min_samples_split':range(1000,2100,200), 'min_samples_leaf':range(30,71,10)}
gsearch3 = GridSearchCV(estimator = GradientBoostingClassifier(learning_rate=0.1, n_estimators=60,max_depth=9,max_features='sqrt', subsample=0.8, random_state=10), 
param_grid = param_test3, scoring='roc_auc',n_jobs=4,iid=False, cv=5)
gsearch3.fit(train[predictors],train[target])
gsearch3.grid_scores_, gsearch3.best_params_, gsearch3.best_score_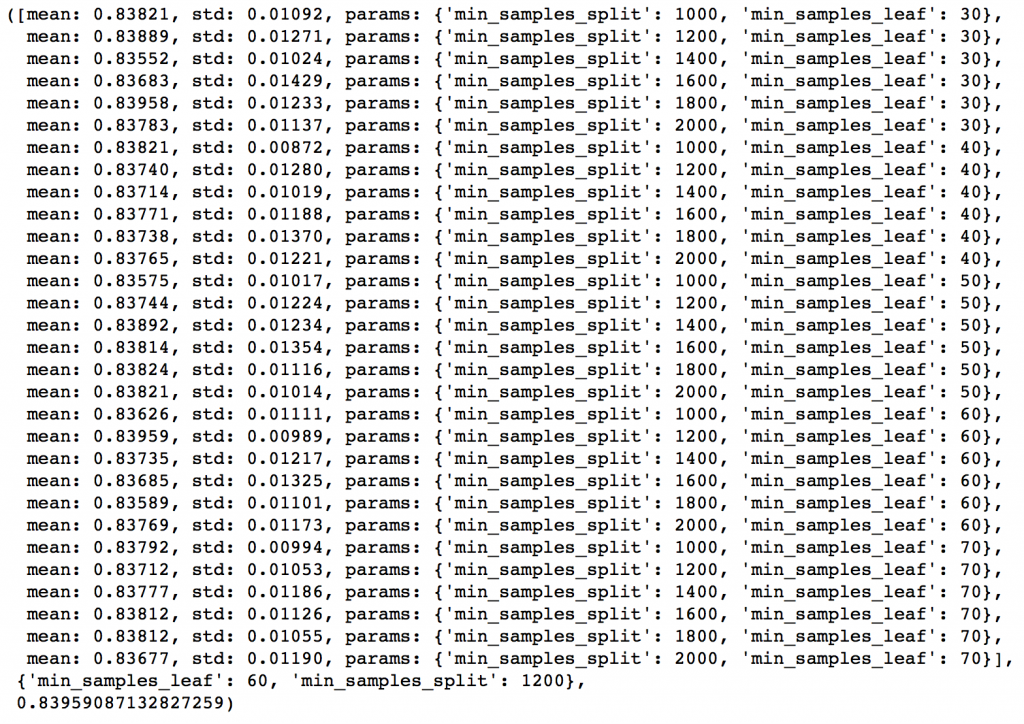

這樣min_samples_split的最佳值是1200，而min_samples_leaf的最佳值是60。注意現在CV值增加到了0.8396。現在我們就根據這個結果來重新建模，並再次評估特徵的重要性。

modelfit(gsearch3.best_estimator_, train, predictors)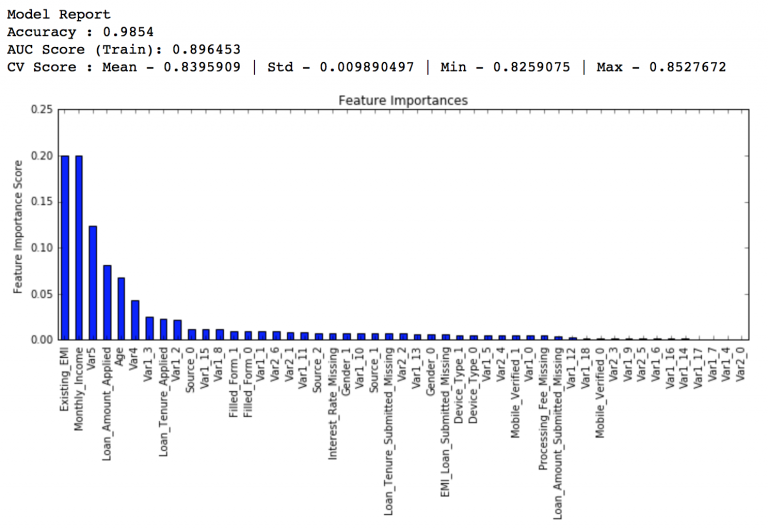

比較之前的基線模型結果可以看出，現在我們的模型用了更多的特徵，並且基線模型裡少數特徵的重要性評估值過高，分佈偏斜明顯，現在分佈得更加均勻了。

接下來就剩下最後的樹引數max_features了，可以每隔兩個數從7測到19。

param_test4 = {'max_features':range(7,20,2)}
gsearch4 = GridSearchCV(estimator = GradientBoostingClassifier(learning_rate=0.1, n_estimators=60,max_depth=9, min_samples_split=1200, min_samples_leaf=60, subsample=0.8, random_state=10),
param_grid = param_test4, scoring='roc_auc',n_jobs=4,iid=False, cv=5)
gsearch4.fit(train[predictors],train[target])
gsearch4.grid_scores_, gsearch4.best_params_, gsearch4.best_score_

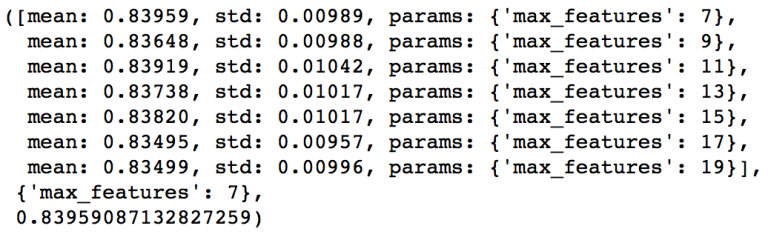
最佳的結果是7，正好就是我們設定的初始值（平方根）。當然你可能還想測測小於7的值，我也鼓勵你這麼做。而按照我們的設定，現在的樹引數是這樣的：

• min_samples_split: 1200
• min_samples_leaf: 60
• max_depth: 9
• max_features: 7

5.4 調節子樣本比例來降低learning rate

接下來就可以調節子樣本佔總樣本的比例，我準備嘗試這些值：0.6,0.7,0.75,0.8,0.85,0.9。

param_test5 = {'subsample':[0.6,0.7,0.75,0.8,0.85,0.9]}
gsearch5 = GridSearchCV(estimator = GradientBoostingClassifier(learning_rate=0.1, n_estimators=60,max_depth=9,min_samples_split=1200, min_samples_leaf=60, subsample=0.8, random_state=10,max_features=7),
param_grid = param_test5, scoring='roc_auc',n_jobs=4,iid=False, cv=5)
gsearch5.fit(train[predictors],train[target])
gsearch5.grid_scores_, gsearch5.best_params_, gsearch5.best_score_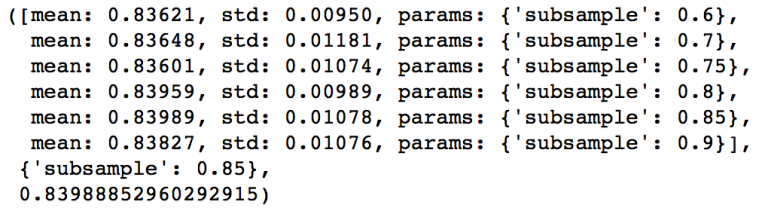

給出的結果是0.85。這樣所有的引數都設定好了，現在我們要做的就是進一步減少learning rate，就相應地增加了樹的數量。需要注意的是樹的個數是被動改變的，可能不是最佳的，但也很合適。隨著樹個數的增加，找到最佳值和CV的計算量也會加大，為了看出模型執行效率，我還提供了我每個模型在比賽的排行分數（leaderboard score），怎麼得到這個資料不是公開的，你很難重現這個數字，它只是為了更好地幫助我們理解模型表現。

現在我們先把learning rate降一半，至0.05，這樣樹的個數就相應地加倍到120。

predictors = [x for x in train.columns if x not in [target, IDcol]]
gbm_tuned_1 = GradientBoostingClassifier(learning_rate=0.05, n_estimators=120,max_depth=9, min_samples_split=1200,min_samples_leaf=60, subsample=0.85, random_state=10, max_features=7)
modelfit(gbm_tuned_1, train, predictors)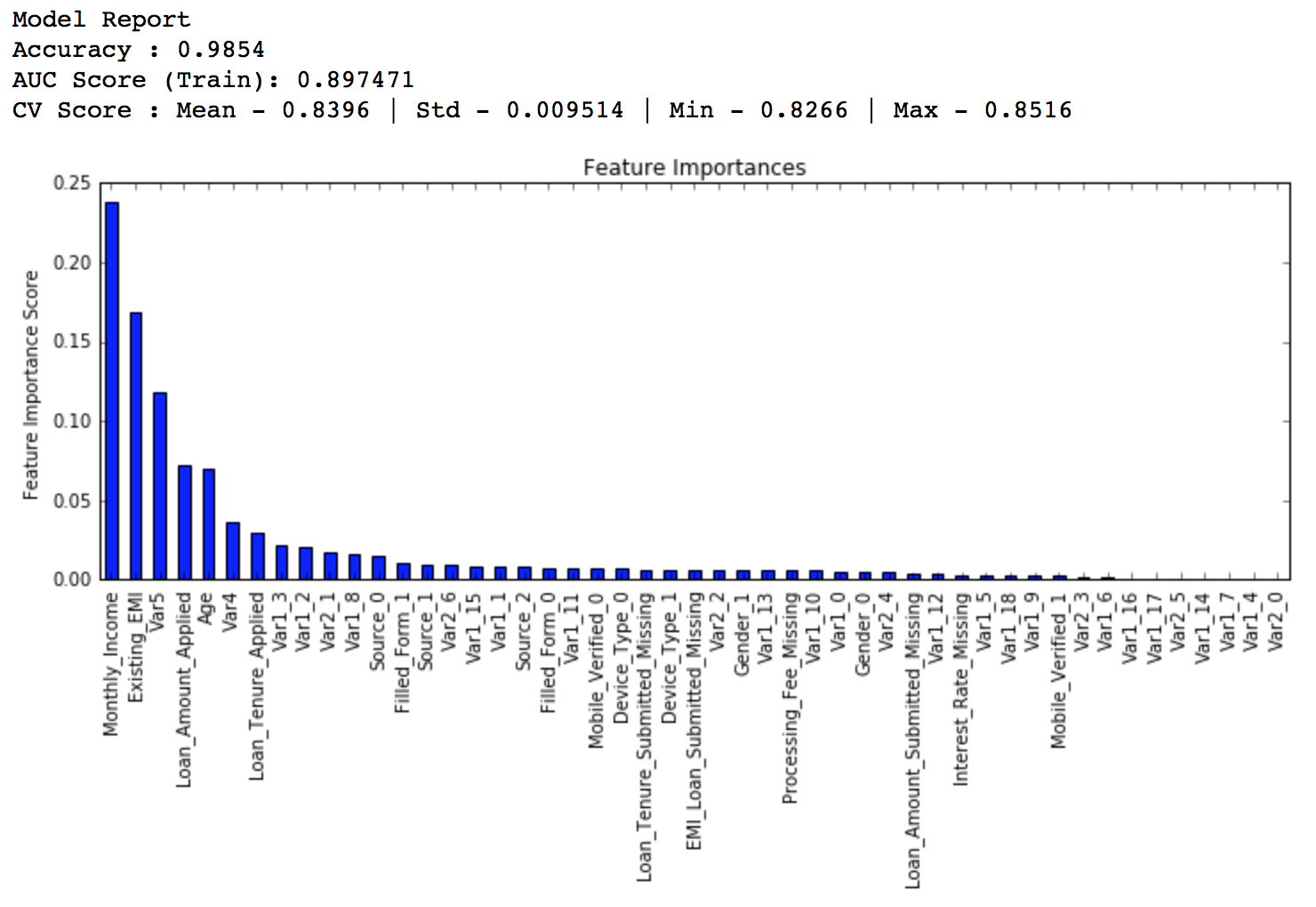

排行得分：0.844139

接下來我們把learning rate進一步減小到原值的十分之一,即0.01，相應地，樹的個數變為600。

predictors = [x for x in train.columns if x not in [target, IDcol]]
gbm_tuned_2 = GradientBoostingClassifier(learning_rate=0.01, n_estimators=600,max_depth=9, min_samples_split=1200,min_samples_leaf=60, subsample=0.85, random_state=10, max_features=7)
modelfit(gbm_tuned_2, train, predictors)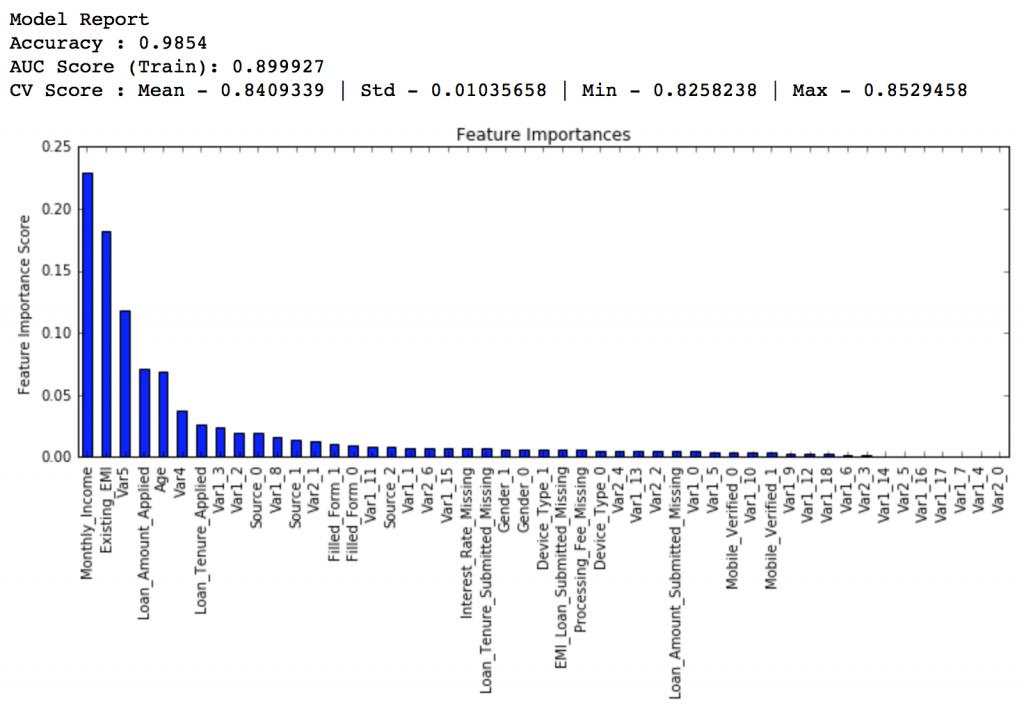

排行得分：0.848145

繼續把learning rate縮小至二十分之一，即0.005,這時候我們有1200個樹。

predictors = [x for x in train.columns if x not in [target, IDcol]]
gbm_tuned_3 = GradientBoostingClassifier(learning_rate=0.005, n_estimators=1200,max_depth=9, min_samples_split=1200, min_samples_leaf=60, subsample=0.85, random_state=10, max_features=7,
warm_start=True)
modelfit(gbm_tuned_3, train, predictors, performCV=False)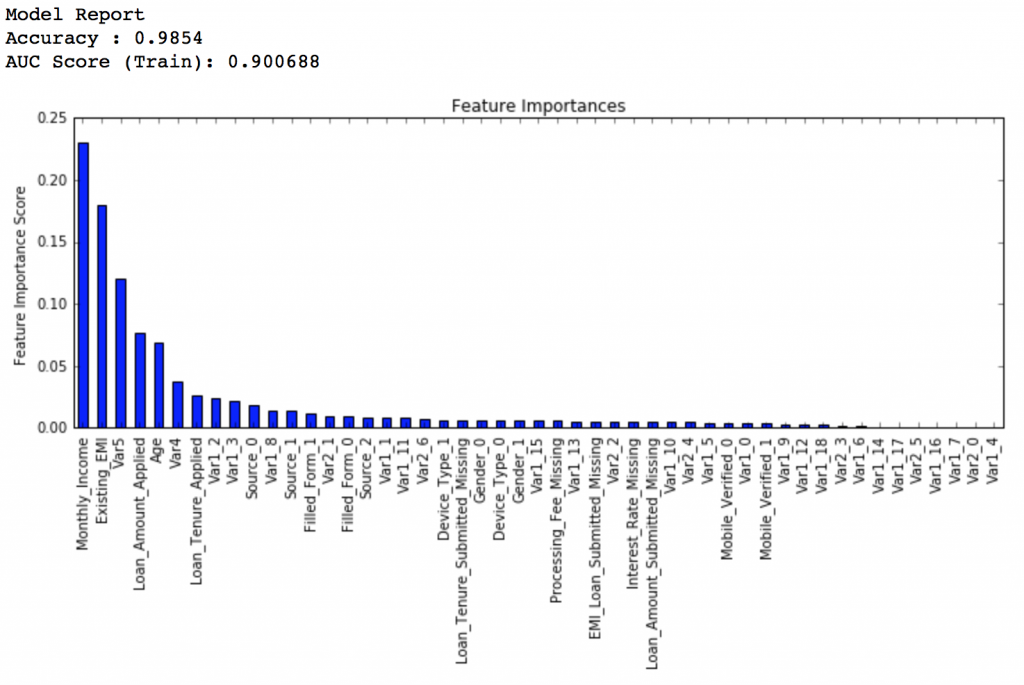

排行得分：0.848112

排行得分稍微降低了，我們停止減少learning rate，只單方面增加樹的個數，試試1500個樹。

predictors = [x for x in train.columns if x not in [target, IDcol]]
gbm_tuned_4 = GradientBoostingClassifier(learning_rate=0.005, n_estimators=1500,max_depth=9, min_samples_split=1200, min_samples_leaf=60, subsample=0.85, random_state=10, max_features=7,
warm_start=True)
modelfit(gbm_tuned_4, train, predictors, performCV=False)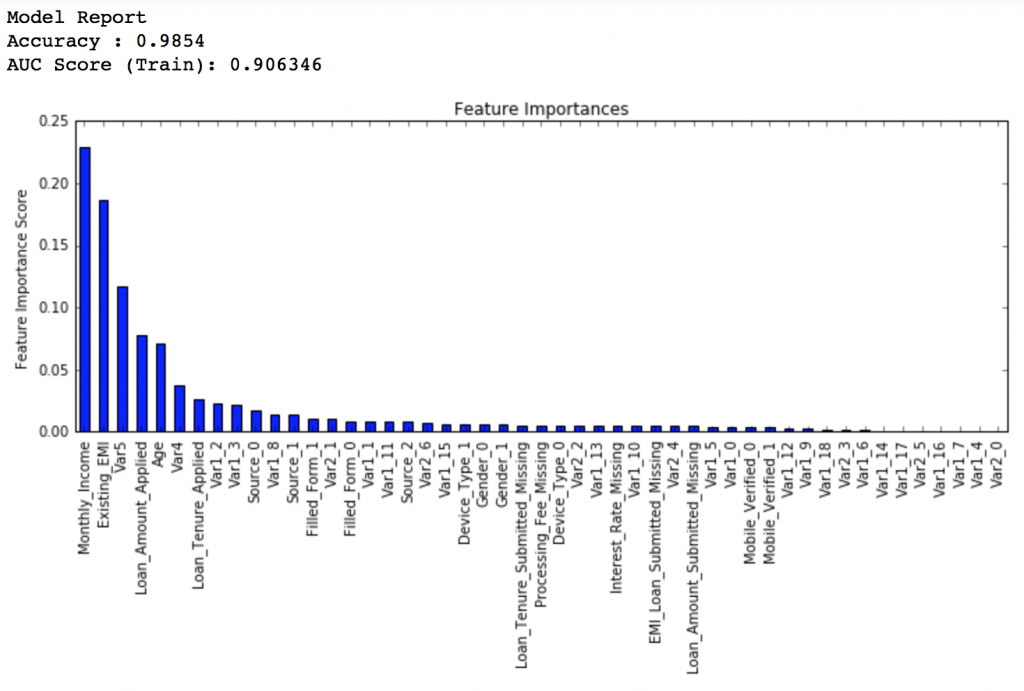

排行得分：0.848747

看，就這麼簡單，排行得分已經從0.844升高到0.849了，這可是一個很大的提升。

還有一個技巧就是用“warm_start”選項。這樣每次用不同個數的樹都不用重新開始。所有的程式碼都可以從我的Github裡下載到。

6.總結

這篇文章詳細地介紹了GBM模型。我們首先了解了何為boosting，然後詳細介紹了各種引數。 這些引數可以被分為3類：樹引數，boosting引數，和其他影響模型的引數。最後我們提到了用GBM解決問題的 一般方法，並且用AV Data Hackathon 3.x problem資料運用了這些方法。最後，希望這篇文章確實幫助你更好地理解了GBM，在下次運用GBM解決問題的時候也更有信心。