一些演算法的MapReduce實現——矩陣分塊乘法計算(1)
阿新 • • 發佈:2019-02-17
矩陣分塊簡介
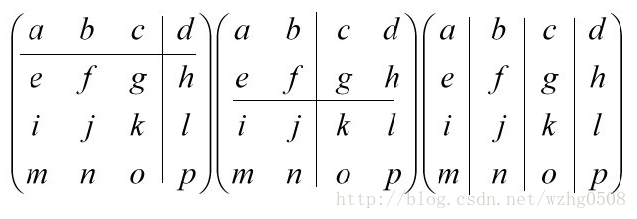
一個分塊矩陣(分段矩陣)就是將矩陣分割出較小的矩形矩陣,這些較小的矩陣就稱為區塊。換個方式來說,就是以較小的矩陣組合成一個矩陣。通過將大的矩陣通過分塊的方式劃分,並將每個分塊(稱為子塊)看做另一個矩陣的元素,這樣之後再參與運算,通常可以簡化運算。例如,有的大矩陣可以通過分塊變為對角矩陣或者是三角矩陣等特殊形式的矩陣。分塊矩陣的分割原則是以水平線和垂直線進行劃分:
分塊矩陣的運演算法則:
(i)對於加法,數乘,矩陣乘法就是對每個子塊執行對應的操作
(ii)對於加法要注意分塊的時候要確保對應子塊的行列數要相同也就是要用相同的方法分塊.
設矩陣A和B的行列數相同,並採用相同的分塊法分成:
若A和B的對應字塊有相同行列號則:
(iii)對於矩陣乘法要注意對應子塊要確保相乘是有意義的(第一個子塊的列數等於第二個的行數)
設A為m × l矩陣 , B為l × n矩陣 ,分塊成:
(iii)對於矩陣乘法要注意對應子塊要確保相乘是有意義的(第一個子塊的列數等於第二個的行數)
設A為m × l矩陣 , B為l × n矩陣 ,分塊成:
分塊法計算例項
AB如上分塊
其中
令

後續再補上一些演算法的MapReduce實現——矩陣分塊計算(2)
參考