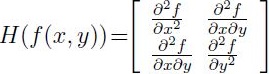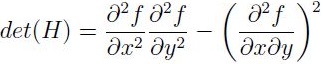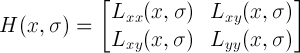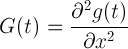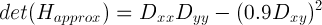【影象分析】SURF特徵提取分析
基本介紹
首先,我們引用[3]中對SURF描述為:“SURF (Speeded Up Robust Features)isa robust local feature detector, first presented by Herbert Bay et al. in 2006, that can be
used in computer vision tasks likeobject recognition or 3D reconstruction. It is partly inspired by the SIFT descriptor.The standard version of SURF is several times faster than SIFT and claimed
by its authors to be more robust against different image transformations than SIFT
從上述對SURF描述,可知:第一、SURF演算法是對SIFT演算法加強版,同時加速的具有魯棒性的特徵。第二、標準的SURF運算元比SIFT運算元快好幾倍,並且在多幅圖片下具有更好的魯棒性。SURF最大的特徵在於採用了harr特徵以及積分影象integral image的概念,這大大加快了程式的執行時間。
演算法描述
為了實現尺度不變性的特徵點檢測與匹配,SURF演算法則先利用Hessian矩陣確定候選點,然後進行非極大抑制,計算複雜度降低多了。整個演算法由以下幾個部分組成。
1.Hessian黑森矩陣構建
我們知道:SIFT演算法建立一幅影象的金字塔,在每一層進行高斯濾波並求取影象差(DOG)進行特徵點的提取,而SURF則用的是Hessian Matrix進行特徵點的提取,所以黑森矩陣是SURF演算法的核心。假設函式f(x,y),Hessian矩陣H是由函式偏導陣列成。首先來看看影象中某個畫素點的Hessian
Matrix的定義為:
從而每一個畫素點都可以求出一個Hessian Matrix. Hessian矩陣判別式為:
判別式的值是H矩陣的特徵值,可以利用判定結果的符號將所有點分類,根據判別式取值正負,從來判別該點是或不是極點的值。在SURF演算法中,通常用影象畫素I(x,y)取代函式值f(x,y)。然後選用二階標準高斯函式作為濾波器。通過特定核間的卷積計算二階偏導數,這樣便能計算出H矩陣的三個矩陣元素Lxx, Lxy, Lyy,從而計算出H矩陣公式如下:
但是由於我們的特徵點需要尺度無關性,所以在進行Hessian矩陣構造前,需要對其進行高斯濾波。這樣,經過濾波後在進行Hessian的計算,其公式如下:
L(x,t)是一幅影象在不同解析度下的表示,可以利用高斯核G(t)與影象函式I(x)在點x的卷積來實現,其中高斯核G(t)為:
其中g(t)為高斯函式,t 為高斯方差。通過這種方法可以為影象中每個畫素計算出其H矩陣的決定值,並用這個值來判別特徵點。為此Herbert Bay提出用近似值現代替L(x,t)。為平衡準確值與近似值間的誤差引入權值。權值隨尺度變化,則H矩陣判別式可表示為:
其中為何式中0.9呢.請詳見[1]。因求Hessian時要先高斯平滑,然後求其二階導數,這在離散的畫素是用模板卷積形
成的。這比如說y方向上的模板Fig1(a)和Fig1(c).Fig1(a)即用高斯平滑後在y方向上求二階導數的模板。為了加快運算用了近似處理,其處理結果如Fig1(b)所 示,這樣就簡化了很多。並且可以採用積分圖來運算,大大的加快了速度。同理,x和y方向的二階混合偏導模板Fig1(b)與Fig1(d)。
2. 尺度空間生成
影象的尺度空間是這幅影象在不同解析度下的表示。上面講的這麼多隻是得到了一張近似Hessian行列式圖,這類似SIFT中的DOG圖,但是在金字塔影象中分為很多層,每一層叫做一個octave,每一個octave中又有幾張尺度不同的
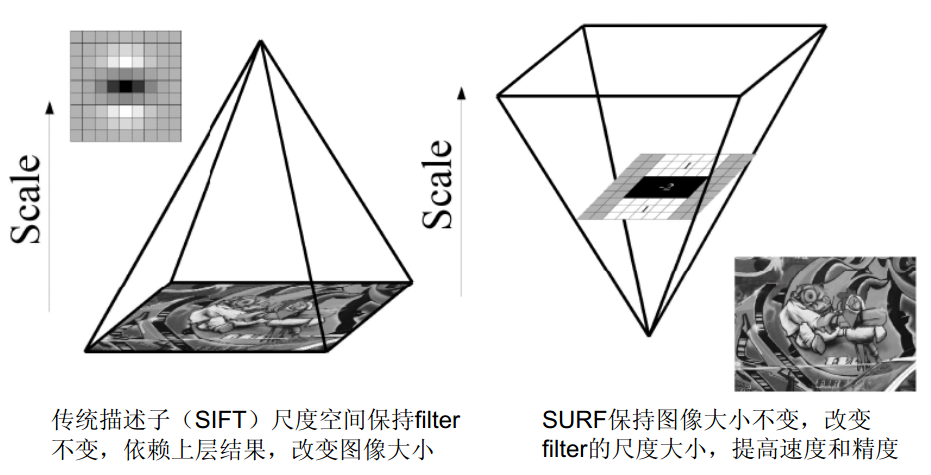
圖片。在SIFT演算法中,同一個octave層中的圖片尺寸(即大小)相同,但是尺度(即模糊程度)不同,而不同的octave層中的圖片尺寸大小也不相同,因為它是由上一層圖片降取樣得到的。在進行高斯模糊時,SIFT的高斯模板大小是始終不變的,只是在不同的octave之間改變圖片的大小。而在SURF中,圖片的大小是一直不變的,不同的octave層得到的待檢測圖片是改變高斯模糊尺寸大小得到的,當然了,同一個octave中個的圖片用到的高斯模板尺度也不同。演算法允許尺度空間多層影象同時被處理,不需對影象進行二次抽樣,從而提高演算法效能。上圖左邊是傳統方式建立一個如圖所示的金字塔結構,影象的寸是變化的,並且運
算會反覆使用高斯函式對子層進行平滑處理,上圖右邊說明SURF演算法使原始影象保持不變而只改變濾波器大小。SURF採用這種方法節省了降取樣過程,其處理速度自然也就提上去了(注:上圖片來自於網路)。
3. 利用非極大值抑制初步確定特徵點和精確定位特徵點
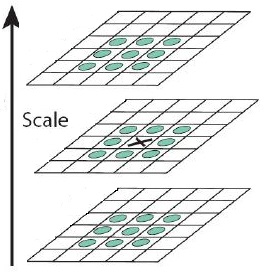
將經過hessian矩陣處理過的每個畫素點與其3維領域的26個點進行大小比較,如果它是這26個點中的最大值或者最小值,則保留下來,當做初步的特徵點。檢測過程中使用與該尺度層影象解析度相對應大小的濾波器進行檢測,以3×3的濾波器為例,該尺度層影象中9個畫素點之一.如下圖中檢測特徵點與自身尺度層中其餘8個點和在其之上及之下的兩個尺度層9個點進行比較,共26個點,圖中標記‘x’的畫素點的特徵值若大於周圍畫素則可確定該點為該區域的特徵點。
然後,採用3維線性插值法得到亞畫素級的特徵點,同時也去掉那些值小於一定閾值的點,增加極值使檢測到的特徵點數量減少,最終只有幾個特徵最強點會被檢測出來。
4. 選取特徵點主方向確定
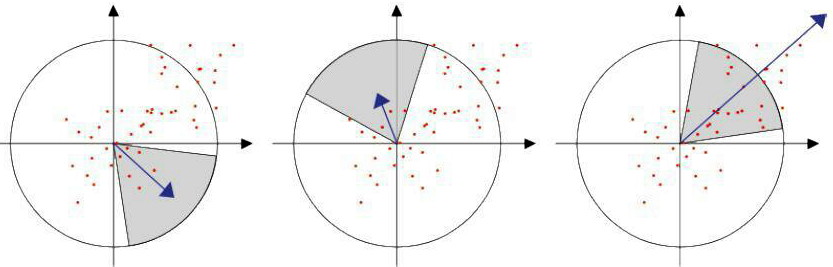
為了保證旋轉不變性,在SURF中,不統計其梯度直方圖,而是統計特徵點領域內的Harr小波特徵。即以特徵點為中心,計算半徑為6s(S為特徵點所在的尺度值)的鄰域內,統計60度扇形內所有點在x(水平)和y(垂直)方向的Haar小波響應總和(Haar小波邊長取4s),並給這些響應值賦高斯權重係數,使得靠近特徵點的響應貢獻大,而遠離特徵點的響應貢獻小,然後60度範圍內的響應相加以形成新的向量,遍歷整個圓形區域,選擇最長向量的方向為該特徵點的主方向。這樣,通過特徵點逐個進行計算,得到每一個特徵點的主方向。該過程的示意圖如下:
5. 構造SURF特徵點描述運算元
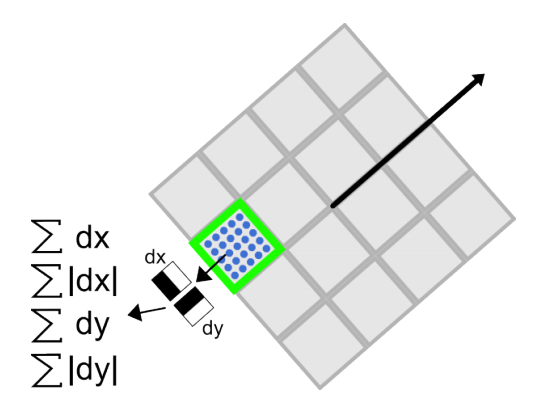
在SURF中,也是在特徵點周圍取一個正方形框,框的邊長為20s(s是所檢測到該特徵點所在的尺度)。該框帶方向,方向當然就是第4步檢測出來的主方向了。然後把該框分為16個子區域,每個子區域統計25個畫素的水平方向和垂直方向的haar小波特徵,這裡的x(水平)和y(垂直)方向都是相對主方向而言的。該haar小波特徵為x(水平)方向值之和,水平方向絕對值之和,垂直方向之和,垂直方向絕對值之和。該過程的示意圖如下所示:
綜上所述,目前,對SURF演算法有了一定了解。所以,可知SURF採用Henssian矩陣獲取影象區域性最值還是十分穩定的,但是在求主方向階段太過於依賴區域性區域畫素的梯度方向,有可能使得找到的主方向不準確,後面的特徵向量提取以及匹配都嚴重依賴於主方向,即使不大偏差角度也可以造成後面特徵匹配的放大誤差,從而匹配不成功;另外影象金字塔的層取得不足夠緊密也會使得尺度有誤差,後面的特徵向量提取同樣依賴相應的尺度,在這個問題上我們只能採用折中解決方法:取適量的層然後進行插值。
實驗結果:
影象特徵提取效果圖如下所示:
影象匹配效果圖所示:
補充思考問題
1. 為什麼選用高斯金字塔來作特徵提取?
首先,採用DOG的金字塔原因是:因為它接近LOG,而LOG的極值點提供了最穩定的特徵,而且DOG方便計算(只要做減法).而LOG的極值點提供的特徵最穩定。其次,我們從直觀理解:特徵明顯的點經過不同尺度的高斯濾波器進行濾波後,差別較大,所以用到的是DOG。但是直觀上怎麼理解呢. 如果相鄰Octave的sigma不是兩倍關係還好理解:如果兩幅影象只是縮放的關係,那麼假設第一個Octave找到了小一倍影象的極值點,那麼大一倍影象的極值點會在下一個Octave找到相似的。但是現在,如果把大一倍影象進行一次下采樣(這樣和小的影象就完全一樣了),進行Gauss濾波時,兩個影象濾波係數(sigma)是不一樣的,不就找不到一樣的極值點了麼.
2.Hessian矩陣為什麼能用來篩選極值點?
SIFT先利用非極大抑制,再用到Hessian矩陣進行濾除。SURF先用Hessian矩陣,再進行非極大抑制。SURF的順序可以加快篩選速度麼(Hessian矩陣濾除的點更多?)至於SURF先用Hessian矩陣,再進行非極大抑制的原因,是不管先極大值抑制還是判斷Hessian矩陣的行列式,金字塔上的點的行列式都是要計算出來的。先判斷是否大於0只要進行1次判斷,而判斷是否是極大值點或者極小值點要與周圍26個點比較,只比較1次肯定快。而在SIFT中,構建的高斯金字塔只有一座(不想SURF是有3座),要進行非極大抑制可以直接用金字塔的結果進行比較。而如果計算Hessian矩陣的行列式,還要再計算Dxx、Dxy、Dyy。因此先進行非極大抑制。這兩個步驟的先後與SIFT/SURF的實際計算情況有關的,都是當前演算法下的最佳順序,而不是說哪種先計算一定更好。
3、為什麼採用梯度特徵作為區域性不變特徵?
這與人的視覺神經相關。採用梯度作為描述子的原因是,人的視覺皮層上的神經元對特定方向和空間頻率的梯度相應很敏感,經過SIFT作者的一些實驗驗證,用梯度的方法進行匹配效果很好。
4、為什麼可以採用某些特徵點的區域性不變特徵進行整幅影象的匹配?
從直觀的人類視覺印象來看,人類視覺對物體的描述也是區域性化的,基於區域性不變特徵的影象識別方法十分接近於人類視覺機理,通過區域性化的特徵組合,形成對目標物體的整體印象,這就為區域性不變特徵提取方法提供了生物學上的解釋,因此區域性不變特徵也得到了廣泛應用。影象中的每個區域性區域的重要性和影響範圍並非同等重要,即特徵不是同等顯著的,其主要理論來源是Marr的計算機視覺理論和Treisman的特徵整合理論,一般也稱為“原子論”。該理論認為視覺的過程開始於對物體的特徵性質和簡單組成部分的分析,是從區域性性質到大範圍性質。SIFT/SURF都是對特徵點的區域性區域的描述,這些特徵點應該是影響重要的點,對這些點的分析更加重要。所以在區域性不變特徵的提取和描述時也遵循與人眼視覺注意選擇原理相類似的機制,所以SIFT/SURF用於匹配有效果。
5. 為什麼Hessian矩陣可以用來判斷極大值/極小值?
在x0點上,hessian矩陣是正定的,且各分量的一階偏導數為0,則x0為極小值點。在x0點上,hessian矩陣是負定的,且各分量的一階偏導數為0,則x0為極大值點。
對於某個區域性區域,若hessian矩陣是半正定的,則這個區域是凸的(反之依然成立);若負定,則這個區域是凹的(反之依然成立)。而對於正定和負定來說,Hessian矩陣的行列式總是大於等於0的。反過來就是說:某個點若是極大值/極小值,hessian矩陣的行列式必然要大於等於0,而大於等於0如果是滿足的,這個點不一定是極大值/極小值(還要判斷一階導數)。所以後面還要進行極大值抑制.