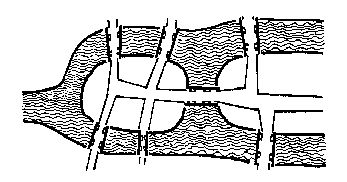
哥尼斯堡是位於普累格河上的一座城市，它包含兩個島嶼及連線它們的七座橋，如下圖所示。

可否走過這樣的七座橋，而且每橋只走過一次？瑞士數學家尤拉(Leonhard Euler，1707—1783)最終解決了這個問題，並由此創立了拓撲學。

這個問題如今可以描述為判斷歐拉回路是否存在的問題。歐拉回路是指不令筆離開紙面，可畫過圖中每條邊僅一次，且可以回到起點的一條迴路。現給定一個無向圖，問是否存在歐拉回路？

輸入格式:

輸入第一行給出兩個正整數，分別是節點數$N$ ($1\le N\le 1000$)和邊數$M$；隨後的$M$行對應$M$條邊，每行給出一對正整數，分別是該條邊直接連通的兩個節點的編號（節點從1到$N$編號）。

輸出格式:

若歐拉回路存在則輸出1，否則輸出0。

輸入樣例1:

6 10
1 2
2 3
3 1
4 5
5 6
6 4
1 4
1 6
3 4
3 6

輸出樣例1:

1

輸入樣例2:

5 8
1 2
1 3
2 3
2 4
2 5
5 3
5 4
3 4

輸出樣例2:

0