deeplearning系列(二)自編碼神經網路
1. Pre_training
神經網路演算法通過反向傳播(back propogation)求得目標函式關於引數的偏導數(或者稱梯度值),然後使用梯度下降法(例如SGD)或者擬牛頓法(例如L-BFGS)等優化演算法求得使目標函式最小化時的引數取值。
由於目標函式非凸的,同時由於深度網路引數之多,又因為反向傳播對初始化的引數十分敏感,如果引數初始值選擇的不好,很容易使目標函式的求解陷入很差的區域性最優解。為了解決這個困難的最佳化問題,提出了pre_training 的方案,即通過pre_training技術使預訓練得到的引數作為反向傳播的起始點。這樣可以使反向傳播的初始搜尋點放在一個比較好的位置,從而保證優化演算法可以收斂到一個比較好的區域性最優解。
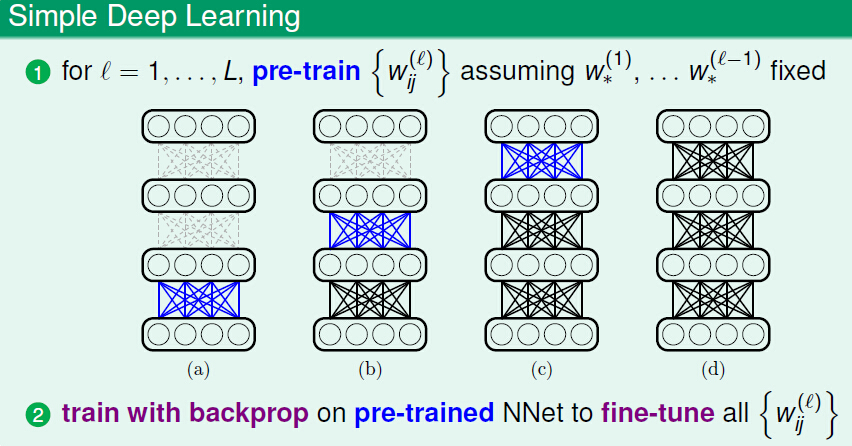
上圖展示了一個簡單的pre_training的流程圖,首先通過逐層pre_training得到每層的引數,然後使用反向傳播來微調(fine-tune)這些預訓練的引數值。
2. 自編碼神經網路
通過神經網路學習的權重引數
好的權重可以:
- 以更精煉的形式(特徵維數減少)儲存前面一層的資訊;
- 同時儘可能少的丟失上一層的資訊(也稱為information-preserving encoding);
- 使用轉換後的特徵還可以很容易地重構出原始的特徵。
自編碼神經網路(Autoencoder)即是一種可以滿足這些要求的pre_training技術。它是一種無監督學習演算法,使用反向傳播,使目標函式的輸出等於輸入值。下圖是一個示例。
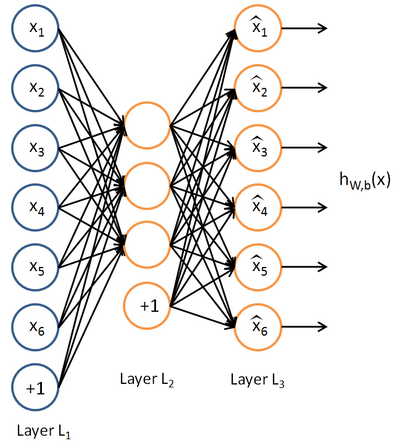
自編碼神經網路試圖逼近這樣的一個恆等函式:
3. 稀疏約束
和包含一個隱藏層的普通神經網路相比,自編碼神經網路除了滿足輸出等於輸入的要求外,還可以加入其它的要求,比如稀疏性約束。
稀疏約束的一種方式可以表示為:啟用函式為sigmoid時,神經元輸出接近於1時可以看做該神經元被啟用,輸出接近於0時看做被抑制。
我們用
表示隱藏神經元
其中,
下圖給出了
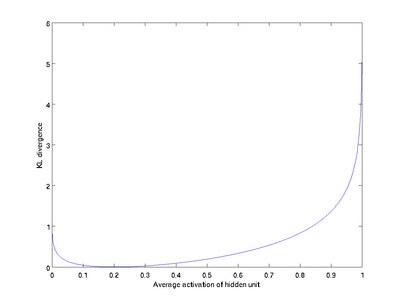
可以看出,只有當
總的目標函式為:
4. 反向傳播
與上一節淺層神經網路相比,反向傳播的不同之處在於殘差的變化:
