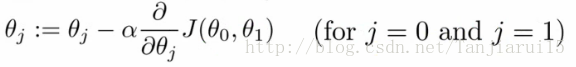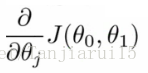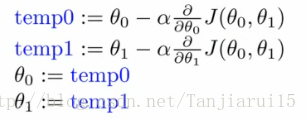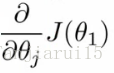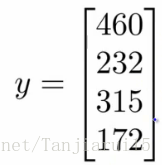coursera《機器學習》吳恩達-week1-03 梯度下降演算法
阿新 • • 發佈:2019-02-18
梯度下降演算法
- 最小化代價函式J
- 梯度下降
- 使用全機學習最小化
- 首先檢視一般的J()函式
- 問題
- 我們有J(θ0, θ1)
- 我們想獲得 min J(θ0, θ1)
- 梯度下降適用於更一般的功能
- J(θ0, θ1, θ2 …. θn)
- min J(θ0, θ1, θ2 …. θn)
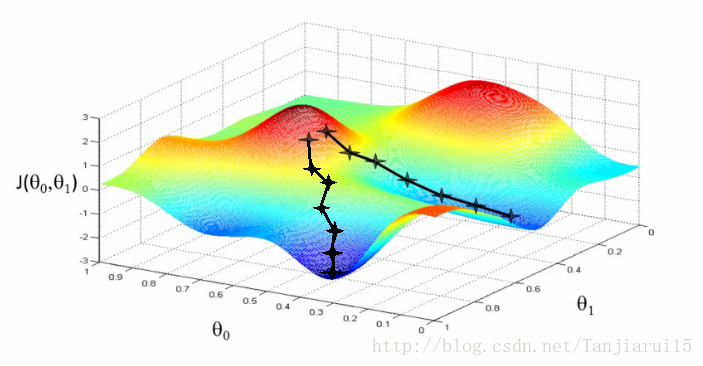
這一演算法如何工作?:
- 從初始假定開始
- 從0,0開始(或任何其他值)
- 保持一點點的改變θ0和θ1,來試圖減少
- 每次更改引數時,可以選擇這降低了梯度J(θ0, θ1)的最可能的
- 重複
- 這樣做直到你收斂到區域性的最低點
- 有一個有趣的性質
- 你開始的位置可以確定你最終的最低點
- 這裡我們可以看到一個初始化點產生一個區域性最小值
- 另一個初始化點產生了另一個區域性最小值
- 你開始的位置可以確定你最終的最低點
更正式的定義
- 重複以下步驟直到收斂
- 這是什麼意思?
- 通過將θj設定為θj減去α倍的區域性成本函式對於θj的導數
- 符號
- :=
- 表示賦值
- NB a = b是 真實斷言
- :=
- α (alpha)
- 是一個叫做學習速率的數字
- 控制你採取的更新速度有多大
- 如果α大,則具有較大的下降幅度
- 如果α小,則幅度較小
- 導數
- 之後詳細解釋 - 一個巧妙的實現梯度下降演算法的實現
- 如下處理θ0和θ1
- For j = 0 and j = 1 意味著同時更新θ0和θ1的值
- 如何實現?
- 為θ0和θ1計算等式右手側
- 所以我們需要一個臨時值
- 然後,更新θ0和θ1的同時
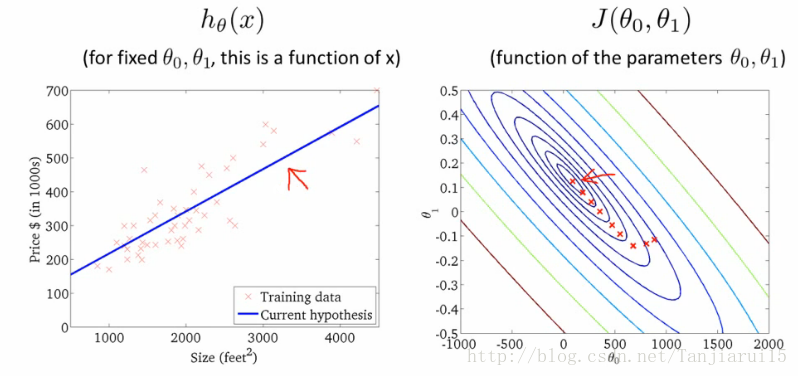
- 我們以圖形方式顯示
- 我們以圖形方式顯示
- 為θ0和θ1計算等式右手側
- 如果您實現非同步更新,則不是梯度下降,並且會出現異常
- 但它可能看起來是對的 - 所以重要的是要記住這一點!
- 瞭解演算法
- 要了解梯度下降,我們將返回一個更簡單的函式,我們最小化一個引數來幫助更詳細地解釋演算法
- 當θ1是一個實數時 ,min θ1 J(θ1)
- 演算法中的兩個關鍵術語
- α(alpha)
- 細微差別
- 偏導與導數
- 當我們有多個變數但是隻相對於一個變數匯出時,使用偏導數
- 當我們相對於所有變數匯出時,使用導數 - 微分項
- 導數說明
- 在這一點做切線並觀察切線斜率
- 所以向下移動會生成一個負導數,α總是正的。因此更新j(θ1) 到一個更小的值。
- 類似的,向上移動會使得j(θ1) 更大
- alpha(α)
- 如果alpha太小或太大,會發生什麼
- 太小
- 步進太小
- 太耗時了
- 太大了
- 可能錯過最小值,最終不能收斂
- 太小
- 如果alpha太小或太大,會發生什麼
- 當你獲得一個區域性最小值
- 此處切線斜率\導數為0
- 因此微分項也為0
- alpha*0=0
- 則θ1=θ1-0
- θ1將保持不變
- 當您接近全域性最小值時,導數項變小,所以即使alpha固定,您的更新也會變小
- 隨著演算法的執行,當您接近最小值時,您將採取較小的步驟
- 所以不需要隨著時間的推移來改變alpha
梯度下降的線性迴歸
- 應用梯度下降來最小化平方差代價函式J(θ0, θ1)
- 現在我們有一個偏導數
- 現在我們展開第一對錶達式、
- J(θ0, θ1) = 1/2m….
- hθ(x) = θ0 + θ1*x
- 當我們需要決定每個引數的導數時:
- When j = 0
- When j = 1
- 標識出針對於θ0和θ1的偏導數
- 當我們根據j = 0和j = 1對這個表示式求導時,我們得到以下結果
- 當我們根據j = 0和j = 1對這個表示式求導時,我們得到以下結果
- 要檢查這個,你需要知道多元微積分
- 所以我們可以將這些值重新插入梯度下降演算法
- 它是如何工作的
- 遇到不同的區域性最優的風險
- 線性迴歸代價函式總是一個凸函式 - 總是有一個最小值
- 碗型曲面
- 一個全域性最優
- 因此梯度下降總會收斂到全域性最優
- 實踐中
- 因此梯度下降總會收斂到全域性最優
- 初始化:
- θ0 = 900
- θ1 = -0.1
- 最終達到全域性最低點
- 這實際上是批量梯度下降
- 指的是在每個步驟中,您可以檢視所有的培訓資料
- 每個步驟計算m個訓練樣例
- 有時,非批次版本存在,它們檢視小資料子集
- 我們將在課程的後面研究其他形式的梯度下降(當m太大時使用)
- 存在用於找到最小函式的解的數值解
- 正則方程 法
- 漸變下降可以更好地擴充套件到大型資料集
- 用於大量的語境和機器學習
下一步 - 重要的擴充套件
兩個演算法的擴充套件
- 數值解的正則方程
- 為了解決[min J(θ0,θ1)]這個最小化問題,我們使用精確地數值方法而不是不斷迭代梯度下降的方法
- 正則方程法
- 有優缺點
- 優點
- 不再是Alpha術語
- 對於一些問題可以快一些
- 壞處
- 更復雜
- 優點
- 我們可以學習更多的功能
我們可以學習更多的函式
- 所以可能有其他引數有助於價格
- 例如與房屋
- 尺寸
- 年齡
- 臥室數字
- 樓層數
- x1,x2,x3,x4
- 例如與房屋
- 有多個功能變得很難繪製
- 不能真正繪製在三維以上
- 符號也變得更加複雜
- 繞過這個最好的方法是線性代數的符號
- 提供符號和一系列可以使用矩陣和向量的事物
- 例如矩陣
- 我們在這裡看到這個矩陣顯示了我們
- 尺寸
- 臥室數量
- 樓層數
- 家庭年齡
- 所有資料都在一個變數中
- 數字塊,將所有資料組織成一個大塊
- 向量
- 顯示為y
- 向我們顯示價格
- 需要線性代數來獲得更復雜的線性迴歸模型
- 線性代數對於製作計算效率高的模型是有好處的(如後所述)
- 提供使用大量資料集的好方法
- 通常,問題的向量化是常見的優化技術