神經網路歐式距離損失函式和softmaxwithloss損失函式轉換示例
1. 神經網路損失函式說明
神經網路歐式距離損失函式用於連續值訓練樣本的擬合,softmaxwithloss損失函式用於分類訓練樣本的擬合。另外,深度網路對於分類樣本的擬合能力強於對於連續值樣本的擬合能力。即同樣的深度網路如果能擬合10組分類的樣本,可能只能擬合3組連續值的樣本。
歐式距離損失函式如下式所示:
(f1)
它在 Logistic Regression
裡其到的作用是講線性預測值轉化為類別概率:假設(f2)是第i個類別的線性預測結果,帶入
Softmax 的結果其實就是先對每一個取 exponential
變成非負,然後除以所有項之和進行歸一化,現在每個
然後 Logistic Regression 的目標函式是根據最大似然原則來建立的,假設資料x所對應的類別為y,則根據我們剛才的計算最大似然就是要最大化Oy的值 (通常是使用 negative log-likelihood 而不是 likelihood,也就是說最小化-log(oy) 的值,這兩者結果在數學上是等價的。)。後面這個操作就是 caffe 文件裡說的 Multinomial Logistic Loss,具體寫出來是這個樣子:
代價函式:
而 Softmax-Loss
其實就是把兩者結合到一起,只要把
softmaxloss損失函式:
注意,這裡的log代表ln的意思,即:=。

其中,y為影象所屬於的類別編號,是真實的標籤值;z為影象所對應的資料,這個資料也是輸入softmax層的資料,這個資料是深度神經網路輸出的資料。
沒有任何 fancy
的東西。比如如果我們要寫一個 Logistic Regression
的 solver,那麼因為要處理的就是這個東西,比較自然地就可以將整個東西合在一起來考慮,或者甚至將(f2)的定義直接一起帶進去然後對w和b進行求導來得到
Gradient Descent 的
反過來,如果是在設計 Deep Neural Networks 的庫,則可能會傾向於將兩者分開來看待:因為 Deep Learning 的模型都是一層一層疊起來的結構,一個計算庫的主要工作是提供各種各樣的 layer,然後讓使用者可以選擇通過不同的方式來對各種 layer 組合得到一個網路層級結構就可以了。比如使用者可能最終目的就是得到各個類別的概率似然值,這個時候就只需要一個 Softmax Layer,而不一定要進行 Multinomial Logistic Loss 操作;或者是使用者有通過其他什麼方式已經得到了某種概率似然值,然後要做最大似然估計,此時則只需要後面的 Multinomial Logistic Loss 而不需要前面的 Softmax 操作。因此提供兩個不同的 Layer 結構比只提供一個合在一起的 Softmax-Loss Layer 要靈活許多。從程式碼的角度來說也顯得更加模組化。但是這裡自然地就出現了一個問題:numerical stability。
讓我們回到 Softmax-Loss
層,由於該層沒有引數,我們只需要計算向後傳遞的導數就可以了,此外由於該層是最頂層,所以不用使用
chain rule 就可以直接計算對於最終輸出(loss)的導數。回憶一下我們剛才的
notation,Softmax-Loss
層合在一起的時候我們用(f5)來表示,它有兩個輸入,一個是
true label,直接來自於最底部的資料層,並且我們不需要對資料層做任何的 gradient descent
引數更新,所以我們不需要像那個輸入進行 back propagation,但是另外一個輸入z則來自於下面的計算層,對於
Logistic Regression 或者普通的 DNNs
下面會是一個全連通的線性內積層,不過具體是什麼我們也不需要關心,只要把
(f6)計算出來丟給下面讓他們自己去算後面的就好了。根據普通的微積分知識,我們很容易算出:
; ; ;
K=1,2,…..m 共m個類別;
其中是 Softmax-Loss 的中間步驟 Softmax 在 Forward Pass 的計算結果,k=1,…..,m,表示softmax的輸入埠編號。
求出之後,令,就求出了zk輸出埠應該呈現出來的值。是應該進行調整的數量。
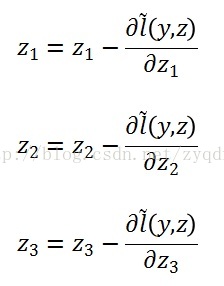
2. Softmax with loss 程式碼示例
clear all
clc
close all
x1=0;
x2=-0.4;
x3=0.2
for k=1:2160
v_k=k
p1=exp(x1);
p2=exp(x2);
p3=exp(x3);
np1=p1/(p1+p2+p3);
np2=p2/(p1+p2+p3);
np3=p3/(p1+p2+p3);
loss_1(k)=-log(np1);
loss_2(k)=-log(np2);
loss_3(k)=-log(np3);
x1=x1-(np1);
x2=x2-(np2-1); % the probability of x2 should be 1.
x3=x3-(np3);
end
figure
subplot(1,3,1)
plot(log(loss_1))
subplot(1,3,2)
plot(log(loss_2))
subplot(1,3,3)
plot(log(loss_3))
上述示例程式中,隨著x1,x2,x3值的更新,loss_2的值不斷減小。x2的概率值變數np2不斷增加,最終接近於1。Loss_2和loss_3的值不斷增加。x1和x3的概率值變數np1和np3不斷減小,最終接近於0。
圖1 x1,x2,x3的損失曲線圖 (f9)
3. 歐式距離損失函式示例程式碼
本例包含四組樣本,深度網路較好地擬合。網路引數為:
netsize=[inputsize,5,6,8,7,5,4];
(1) Main_function
clear all
clc
close all
TrainData =[1 2 3 4 5 6 7 8 9 10
1 9 17 25 33 41 49 57 65 73];
batchsize=4;
TrainData=TrainData(:,1:batchsize);
TrainLabel=[1 0.3 0.8 0.2;
1.8 0.8 1.2 1.1];
classnum=2;%輸出端數目
%獲取資料的維度
inputsize=size(TrainData ,1);
%獲取資料的數量
datanum=size(TrainData ,2);
% 用一個向量來定義網路的深度,以及每層神經元數目。
netsize=[inputsize,5,6,8,7,5,4];
% netsize=[inputsize,5,6,8,9,9,8,7,5,4];
%網路最後一層神經元數數目,再考慮一個偏置。
lastsize=netsize(end)+1;
%初始化網路引數,以結構體的形式儲存。
stack = initializeNet(netsize);
% 在訓練時,往往需要將引數轉成一列向量,提供給損失函式。
% stack ->stackTheta,netconfig儲存一些結構引數。
[stackTheta, netconfig] = stack2params(stack);
% 指定固定的最後一層的初始化的值;
rand('state',2)
lastTheta = 0.0005 * randn(lastsize * classnum, 1);
%最終網路需要的引數
Theta=[ lastTheta ; stackTheta ];
%lastTheta表示深度網路最後一層的權值
% the following part is for the traing epoch.
% batchsize=5;
%%每次訓練的小批量樣本數</span>
batchnum=floor(size(TrainData,2)/batchsize);
DataNum=size(TrainData,2);
alpha=1e-2;
%這是學習率,一般隨著網路的懸念都需要不斷的減小
lambda = 1e-4; % Weight decay parameter
for epoch=1:16000
v_epoch=epoch
if epoch>=16000
alpha=1e-3;
end
idx=randperm(DataNum);
for t=1:batchnum
subdata=TrainData(:,idx((t-1)*batchsize+1:(t)*batchsize));
sublabel=TrainLabel(:,idx((t-1)*batchsize+1:(t)*batchsize));
[cost(epoch),grad]=ReLUDNNCost(Theta,classnum,lastsize,netconfig,lambda,subdata,sublabel);
Theta=Theta-alpha*grad;
end
end
plot(log(cost))
(2) drelu
function dre= drelu(x)
dre=zeros(size(x));
dre(x>0)=1;
dre(x==0)=0.5; %這句可以不要
end
(3) relu
function re = relu(x)
re = max(x,0)-1;
end
(4) params2stack
function stack = params2stack(params, netconfig)
depth = numel(netconfig.layersizes);
stack = cell(depth,1);
prevLayerSize = netconfig.inputsize; % the size of the previous layer
curPos = double(1); % mark current position in parameter vector
for d = 1:depth
% Create layer d
stack{d} = struct;
% Extract weights
wlen = double(netconfig.layersizes{d} * prevLayerSize);
stack{d}.w = reshape(params(curPos:curPos+wlen-1), netconfig.layersizes{d}, prevLayerSize);
curPos = curPos+wlen;
% Extract bias
blen = double(netconfig.layersizes{d});
stack{d}.b = reshape(params(curPos:curPos+blen-1), netconfig.layersizes{d}, 1);
curPos = curPos+blen;
% Set previous layer size
prevLayerSize = netconfig.layersizes{d};
end
end
(5) ReLUDNNCost
function [cost,grad] = ReLUDNNCost(theta,numClasses,lasthiddenSize, netconfig,lambda, trainData,trainLabels)
%引數獲取的一些操作
lastTheta = reshape(theta(1:lasthiddenSize*numClasses), numClasses, lasthiddenSize);
%從theta向量中抽取網路權值引數並轉化
stack = params2stack(theta(lasthiddenSize*numClasses+1:end), netconfig);
stackgrad = cell(size(stack));
%這裡儲存在應用BP演算法求梯度時需要的資料
PARA=cell(numel(stack),1);
%傳進來的樣本數
datanum=size(trainData,2);
%開始前饋,網路雖然多層,但只是重複而已
data=trainData;
for d = 1:numel(stack)
PARA{d}.a=data;
z2=(stack{d}.w*data)+stack{d}.b*ones(1,datanum);
%ReLU函式
a2=relu(z2);
data=a2;
%ReLU函式的導函式
PARA{d}.daz=drelu(z2);
end
a2=[a2;ones(1,datanum)];
%開始求解損失
groundTruth=trainLabels;
v_groundTruth=groundTruth
M = lastTheta*a2;
v_M=M
% 損失函式,
cost=sum(sum((groundTruth-M).^2))./datanum;
%最後一層神經元的目標函式對lastTheta 的導數,
lastThetaGrad = -1/datanum*((groundTruth-M)*a2')+lambda*lastTheta;
% 輸出層誤差傳導至倒數第二層神經元的值
predelta=-lastTheta'*(groundTruth-M);
predelta=predelta(1:end-1,:);
for d = numel(stack):-1:1
delta=predelta.*PARA{d}.daz;
stackgrad{d}.w=delta*PARA{d}.a'/datanum;%.*PARA{d}.idx
stackgrad{d}.b=sum(delta,2)/datanum;
predelta=stack{d}.w'*delta;
end
grad = [lastThetaGrad(:) ; stack2params(stackgrad)];
end
(6) stack2params
function [params, netconfig] = stack2params(stack)
params = [];
for d = 1:numel(stack)
params = [params ; stack{d}.w(:) ;
stack{d}.b(:) ];
end
if nargout > 1
if numel(stack) == 0
netconfig.inputsize = 0;
netconfig.layersizes = {};
else
netconfig.inputsize = size(stack{1}.w, 2);
netconfig.layersizes = {};
for d = 1:numel(stack)
netconfig.layersizes = [netconfig.layersizes ; size(stack{d}.w,1)];
end
end
end
end
(7) initializeNet
function stack = initializeNet(netsize)
layersize=length(netsize(:));
stack = cell(layersize-1,1);
for l=1:layersize-1
hiddenSize=netsize(l+1);
visibleSize=netsize(l);
r =sqrt(6) / sqrt(hiddenSize+visibleSize+1);
rand('state',2)
stack{l}.w= rand(hiddenSize, visibleSize) * 2 * r - r; stack{l}.b= zeros(hiddenSize, 1);
end
end
(8) 執行結果
深度網路收斂,執行結果如下圖所示:
(f10)
輸出標籤值如下:
v_groundTruth =
0.2000 0.3000 1.0000 0.8000
1.1000 0.8000 1.8000 1.2000
深度網路實際擬合值如下:
v_M =
0.2001 0.3001 0.9999 0.7999
1.0999 0.8000 1.7999 1.2000
由上面資料比較可見,兩者差距較小,深度網路很好地擬合連續值輸出的樣本。
4. softmaxloss損失函式示例程式碼
將第3部分的程式碼進行修改,使得深度網路的損失函式採用softmaxwithloss損失函式。主要修改的部分為main_function.m 檔案和ReLUDNNCost.m檔案。本示例程式碼可以識別三個不同的種類。樣本數為5組樣本。
(1) Main_function
clear all; clc ; close all
TrainData =[1 2 3 4 5 6 7 8 9 10
1 9 17 25 33 41 49 57 65 73];
batchsize=5;
TrainData=TrainData(:,1:batchsize);
TrainLabel=[0 1 0 0 1;
1 0 0 1 0;
0 0 1 0 0];
classnum=3;%輸出端數目
%獲取資料的維度
inputsize=size(TrainData ,1);
%獲取資料的數量
datanum=size(TrainData ,2);
% 用一個向量來定義網路的深度,以及每層神經元數目。
netsize=[inputsize,5,6,8,7,5,4];
% netsize=[inputsize,5,6,8,9,9,8,7,5,4];
%網路最後一層神經元數數目,再考慮一個偏置。
lastsize=netsize(end)+1;
%初始化網路引數,以結構體的形式儲存。
stack = initializeNet(netsize);
% 在訓練時,往往需要將引數轉成一列向量,提供給損失函式。
% stack ->stackTheta,netconfig儲存一些結構引數。
[stackTheta, netconfig] = stack2params(stack);
% 指定固定的最後一層的初始化的值;
rand('state',2)
lastTheta = 0.0005 * randn(lastsize * classnum, 1);
%最終網路需要的引數
Theta=[ lastTheta ; stackTheta ];
%lastTheta表示深度網路最後一層的權值
% the following part is for the traing epoch.
% batchsize=5;
%%每次訓練的小批量樣本數</span>
batchnum=floor(size(TrainData,2)/batchsize);
DataNum=size(TrainData,2);
alpha=1e-2;
%這是學習率,一般隨著網路的懸念都需要不斷的減小
lambda = 1e-4; % Weight decay parameter
for epoch=1:3600
v_epoch=epoch
if epoch>=16000
alpha=1e-3;
end
idx=randperm(DataNum);
for t=1:batchnum
subdata=TrainData(:,idx((t-1)*batchsize+1:(t)*batchsize));
sublabel=TrainLabel(:,idx((t-1)*batchsize+1:(t)*batchsize));
[cost(epoch),grad]=ReLUDNNCost(Theta,classnum,lastsize,netconfig,lambda,subdata,
sublabel);
Theta=Theta-alpha*grad;
end
end
plot(log(cost))
(9) ReLUDNNCost
可識別三個種類的深度網路。
function [cost,grad] = ReLUDNNCost(theta,numClasses,lasthiddenSize, netconfig,lambda, trainData,trainLabels)
%引數獲取的一些操作
lastTheta = reshape(theta(1:lasthiddenSize*numClasses), numClasses, lasthiddenSize);
%從theta向量中抽取網路權值引數並轉化
stack = params2stack(theta(lasthiddenSize*numClasses+1:end), netconfig);
stackgrad = cell(size(stack));
%這裡儲存在應用BP演算法求梯度時需要的資料
PARA=cell(numel(stack),1);
%傳進來的樣本數
datanum=size(trainData,2);
%開始前饋,網路雖然多層,但只是重複而已
data=trainData;
for d = 1:numel(stack)
PARA{d}.a=data;
z2=(stack{d}.w*data)+stack{d}.b*ones(1,datanum);
%ReLU函式
a2=relu(z2);
data=a2;
%ReLU函式的導函式
PARA{d}.daz=drelu(z2);
end
a2=[a2;ones(1,datanum)];
%開始求解損失
groundTruth=trainLabels;
v_groundTruth=groundTruth
M = lastTheta*a2;
v_M=M;
p1=exp(M(1,:));
p2=exp(M(2,:));
p3=exp(M(3,:));
np1=p1./(p1+p2+p3)
np2=p2./(p1+p2+p3)
np3=p3./(p1+p2+p3)
dnp1=-(np1-trainLabels(1,:));
dnp2=-(np2-trainLabels(2,:));
dnp3=-(np3-trainLabels(3,:));
loss_1=log(np1);
loss_2=log(np2);
cost=(loss_1+loss_2)/2;
cost=0;
last_delta=[dnp1;dnp2;dnp3];
% 損失函式,
%最後一層神經元的目標函式對lastTheta 的導數,
% lastThetaGrad = -1/datanum*((groundTruth-M)*a2')+lambda*lastTheta;
lastThetaGrad = -1/datanum*(last_delta*a2')+lambda*lastTheta;
% 輸出層誤差傳導至倒數第二層神經元的值
predelta=-lastTheta'*last_delta;
predelta=predelta(1:end-1,:);
for d = numel(stack):-1:1
delta=predelta.*PARA{d}.daz;
stackgrad{d}.w=delta*PARA{d}.a'/datanum;%.*PARA{d}.idx
stackgrad{d}.b=sum(delta,2)/datanum;
predelta=stack{d}.w'*delta;
end
grad = [lastThetaGrad(:) ; stack2params(stackgrad)];
end
5. 總結
深度網路的資料預處理中,去均值是非常重要的步驟。而歸一化處理反而不是必須採用的步驟。
當深度神經網路可以對少量樣本進行很好的擬合,而對較多的樣本無法很好擬合的時候,很可能是深度網路的層數不夠深,即深度網路的特徵無法很好地表徵所有樣本的特徵。此時,可以通過加深網路的層次來使得深度網路對較多的樣本進行擬合。
需要記住的是:引數越多,模型越複雜,而越複雜的模型越容易過擬合。過擬合就是說模型在訓練資料上的效果遠遠好於在測試集上的效能。此時可以考慮正則化,通過設定正則項前面的hyper parameter,來權衡損失函式和正則項,減小引數規模,達到模型簡化的目的,從而使模型具有更好的泛化能力。
2.2 權重初始化
我們之前已經看過一個完整的神經網路,是怎麼樣通過神經元和連線搭建起來的,以及如何對資料做預處理。在訓練神經網路之前,我們還有一個任務要做,那就是初始化引數。
很小的隨機數,其實我們依舊希望初始的權重是較小的數,趨於0,但是就像我們剛剛討論過的一樣,不要真的是0。綜合上述想法,在實際場景中,我們通常會把初始權重設定為非常小的數字,然後正負儘量一半一半。這樣,初始的時候權重都是不一樣的很小隨機數,然後迭代過程中不會再出現迭代一致的情況。舉個例子,我們可能可以這樣初始化一個權重矩陣W=0.0001*np.random.randn(D,H)。這個初始化的過程,使得每個神經元的權重向量初始化為多維高斯中的隨機取樣向量,所以神經元的初始權重值指向空間中的隨機方向。
特別說明:其實不一定更小的初始值會比大值有更好的效果。還要具體問題具體分析。
方差歸一化,上面提到的建議有一個小問題,對於隨機初始化的神經元引數下的輸出,其分佈的方差隨著輸入的數量,會增長。我們實際上可以通過除以總輸入數目的平方根,歸一化每個神經元的輸出方差到1。也就是說,我們傾向於初始化神經元的權重向量為w = np.random.randn(n) / sqrt(n),其中n為輸入數。
2.3 正則化
在前一節裡我們說了我們要通過正則化來控制神經網路,使得它不那麼容易過擬合。有幾種正則化的型別供選擇:
L2正則化,我們在損失函式裡,加入對每個引數的懲罰度。也就是說,對於每個權重w,我們在損失函式里加入一項12λw2,其中λ是我們可調整的正則化強度。順便說一句,這裡在前面加上1/2的原因是,求導/梯度的時候,剛好變成λw而不是2λw。L2正則化理解起來也很簡單,它對於特別大的權重有很高的懲罰度,以求讓權重的分配均勻一些,而不是集中在某一小部分的維度上。我們再想想,加入L2正則化項,其實意味著,在梯度下降引數更新的時候,每個權重以W += -lambda*W的程度被拉向0。
L1正則化,這也是一種很常見的正則化形式。在L1正則化中,我們對於每個權重w的懲罰項為λ|w|。有時候,你甚至可以看到大神們混著L1和L2正則化用,也就是說加入懲罰項λ1∣w∣+λ2w2,L1正則化有其獨特的特性,它會讓模型訓練過程中,權重特徵向量逐漸地稀疏化,這意味著到最後,我們只留下了對結果影響最大的一部分權重,而其他不相關的輸入(例如『噪聲』)因為得不到權重被抑制。所以通常L2正則化後的特徵向量是一組很分散的小值,而L1正則化只留下影響較大的權重。在實際應用中,如果你不是特別要求只保留部分特徵,那麼L2正則化通常能得到比L1正則化更好的效果
最大範數約束,另外一種正則化叫做最大範數約束,它直接限制了一個上行的權重邊界,然後約束每個神經元上的權重都要滿足這個約束。實際應用中是這樣實現的,我們不新增任何的懲罰項,就按照正常的損失函式計算,只不過在得到每個神經元的權重向量w⃗ 之後約束它滿足∥w⃗∥2<c。在神經網路訓練學習率設定很高的時候,它也能很好地約束住權重更新變化,不至於直接掛掉。
Dropout:在訓練過程中,我們對每個神經元,都以概率p保持它是啟用狀態,1-p的概率直接關閉它。



