標籤（空格分隔）： 神經網路

0.回顧

cs231n （一）影象分類識別講了KNN cs231n （二）講了線性分類器：SVM和SoftMax cs231n （三）優化問題及方法 cs231n （四）反向傳播 cs231n （五）神經網路（part 1） 構建架構

1. 引言

五系列我們講了神經元模型，主要是加個啟用函式，然後定義損失，然後梯度下降。

2. 初始化資料和模型

這裡主要是資料預處理、權重初始化啦、還有損失函式的構建，優化問題不要著急哈。

1. 資料預處理階段

這個可是很重要的級階段，就像你做飯，食材是很重要的。 基本術語和符號：資料矩陣X = [NxD] = 100x3072

處理方式：

1. 減去均值，一般也稱作去中心化：想象一個數據云圖，就是把他們移到原點 實現程式碼： X -= np.mean(X, axis=0)，或者 X -= np.mean(X)

2. 歸一化資料， 將維度中心化，就是讓大家相差不太，數值近似相等 實現方法：

• 先對資料零中心化，然後除以標準差： X /= np.std(X, axis=0)
• 對每個維度都做歸一化，使得他們範圍一致【-1，1】，適用於：資料特徵的計算單位不一樣。

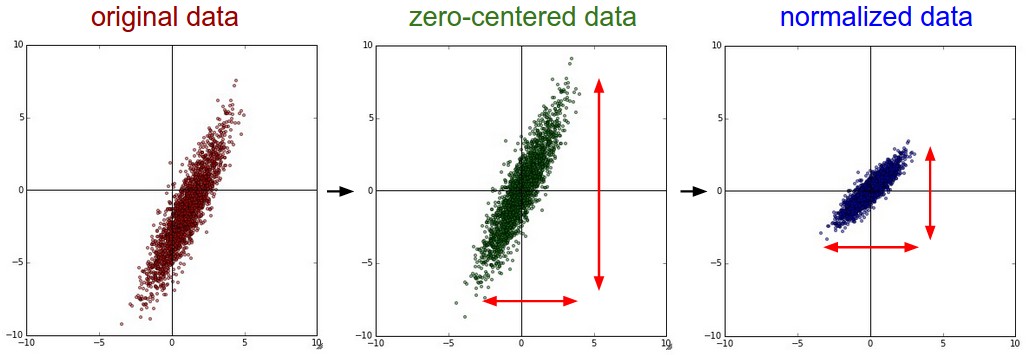
上述預處理方法可以從這裡看出：左 原始資料，中：減去均值方法，右：除以標準差之後的

白化和PCA

主要方法：先對資料零中心化，然後計算協方差矩陣。

# 輸入資料矩陣X = [N x D]
 

X -= np.mean(X, axis = 0) # 進行零中心化 重點
cov = np.dot(X.T, X) / X.shape[0] # 得到協方差矩陣

協方差矩陣是什麼？ 第（i,j）的元素就是第i個數據的j維度的協方差，矩陣的對角線上是元素的方差，我們可以對協方差矩陣進行SVD奇異值分解

U,S,V = np.linalg.svd(cov)

其中 U的列是特徵向量，S 是含有奇異值的1維陣列，為達到去除資料的相關性，我們把去零中心化的資料投影到特徵基上

Xrot = np.dot(X,U) # 去相關性

np.linalg.svd的返回值U中，特徵向量是按照特徵值的大小排列的，這樣就可以進行資料降維了俗稱

Xrot_reduced = np.dot(X, U[:,:100]) # Xrot_reduced 變成了 [N x 100]

這樣原始資料就降維到了 Nx100

接下來說一下白化，輸入：特徵基準上的資料，對每個維度除以其特徵值實現歸一化。

因為資料一般是符合高斯分佈的，白化後，那麼得到均值是零，協方差是相等的矩陣。

Xwhite = Xrot / np.sqrt(S + 1e-5)，這裡添加了1e-5是防止分母是零情況

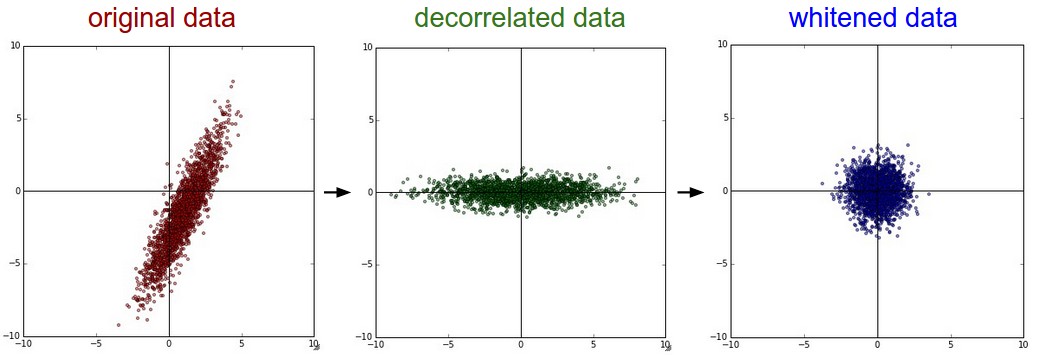
依次是：原始，PCA, 白化後的資料。

可以看看對於實際資料預處理之後的樣子。

左：原始資料，中：3072特徵值向量的最大的144，右：PCA降維後的資料，右右：白化資料

注意的是：我們一般是在訓練集上進行資料進行預處理，驗證和測試集減去的是訓練資料均值

2. 權重初始化

訓練前我們是沒有權重的怎麼辦？ 隨機啊 ！聰明！ 你簡直就是個天才，看看愛因斯坦怎麼說的吧

全零肯定不行

• 隨機數（比較小的） W = 0.01 * np.random.randn(D,H)， 想想嘛，數值太小，梯度又穿不透很深的網路，還有有一定問題滴,隨著輸入資料量的增長，隨機初始化的神經元的輸出資料的分佈中的方差也在增大

• 1/sqrt(n)校準方差 ：w = np.random.randn(n) / sqrt(n), n是輸入資料的數量,

• 稀疏初始化，權重矩陣設為零，神經元隨機連結，不好不好。

• 偏置初始化，一般是零， 至於其他的你可以多嘗試唄。

3.批歸一化

批量歸一化：在網路的每一層之前都做預處理，只不過是以另一種方式與網路整合在了一起

4. 正則化

上節內容已經說過了，就是用來防止過擬合的常見的有：

• L2正則化：就是二範數，就是$ \frac{1}{2}\lambda w^2$
• L1正則化：就是一範數，其實就是 $ \lambda_1|w|+\lambda_2w^2 $
• 最大正規化約束：加一個限制：$||\overrightarrow{w}||_2<c$ 就算學習率很大也不會出現數值爆炸。
• 隨機死亡：dropout： 來源於這裡

 
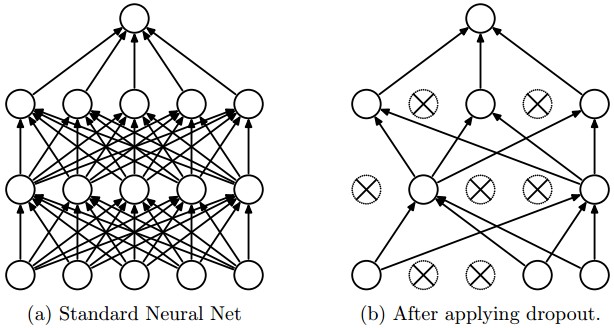
 """ Vanilla Dropout: Not recommended implementation (see notes below) """

p = 0.5 # probability of keeping a unit active. higher = less dropout

def train_step(X):
  """ X contains the data """
  
  # forward pass for example 3-layer neural network
  H1 = np.maximum(0, np.dot(W1, X) + b1)
  U1 = np.random.rand(*H1.shape) < p # first dropout mask
  H1 *= U1 # drop!
  H2 = np.maximum(0, np.dot(W2, H1) + b2)
  U2 = np.random.rand(*H2.shape) < p # second dropout mask
  H2 *= U2 # drop!
  out = np.dot(W3, H2) + b3
  
  # backward pass: compute gradients... (not shown)
  # perform parameter update... (not shown)
  
def predict(X):
  # ensembled forward pass
  H1 = np.maximum(0, np.dot(W1, X) + b1) * p # NOTE: scale the activations (要乘上p)
  H2 = np.maximum(0, np.dot(W2, H1) + b2) * p # NOTE: scale the activations
  out = np.dot(W3, H2) + b3
  

實際更多使用反向隨機失活（inverted dropout）

""" 
Inverted Dropout: Recommended implementation example.
We drop and scale at train time and don't do anything at test time.
"""

p = 0.5 # probability of keeping a unit active. higher = less dropout

def train_step(X):
  # forward pass for example 3-layer neural network
  H1 = np.maximum(0, np.dot(W1, X) + b1)
  U1 = (np.random.rand(*H1.shape) < p) / p # first dropout mask. Notice /p!
  H1 *= U1 # drop!
  H2 = np.maximum(0, np.dot(W2, H1) + b2)
  U2 = (np.random.rand(*H2.shape) < p) / p # second dropout mask. Notice /p!
  H2 *= U2 # drop!
  out = np.dot(W3, H2) + b3
  
  # backward pass: compute gradients... (not shown)
  # perform parameter update... (not shown)
  
def predict(X):
  # ensembled forward pass
  H1 = np.maximum(0, np.dot(W1, X) + b1) # no scaling necessary
  H2 = np.maximum(0, np.dot(W2, H1) + b2)
  out = np.dot(W3, H2) + b3

3. 損失函式

前面我們已經學過了 SVM and Softmax $\displaystyle L_i=\sum_{j\not=y_i}max(0,f_j-f_{y_i}+1)$ $\displaystyle L_i=-log(\frac{e^{f_{y_i}}}{\sum_je^{f_j}})$

標籤數目很大怎麼辦？ 使用softmax分層，

迴歸問題：預測實數的值的問題，預測房價，預測圖片東西的長度 對於這種問題，計算預測值和真實值之間的損失就夠了。 然後用L2平方正規化或L1正規化取相似度 $L_i=||f-y_i||^2_2$

4. 總結

直接看目錄不就知道了哇，哈哈。 預處理————正則化方法————損失函式