LeetCode基礎-圖-最小生成樹
阿新 • • 發佈:2019-02-18
加權圖:為每條邊關聯一個權值或者說成本的圖模型。
圖的生成樹:含有圖的所有頂點的無環連通子圖。
最小生成樹:加權無向圖的最小生成樹(MST)是它的一棵權值最小(所有邊的權值之和)的生成樹。
下圖是加權無向圖與它的最小生成樹。
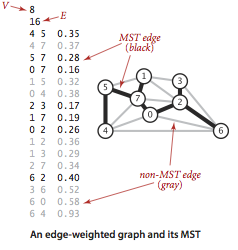
最小生成樹有兩個經典演算法:
- Prim 演算法
- Kruskal 演算法
如果一幅圖是非連通的,則只能用這個演算法計算所有連通分量的最小生成樹,合併在一起叫做最小生成森林。
還有幾點要注意的:
- 邊的權重未必是距離。
- 邊的權重可能小於等於 0 。
- 所有邊的權重都可能相同也可能不相同。
兩個性質:
- 用一條邊連線樹中的任意兩個頂點都會產生一個新的環。
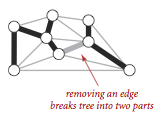
- 從樹中刪去一條邊可以得到兩棵獨立的樹。

圖的一種切分是把圖的所有頂點分為兩個 非空 且 不重複 的集合。橫切片是一條連線兩個屬於不同集合的邊。
通常,我們指定一個頂點集,然後隱式地認為它的補集是另一個頂點集。
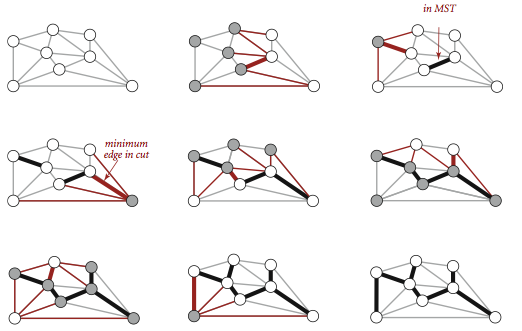
給定任意的切分,它的橫切邊中的權重最小者必然屬於圖的最小生成樹。
假設所有邊的權重不相同,則每幅連通圖都只有唯一的最小生成樹。
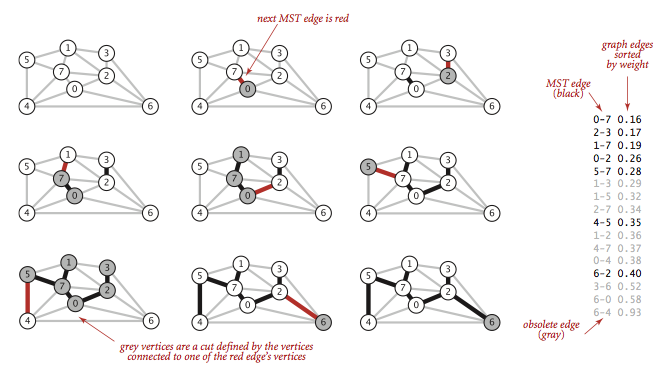
貪心演算法得到最小生成樹:
帶權重的邊的資料型別:
public class Edge implements Comparable<Edge>
{
private final int v; // one vertex
private 加權無向圖的資料型別:
“`
public class EdgeWeightedGraph
{
private final int V; // number of vertices
private int E; // number of edges
private Bag[] adj; // adjacency lists
public EdgeWeightedGraph(int V)
{
this.V = V;
this.E = 0;
adj = (Bag<Edge>[]) new Bag[V];
for (int v = 0; v < V; v++)
{
adj[v] = new Bag<Edge>();
}
}
public int V() { return V; }
public int E() { return E; }
public void addEdge(Edge e)
{
int v = e.either(), w = e.other(v);
adj[v].add(e);
adj[w].add(e);
E++;
}
public Iterable<Edge> adj(int v)
{ return adj[v]; }
public Iterable<Edge> edges()
{
Bag<Edge> list = new Bag<Edge>();
for (int v = 0; v < V; v++)
{
int selfLoops = 0;
foreach (Edge e in adj(v))
{
if (e.other(v) > v)
{
list.add(e);
}
// only add one copy of each self loop (self loops will be consecutive)
else if (e.other(v) == v)
{
if (selfLoops % 2 == 0) list.add(e);
selfLoops++;
}
}
}
return list;
}
}
Prim演算法
Prim演算法能夠得到任意加權無向圖的最小生成樹。
每一步都會為成長中的樹加一條邊。
Lazy實現:
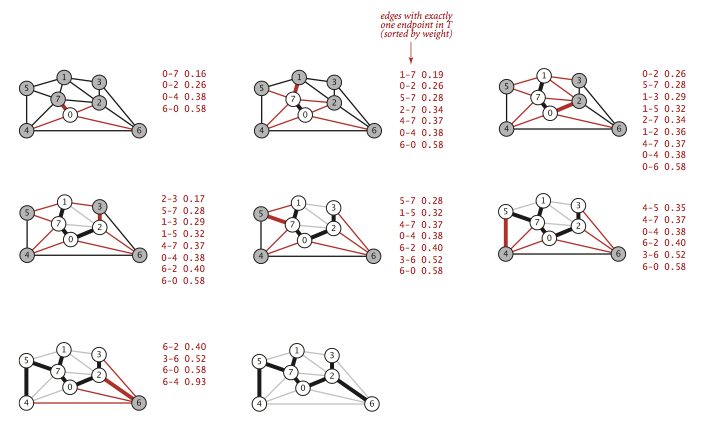
Eager實現:
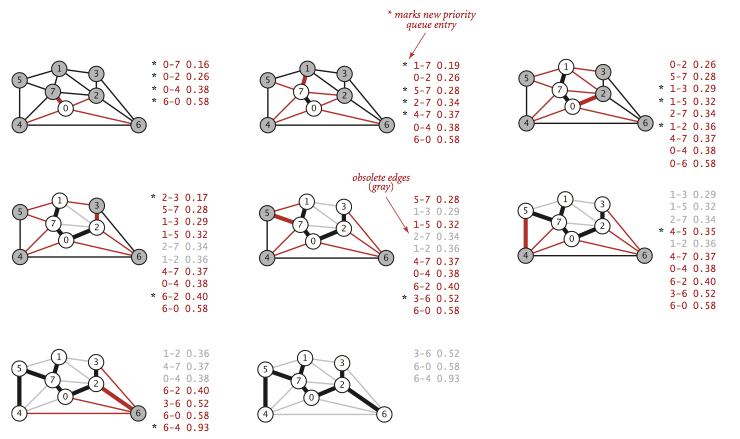
Kruskal 演算法
Kruskal 演算法的思想是按照邊的權重順序(從小到大)加入到樹中,加入的邊不會構成環。