2. 程式人生 > >【資料結構】二叉樹面試題總結

【資料結構】二叉樹面試題總結

阿新 • • 發佈：2019-02-18

為了對二叉樹的知識進行鞏固，今天我們來解析5道二叉樹的經典面試題。
這五道面試題如下：

  1. 求二叉樹中最遠兩個結點的距離；
  2. 判斷一棵樹是否是完全二叉樹；
  3. 由前序和中序遍歷序列重建二叉樹 （前序序列：1 2 3 4 5 6 - 中序序列:3 2 4 1 6 5）；
  4. 求二叉樹兩個結點的最近公共祖先；

  5. 將二叉搜尋樹轉化成有序的雙向連結串列；

    現在我們來對這五道題進行分析：

求二叉樹中最遠的兩個節點之間的距離

這道題如果沒有進行全面的分析，都以為只有一下一種情況：
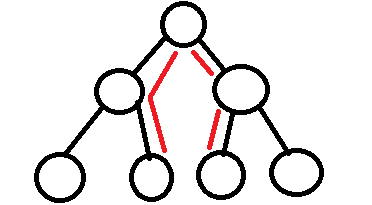
這裡寫圖片描述
這時，我們只需要分別求出左右子樹的高度然後相加再加1(根節點),就能得到最遠的兩個節點之間的距離了。
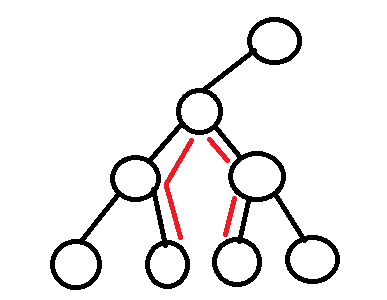
經過仔細分析，我們發現還有以下這種情況：
這裡寫圖片描述

時間負雜度為O（N*N）的解法

當二叉樹的根節點只有一顆子樹時，這時候二叉樹最遠節點的距離應該產生在子樹的左右子樹高度或這棵樹的高度再到根節點之間的距離兩者之間的，所以我們要求一顆樹最遠的兩個節點之間的距離，就需要求出這棵樹根節點的子樹的高度加上子樹根節點到這棵樹根節點的距離和子樹中最遠的兩個節點之間的距離，兩者的最大值就是這棵樹最遠的兩個節點之間的距離了。所以我們要求解一棵樹最遠的兩個節點之間的距離，就要去求子樹的高度和子樹的最遠的兩個節點之間的距離，直到我們求到子樹的根節點為NULL為止。

上面這種解法運用到了二叉樹先序遍歷的思想，先求根節點的最遠兩個節點之間的距離，再去求左子樹和右子樹最遠兩個節點之間的距離。下面我們來看一種時間複雜度為O(N)的解法

時間複雜度為O(N)的解法

這種解法就需要用到二叉樹後序遍歷的思想了，我們碰到樹的根節點先不去求當前根節點最遠的兩個節點之間的距離，轉而去求它左右子樹最遠的兩個節點之間的距離和左右子樹的高度，最後再來求當前根節點最遠的兩個節點之間的距離。
我們直接給出最優解法的程式碼:

//時間複雜度為O(N^2)的演算法
size_t DepthOfNode(BinaryTreeNode<int>* node)
{
    if (node == NULL)
    {
        return 0;
    }

    //分別求左右子樹
    size_t Left = DepthOfNode(node->
 
_Left) + 1;
    size_t Right = DepthOfNode(node->_Right) + 1;

    /*cout << "Left:"<<Left << endl;
    cout << "Right:" << Right << endl;*/
    return Left > Right ? Left : Right;
}

void _DisTanceOfNode(Node* root, size_t& LeftHigh, size_t RightHigh, size_t& Max);
size_t DisTanceOfNode(BinaryTree<int>& tree)
{
    size_t LeftHight = 0;
    size_t RightHight = 0;
    size_t Max = 0;

     _DisTanceOfNode(tree.ReturnRoot(), LeftHight, RightHight,Max);

     return Max;
}

時間複雜度為O(N*N)的演算法
void _DisTanceOfNode(Node* root, size_t& LeftHigh, size_t RightHigh,size_t& Max)
{
    if (root == NULL)
        return;

    if (root->_Left == NULL)
        LeftHigh = 0;

    if (root->_Right == NULL)
        RightHigh = 0;

    if (root->_Left != NULL)
        _DisTanceOfNode(root->_Left, LeftHigh, RightHigh, Max);

    if (root->_Right != NULL)
        _DisTanceOfNode(root->_Right, LeftHigh, RightHigh, Max);

    LeftHigh = DepthOfNode(root->_Left);
    RightHigh = DepthOfNode(root->_Right);

    //更新當前根節點的最遠兩個節點之間的距離
    if (LeftHigh + RightHigh + 1 > Max)
        Max = LeftHigh + RightHigh + 1;

}


void _DisTanceOfNode(Node* root, size_t& LeftHigh, size_t RightHigh, size_t& Max)
{
    if (root == NULL)
    {
        return;
    }
    _DisTanceOfNode(root->_Left, LeftHigh, RightHigh, Max);            //遞迴求左子樹最遠兩個節點之間的距離

    _DisTanceOfNode(root->_Right, LeftHigh,RightHigh, Max);                     //求右子樹

    LeftHigh = DepthOfNode(root->_Left);
    RightHigh = DepthOfNode(root->_Right);

    if (LeftHigh + RightHigh + 1 > Max)
        Max = LeftHigh + RightHigh + 1;
}
void Test1()
{
    int b[] = { 1, 2, 3, 5, '#', '#', '#', 4, '#', 6, '#', '#', '#' };
    int a[15] = { 1, 2, '#', 3, '#', '#', 4, 5, '#', 6, '#', 7, '#', '#', 8 };
    BinaryTree<int> t1(b, sizeof(b) / sizeof(b[0]), '#');
    t1.InOrder();
    t1.LevelOrder();
    cout << "樹中最遠的兩個節點之間的距離是？" << DisTanceOfNode(t1) << endl;
}

重建二叉樹

題目中給出了先序遍歷和中序遍歷，讓根據遍歷二叉樹的序列來對這顆二叉樹進行構建，要重建這顆二叉樹我們就得要要建立二叉樹的根節點，然後再分別構建這顆二叉樹的左右子樹，二叉樹的根節點元素就是前序序列的第一個元素，這樣我們根節點就能構建完成，接下來我們在中序遍歷中找到根節點元素，這個元素之前的序列就為左子樹的中序遍歷，之後的序列就為右子樹的中序遍歷，接下來我們去遞迴分別建立左右子樹就可以了

struct BinaryTreeNode
{
    int _value;
    BinaryTreeNode* _Left;
    BinaryTreeNode* _Right;

    BinaryTreeNode(const int& x)
        :_value(x)
        , _Left(NULL)
        , _Right(NULL)
    {}
};

typedef BinaryTreeNode Node;

Node* CreateBinaryTree(vector<int>& front, vector<int>& mid,int size)
{
    assert(front.size() == mid.size());

    if (size <= 0||front.size()==0||mid.size()==0)       //遞迴終止條件
        return NULL;

    //先建立根節點
    Node* root = new Node(front[0]);                    //前序遍歷的第一個節點為根節點的元素

    //在中序遍歷中找到根節點元素的所在位置
    int index = 0;
    for (index = 0; index < size; index++)
    {
        if (front[0] == mid[index])
            break;
    }

    if (index == size)
    {
        cout << "Invaid Input!!!建立失敗" << endl;
        exit(0);
    }

    //構建子序列
    vector<int> b;   //中序
    vector<int> a;   //先序遍歷
    for (int i = 0; i < index; i++)
    {
        b.push_back(mid[i]);
        a.push_back(front[i+1]);
    }

    //遞迴建立左子樹
    root->_Left = CreateBinaryTree(a, b, a.size());
    a.clear();
    b.clear();
    for (int i =index+1; i < size; i++)
    {
        b.push_back(mid[i]);
        a.push_back(front[i]);
    }

    //遞迴建立右子樹
    root->_Right = CreateBinaryTree(a, b, a.size());
    a.clear();
    b.clear();
    return root;
}

判斷一棵樹是否是完全二叉樹

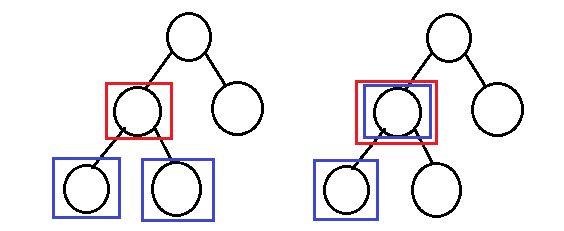
什麼是完全二叉樹呢？ 如下：
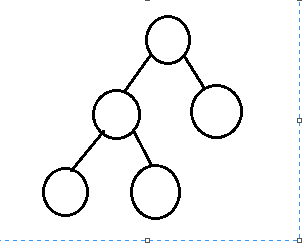
這裡寫圖片描述
若設二叉樹的深度為h，除第 h 層外，其它各層 (1～h-1) 的結點數都達到最大個數，第 h 層所有的結點都連續集中在最左邊，這就是完全二叉樹。
那麼我們怎麼判斷一棵樹是否是完全二叉樹呢，我們可以用一個佇列，通過層序遍歷的方式把二叉樹所有的節點都先入隊（包含空節點），當我們出隊的時候如果pop出來了空節點如果佇列中剩餘的所有節點都為NULL,那麼這棵樹就是完全二叉樹，如果佇列中還有非NULL節點，那麼這棵樹就不是完全二叉樹。

bool _LevelOrder(BinaryTreeNode<int>* root)
{
    queue<Node*> q;

    q.push(root);

    while ((q.front())!=NULL)
    {
        q.push(q.front()->_Left);
        q.push(q.front()->_Right);

        q.pop();
    }

    while (q.size() != 0)
    {
        if (q.front() == NULL)
            q.pop();

        else
            return false;
    }
    return true;
}

bool Is_Compelete(const BinaryTree<int>& t)
{
    if (t.ReturnRoot() == NULL)
        return true;                    //如果一棵樹為空樹，則這個樹可以看成完全二叉樹

    return _LevelOrder(t.ReturnRoot());
}

void Test3()
{
    //int a[15] = { 1, 2, '#', 3, '#', '#', 4, 5, '#', 6, '#', 7, '#', '#', 8 };
    int a[] = { 1, 2, 3, '#', '#', '#', '#', 5, '#', '#' };
    BinaryTree<int> t(a, sizeof(a) / sizeof(a[0]), '#');
    cout<<"是否是完全二叉樹:"<<Is_Compelete(t)<<endl;
}

求兩個節點的最近公共祖先

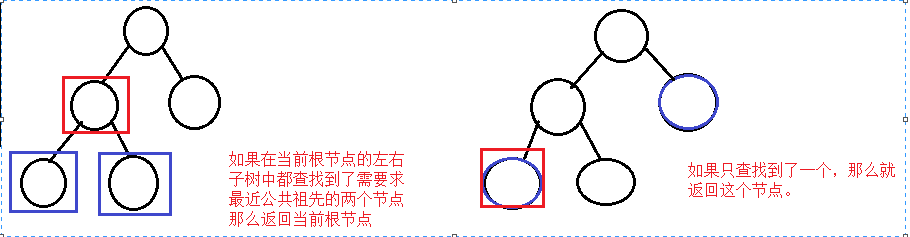
求二叉樹的任意兩個節點的最近公共祖先問題，包含以下兩種情況
1：這兩個節點都不是最近公共祖先。
2：這兩個節點有一個是公共祖先。
這裡寫圖片描述

方法一

我們可以藉助STL容器來實現這個問題，比方說一個順序表，我們從根節點開始，把從根節點到要查詢的節點之間的節點都pusn_back到vector中，這樣做等於說我們拿到了從根節點到需要求公共祖先的兩個節點的兩條路徑，我找到這兩條路徑中最後一個相等的節點，這個節點就是這兩個節點的最近公共祖先。

bool FindPath(BinaryTreeNode<int>* root, vector<int>& path,const int& value)
{
    /*尋找到達某一個節點的路勁找到了返回true並儲存路勁*/
    if (root == NULL)
    {
        return false;            //樹為NULL則路勁不存在
    }

    path.push_back(root->_Data); 
    if (root->_Data == value)
        return true;
    /*在左右子樹中查詢*/
    bool IfFind = FindPath(root->_Left, path, value) || FindPath(root->_Right, path, value);
    if (IfFind)
        return true;

    path.pop_back();               //如果在該節點下沒有找到就刪除路勁當中的節點
    return false;
}

Node* FindLCA(BinaryTree<int>& t,const int& n1,const int& n2)
{
    vector<int> Findn1Path;
    vector<int> Findn2Path;

    if (FindPath(t.ReturnRoot(), Findn1Path, n1) && FindPath(t.ReturnRoot(), Findn2Path, n2))
    {
        int index = -1;                      //記錄最後一個相等鍵值的位置
        int size = Findn1Path.size() > Findn2Path.size() ? Findn2Path.size() : Findn1Path.size();
        for (int i = 0; i < size; i++)
        {
            if (Findn1Path[i] != Findn2Path[i])
                break;                   //找到第一個不相等的鍵值
            index = i;
        }
        if (index == -1)
            return NULL;               //index=0  表示沒有相等的鍵值
        else
            return new Node(Findn1Path[index]);
    }

    cout << "兩個鍵值中有一個鍵值在二叉樹中沒有節點" << endl;
    return NULL;
}

void Test4()
{
    int a[15] = { 1, 2, '#', 3, '#', '#', 4, 5, '#', 6, '#', 7, '#', '#', 8 };
    BinaryTree<int> t(a, sizeof(a) / sizeof(a[0]), '#');
    cout<<FindLCA(t, 3, 5)->_Data<<endl;
    cout << FindLCA(t, 7, 8)->_Data << endl;
}

方法二：不需要容器的解法

這裡寫圖片描述

Node* _GetAncestor(Node* root, Node* node1, Node* node2)
{
    if (root == NULL)
        return NULL;

    Node* Left = _GetAncestor(root->_Left, node1, node2);
    Node* Right = _GetAncestor(root->_Right, node1, node2);

    if (Left&&Right)    //如果Left和Right都不為NULL   則root節點為他們的最近祖先
        return root;

    if (root == node2)
        return node2;
    if (root == node1)
        return node1;

    if ((Right == NULL) && Left)
        return Left;
    if ((Left == NULL) && Right)
        return Right;

    return NULL;
}

Node* GetAncestor(BinaryTree<int>& tree, Node* node1, Node* node2)
{
    //assert(node1);
    //assert(node2);
    Node* ancestor = _GetAncestor(tree.ReturnRoot(), node1, node2);
    return ancestor;
}



void Test2()
{
        int b[] = { 1, 2, 3, 5, '#', '#', '#', 4, '#', 6, '#', '#', '#' };
        int a[15] = { 1, 2, '#', 3, '#', '#', 4, 5, '#', 6, '#', 7, '#', '#', 8 };
        BinaryTree<int> t1(b, sizeof(b) / sizeof(b[0]), '#');
        t1.InOrder();
        t1.LevelOrder();
        cout << "最近的祖先是？" << GetAncestor(t1,t1.Find(5),t1.Find(7))->_Data<< endl;
}

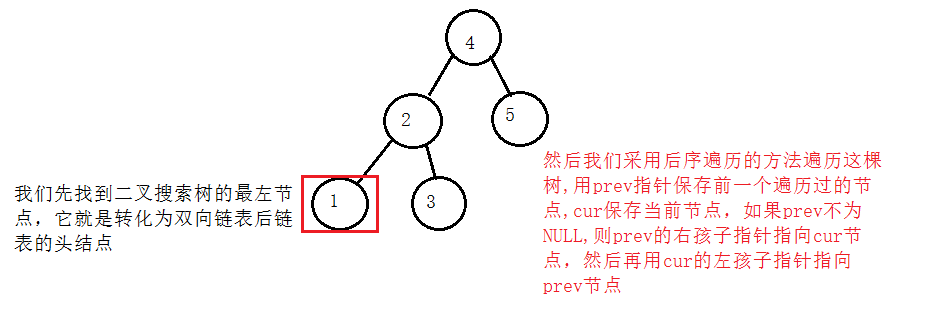
將一顆二叉搜尋樹轉化為雙向連結串列

這裡寫圖片描述

void _TreeToList(Node* cur, Node*& prev)
{
    if (cur == NULL)
        return;

    _TreeToList(cur->_left, prev);

    cur->_left = prev;
    if (prev != NULL)
        prev->_right = cur;

    prev = cur;
    _TreeToList(cur->_right, prev);
}

Node* TreeToList(BinarySearchTree<int>& tree)
{
    Node* Head = tree.ReturnRoot();
    while (Head->_left)
    {
        Head = Head->_left;         //二叉搜尋樹的最左節點就是單鏈表的第一個節點
    }          
    Node* Prev = NULL;
    Node* cur = tree.ReturnRoot();
    _TreeToList(cur, Prev);
    return Head;
}

void OrDerList(Node* root)
{
    assert(root);
    while (root)
    {
        cout << root->_key << " ";
        root = root->_right;
    }
    cout << endl;
}

void Test5()
{
    BinarySearchTree<int> t;
    t.Insert(5);
    t.Insert(4);
    t.Insert(7);
    t.Insert(3);
    t.Insert(6);
    t.Insert(9);
    t.Insert(2);
    t.Insert(0);
    t.Insert(1);
    t.Insert(8);
    t.InorderR();
    Node* head=TreeToList(t);
    OrDerList(head);
}

相關推薦

【資料結構】二叉樹面試題總結

為了對二叉樹的知識進行鞏固，今天我們來解析5道二叉樹的經典面試題。 這五道面試題如下： 求二叉樹中最遠兩個結點的距離； 判斷一棵樹是否是完全二叉樹； 由前序和中序遍歷序列重建二叉樹 （前序序列：1 2 3 4 5 6 - 中序序列:3 2 4 1 6

【資料結構】---------二叉樹面試題（具體的所有實現）

實現二叉樹的相關的操作： 先序遍歷樹（遞迴） 中序遍歷樹（遞迴） 後序遍歷樹（遞迴） 層序遍歷樹 建立一棵樹 樹的銷燬 樹的拷貝 二叉樹中節點的個數 二叉樹葉子節點的個數 二叉樹第K層節點的個數 樹的高度 在二叉樹中查詢節點 找當前節點的左子樹

【資料結構】二叉樹的相關操作（待更）

#include "stdio.h" #include "stdlib.h" typedef struct node { char data; struct node *rchild,*lchild; }bintnode; typedef bintnode *bintree;//指向該結構體

【資料結構】二叉樹的建立和遍歷（非遞迴）

該程式使用的是遞迴地建立方法，以及非遞迴的遍歷演算法 執行環境：Dev-C++ #include <stdio.h> #include <stdlib.h> typedef struct node{ char data; struct node *lchild

【資料結構】二叉樹的建立與遍歷（遞迴）

該程式全是使用遞迴的操作 執行環境是：Dev-C++ #include <stdio.h> #include <stdlib.h> typedef struct node{ char data; struct node *lchild,*rchild; }bi

【資料結構】二叉樹的應用

1、分別採用遞迴和非遞迴的方式編寫兩個函式，求一棵給定二叉樹中葉子節點的個數 2、返回一棵給定二叉樹在中序遍歷下的最後一個結點 3、假設二叉樹採用鏈式方式儲存，root為其根節點，p和q分別指向二叉樹中任意兩個結點，編寫一個函式，返回p和q最近的共同祖先。  #includ

【資料結構】二叉樹基本操作

文章目錄 BinaryTree.h BinaryTree.c Test.c 棧和佇列的相關函式: 棧：https://blog.csdn.net/weixin_41892460/article/details/82

【資料結構】二叉樹一些基本演算法

二叉樹中搜索某個元素的演算法。 /** * 查詢二叉樹中元素 * @param root * @param data * @return */ Boolean FinadIn

【資料結構】二叉樹介面的實現(用c語言實現）

二叉樹 概念 一棵二叉樹是結點的一個有限集合，該集合或者為空，或者是由一個根節點加上兩棵別稱為左子樹和右子樹的二又樹組成。 二叉樹的特點: 1.每個結點最多有兩棵子樹，即二叉樹不存在度大於2的結點。2.二又樹的子樹有左右之分，其子樹的次序不能顛倒   特殊的二

【資料結構】二叉樹的構建及遍歷（遞迴演算法）

題目描述： 編一個程式，讀入使用者輸入的一串先序遍歷字串，根據此字串建立一個二叉樹（以指標方式儲存）。 例如如下的先序遍歷字串： ABC##DE#G##F### 其中“#”表示的是空格，空格字元代表空樹。建立起此二叉樹以後，再對二叉樹進行中序遍歷，輸出遍歷結果。 具體程式

【資料結構】二叉樹的前中後遍歷與層次遍歷(遞迴與非遞迴)

水一波作業 #include <iostream> #include <cstring> //#pragma GCC optimize(2) #include<time.h> #include <map> #include &

【資料結構】二叉樹的遍歷及應用

前言       在二叉樹的應用中，常常要求在樹中查詢某些結點，或者對樹中的結點統一進行某種處理。因此，就提到了二叉樹的遍歷問題，對於線性結構來說，遍歷是一個很容易解決的問題，而二叉樹偏偏是一種非線性的結構，因此需要尋找一種規律。        二叉樹由三個基本單

【資料結構】二叉樹中任意兩節點的最近公共祖先節點

問題要求：任意給出二叉樹中的兩個節點，求他們的最近祖先 分三種情況： 1、該二叉樹是搜尋二叉樹 如果兩個節點的值都大於根節點，則遍歷右子樹查詢一個處於兩節點之間的值為最近祖先，如果兩個節點的值都小於根節點，則遍歷左子樹查詢一個兩節點之間的值為最近祖先 插入程式碼 Node*

【資料結構】二叉樹的實現

上篇部落格中，我們詳細說明了樹和二叉樹的資料結構及其特徵，本次，我們用C++來實現一下二叉樹 定義二叉樹節點結構 二叉樹需要定義指向左孩子和右孩子節點的指標，還有儲存的資料；我們在這把它的建構函式也寫出來 //定義一個二叉樹節點 template<typename

【資料結構】二叉樹的遍歷

二叉樹的遍歷大致可分為先序遍歷、中序遍歷、後序遍歷和層次遍歷四種。具體的實現原理都比較簡單，這裡不再描述，現在給出具體的遍歷演算法。本文給出了二叉樹遍歷的遞迴演算法和非遞迴演算法，這樣有助於對照了解。 二叉樹的結構體  typedef stru

【資料結構】二叉樹演算法題思路

首先需要做到掌握三種常規遍歷（前、中、後）以及按層遍歷，幾乎所有的演算法題都逃不開這三種方法。 其次，做二叉樹題目，很多情況都可以使用遞迴的方法來做，要經常想這個。 舉例： 1. 二叉樹映象問題 2. 二叉樹找子樹問題

【資料結構】二叉樹的順序儲存

原理 對於具有n個節點的完全二叉樹，如果按照從上至下和從左至右的順序對所有節點序號從0開始順序編號，則對於序號為 i(0<=i < n)的節點有： 1)如果i〉0，則序號為i節點的雙親節點的序號為(i-1)/2(/為整除)；如果i=0，則序

【資料結構】二叉樹（順序儲存、鏈式儲存）的JAVA程式碼實現

二叉樹是一種非線性的資料結構。它是由n個有限元素的集合，該集合或者為空、或者由一個稱為根(root)的元素及兩顆不相交的、被分別稱為左子樹、右子樹的二叉樹組成。當集合為空時，稱該二叉樹為空二叉樹。在二叉樹中，一個元素也可以稱做一個結點。二叉樹是有序的，即若將其左右兩個子樹顛倒

【資料結構】二叉樹的鏈式儲存結構（通過前序序列和中序序列構造二叉樹）

說明：需要分別輸入要二叉樹的前序序列和中序序列才能構建二叉樹。如果構建失敗，程式會報錯。 比如我們給定一個二叉樹，容易知道 前序序列為：GDAFEMHZ 中序序列為：ADEFGHMZ 程式執行結果： 原始碼 #include<stdio.h> #

【演算法與資料結構】二叉樹查詢

目錄 概要 樹的介紹 二叉樹的介紹 二叉查詢樹的C實現 1. 節點定義 2 遍歷 3. 查詢 4. 最大值和最小值 5. 前驅和後繼 6. 插入 7. 刪除 8. 列印 9. 銷燬二叉樹 完整的實現程式碼 二叉查詢樹的C測試程式 下面對