心血來潮 把這個基礎演算法結構補了

吶 先了解一下 可持久化線段樹 是什麼

自然是 可持久化 + 線段樹 啦 多用於詢問第m次修改後 某 節點 || 區間 的 值

線段樹自然是很好理解的(這個不知道就去補一下吧)

然而可持久化怎麼弄呢 總不能每次都copy整棵樹吧 不然時空複雜度都打得要死

因此 聰明的靈長類動物——裸猿人類們啊 發現

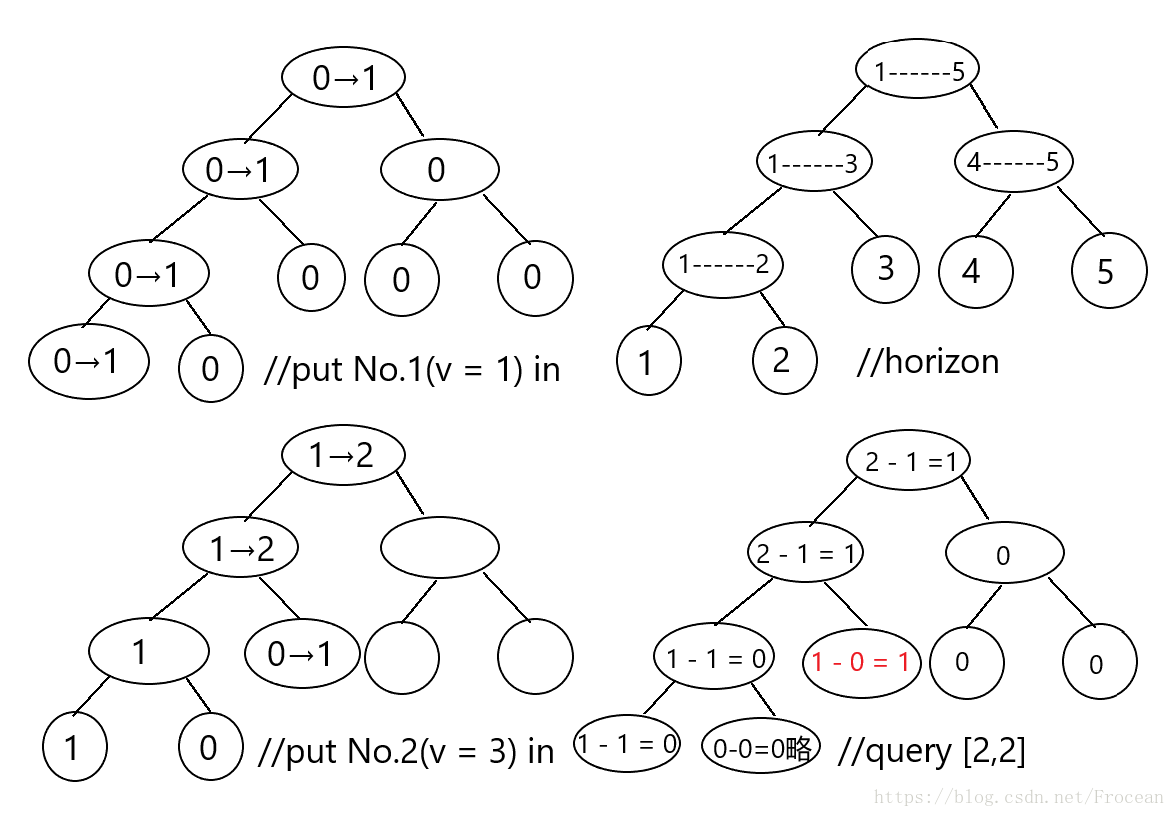
在修改一個 節點 || 區間 時啊 改變的只有他的祖先們

因此 我們只需要將該 節點 || 區間涉及的點 和 他們的祖先 複製一遍 賦上修改後該 節點 || 區間 的值 即可

首先是 單點修改(區間修改全靠自覺啦) 具體細節見程式碼 題目仍舊是洛谷的模板

Tip1:單點 修改 && 查詢 建樹只需將序列二分下去 區間記錄 左兒子 右兒子 節點上記錄 點權值

Tip2:儲存 節點 和 區間 的 陣列 大概開 樹上節點數的20倍(雖然本題我看有人開10倍 但我爆了 超凶的 =-=)

下面是程式碼加註釋 真的超詳細的=w=

#include <iostream>
#include <cstdio>
using namespace std;
const int MAX = 20000010;
struct Persistable_Segment_tree
{
	int ls,rs,v;//分別是該位置代表的節點或區間的左兒子右兒子和權值
} tr[MAX];
int edit[1 << 20] = {1},w[1 << 20],tot;//edit儲存節點版本 注意第一個(下標0)賦值為1表第一個版本 w儲存點初始權值
int build(int l,int r)
{//此處不能直接用++tot代替pos 因為跳轉到子程式中繼續搜尋下去 tot值會增加 而此處值代表當前節點編號 應不變
	int pos = ++tot;//tot是當前陣列末尾的位置 ++tot則是在末尾處新建儲存節點或區間的相關資訊 充分利用空間OwO真是太厲害了
	if (l == r)//區間左右相等 即只包括一個點 則只存點權
	{
		tr[pos].v = w[l];//記錄初始點權
		return pos;//pos是當前節點的編號 需返回 用以讓其父親節點記錄他
	}
	int mid = (l + r) >> 1;//二分存中點
	tr[pos].ls = build(l,mid);//記錄當前節點的左兒子編號
	tr[pos].rs = build(++mid,r);//記錄當前節點的右兒子編號
	return pos;//返回當前節點編號 需返回 用以讓其父親節點記錄他
}
int update(int ed,int l,int r,int p,int k)//在ed版本的基礎上 修改p點權值為k 記錄當前區間最左&&最右端的點l&&r 
{//此處不能直接++tot代替pos 因為跳轉到子程式中繼續搜尋下去 tot值會增加 而此處值代表當前節點編號 應不變
	int pos = ++tot;//記錄當前節點編號 充分利用空間OwO真是太奇妙了
	if (l == r)//當搜尋到單個節點了
	{
		tr[pos].v = k;//記錄修改後節點權值
		return pos;//返回當前節點編號 讓當前版本的父親記錄他
	}
	tr[pos].ls = tr[ed].ls;//將之前的該節點左兒子複製 (引用-->「把子節點指向前驅節點以備複用」)
	tr[pos].rs = tr[ed].rs;//將之前的該節點右兒子複製 因為之後只會改變兩兒子之一的值 這樣子可以確定該節點位置
	int mid = (l + r) >> 1;//二分存中點
	if (p <= mid) tr[pos].ls = update(tr[ed].ls,l,mid,p,k);//向下尋找 逼近p點 更改pos點的左兒子
	else tr[pos].rs = update(tr[ed].rs,++mid,r,p,k);//向下尋找 逼近p點 更改pos點的右兒子 用tr[ed]的原因是此時tr[pos]只有1深度的孩子的值
	return pos;//返回pos pos作為該點父親的某個兒子的位置 用以記錄
}
int found(int ed,int l,int r,int p)
{//ed是 某版本 儲存區間1~n的值 的位置
	if (l == r) return tr[ed].v;//找到該點 此時ed已經變為 記錄當前版本的p點的位置了 其v則是當前版本的p點的權值 返回
	int mid = (l + r) >> 1;
	if (p <= mid) return found(tr[ed].ls,l,mid,p);//向下尋找 逼近p點 ed變為ed的左兒子
	else return found(tr[ed].rs,++mid,r,p);//向下尋找 逼近p點 ed變為ed的右兒子
}
int main()
{
	int n,m,edition,mode,node,weight;//恪盡職守的變數定義
	scanf("%d%d",&n,&m);//發人深省的範圍輸入
	for (int a = 1 ; a <= n ; a ++) scanf("%d",&w[a]);//循規蹈矩的節點輸入
	build(1,n);//建樹 從區間 1 ~ n 開始遞迴 找左右兒子
	for (int a = 1 ; a <= m ; a ++)//循序漸進的命令處理
	{
		scanf("%d%d%d",&edition,&mode,&node);//五花八門的命令輸入
		if (mode % 2)//巧妙絕倫的判斷
		{
			scanf("%d",&weight);//撲朔迷離的補充輸入
			edit[a] = update(edit[edition],1,n,node,weight);//update解釋見子程式
		}//以update此時求出tr陣列的末尾 edit[a]意為在第a個版本時修改的點為edit[a-1]到edit[a]的點(上面那行程式讓本人想了很久很久)
		else//機智無比的轉折
		{
			edit[a] = edit[edition];//因為複製沒有建立新節點 因此當前版本的所有點等於當前版本(不是第a-1的版本)之前的所有點
			printf("%d\n",found(edit[edition],1,n,node));//輸出查詢某edition的某node的值
		}
	}
	return 0;//逢考必備的結尾
}
 

其實這行數似乎比線段樹的程式碼還少=-=這世道究竟......

好了接下來是 主席樹 不會講的太詳細哈 =-=

2018.9.8 經過一個多月偶爾的攻關 Frocean 還是決定向 STL 低下了頭 QAQ

2018.10.20 經過 Frocean 暗度陳倉的努力 最終還是趕跑了 大惡魔 STL

主席樹是用到了字首和的思想 =-=

然而一開始看網上各位 dalao 的解釋完全不懂 然後通過各種神奇的方式弄清了——

首先套用一下 “ 對於原序列的每一個字首 [ 1 ... i ] 建立出一棵線段樹維護值域上每個數出現的次數，則其樹是可減的 ”

什麼鬼東西 原序列哪裡有字首 不是輸入一個個權值嘛 而且每個字首建一棵樹 這是要爆炸

呵 (輕蔑) 事實上這個的意思是......我還是舉個例子吧

首先我們要把所有數的邊界弄出來做線段樹的邊界 (什麼線段樹啊 都沒說清楚) 別急 說好了舉例子的

例如我們一個數列 5 個數 互不相同 比如 233 19260817 6666 19491001 和 1000000007 五個數

最小最大是什麼? 好找到了我們拿他們做線段樹的邊界......等等這會死人的啊

於是離散一下 =-= 變成 1 3 2 4 和 5 到時候求答案轉換回去即可

好了線段樹怎麼造呢 看我強迫症畫了十五分鐘的圖 (畫圖太慢所以基本不畫OvO)

差不多了吧 =-= 意思很清楚

每次讀入一個數 然後包含他離散後數值的樹的區間 size 都加一 相當於單點修改

如果求區間 l 到 r 的 最小值 就用 第 r 次更新後樹的形態 減去 第 l - 1 (記住是 l - 1) 次更新的樹的形態

因此我們不能在空間只有 n 的 線段樹上做這事......之前不是有可持久化線段樹嘛

那我們對於每次更新到的點 像可持久化線段樹一樣 把加入第 i 個點當成第 i 個版本 然後同樣多加一堆節點就好了 然後就沒有然後了哈

話說網上那些圖都不畫單數個節點的真的是煩躁啊......

Tip1 : 初始離散化 + 去重 這裡用手打的但是沒去重 (手打去重我過不了QAQ)

Tip2 : 主席樹建樹先確定邊界 然後只用記每個點的左兒子和右兒子哈 權值到時候搜到第 k 大的時候返回點位置即可 (多個相同也不怕 看判斷方法)

Tip3 : 主席樹插入大概和上面的那樹差不多 於是關於 edit 和 ed 的 自覺上翻

Tip4 : 主席樹查詢很重要 細看哦 沒有細講主要是懶得畫圖......

洛谷的模板戳這裡 還有註釋'可能'在程式碼裡面哦 我對我的碼風莫名自信~

#include <algorithm>
#include <cstdio>
using namespace std;
const int MAXN = 200010;
int v[MAXN],bot[MAXN],newv[MAXN],edit[MAXN],tot;
//v存原點權 bot存點id (此處接sort處註釋) 
struct node {
    int l,r,siz; //l r 找位置 然後 siz 就是當前區間內的數的數量
} tr[MAXN << 5];
inline short cmp(int x,int y) {return v[x] < v[y];}
//通過比較v陣列大小讓bot當作排好序 
inline int r()
{
	char q = getchar(); int x = 0;
	while (q < '0' || q > '9') q = getchar();
	while ('0' <= q && q <= '9') x = (x << 3) + (x << 1) + q - (3 << 4),q = getchar();
	return x;
}
void insert(int ed,int l,int r,int i)
{ //同 可持久化線段樹 但是有點修改 不過原理一樣的
	++tr[ed].siz;
	if (l == r) return;
	int mid = (l + r) >> 1;
	if (i <= mid)
	{
		tr[++tot] = tr[tr[ed].l]; // 這種是l r siz一起更新的 省位置
		tr[ed].l = tot;
		insert(tr[ed].l,l,mid,i);
		return;
	}
	tr[++tot] = tr[tr[ed].r];
	tr[ed].r = tot;
	insert(tr[ed].r,++mid,r,i);
}
int out(int l,int r,int i,int j,int k)
{ // 查到點了返回點權 其實可以放在最外層..但我太懶了
	if (l == r) return v[bot[l]];
	int mid = (l + r) >> 1;
	int ex = tr[tr[j].l].siz - tr[tr[i].l].siz;
	//important ex是當前區間左兒子區間的size值 這裡用到了二叉查詢樹的思想
	if (ex >= k) return out(l,mid,tr[i].l,tr[j].l,k);
	return out(++mid,r,tr[i].r,tr[j].r,k - ex);
} //減去後是剩下要查的區間裡第k大的點數 之前是之前(相對的)全部區間裡第k大的點數
int main()
{
	int n = r(),m = r();
	for (int a = 1 ; a <= n ; ++ a) v[a] = r(),bot[a] = a;
	sort(bot + 1,bot + n + 1,cmp);
	for (int a = 1 ; a <= n ; ++ a) newv[bot[a]] = a;
	for (int a = 1 ; a <= n ; ++ a)
	{
		edit[a] = ++tot; //當前版本樹開頭接上上個節點的編號(+1) 
		tr[tot] = tr[edit[a - 1]]; //這個如果接版本 0 完全沒問題 
		insert(edit[a],1,n,newv[a]); //更新 確定子樹有範圍不怕 
	}
	while (m--)
	{
		int i = r(),j = r(),k = r();
		printf("%d\n",out(1,n,edit[i - 1],edit[j],k)); //處理詢問 
	}
	return 0;
}