CSDN−勿在浮沙築高臺
本文力求簡化SMO的演算法思想，畢竟自己理解有限，無奈還是要拿一堆公式推來推去，但是靜下心看完本篇並隨手推導，你會迎刃而解的。推薦參看SMO原文中的虛擬碼。

1.SMO概念

上一篇部落格已經詳細介紹了SVM原理，為了方便求解，把原始最優化問題轉化成了其對偶問題，因為對偶問題是一個凸二次規劃問題，這樣的凸二次規劃問題具有全域性最優解，如下：

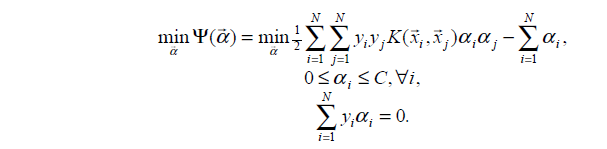
其中(xi,yi)表示訓練樣本資料，xi為樣本特徵,yi∈{−1,1}為樣本標籤，C為懲罰係數由自己設定。上述問題是要求解N個引數(α1,α2,α3,...,αN)，其他引數均為已知，有多種演算法可以對上述問題求解，但是演算法複雜度均很大。但1998年，由Platt提出的序列最小最優化演算法(SMO)可以高效的求解上述SVM問題，它把原始求解N個引數二次規劃問題分解成很多個子二次規劃問題分別求解，每個子問題只需要求解2個引數，方法類似於座標上升，節省時間成本和降低了記憶體需求。每次啟發式選擇兩個變數進行優化，不斷迴圈，直到達到函式最優值。

2.SMO原理分析

2.1視為一個二元函式

為了求解N個引數(α1,α2,α3,...,αN)，首先想到的是座標上升的思路，例如求解α1,可以固定其他N-1個引數，可以看成關於α1的一元函式求解，但是注意到上述問題的等式約束條件∑Ni=1yiαi=0,當固定其他引數時，引數α1也被固定，因此此種方法不可用。
SMO演算法選擇同時優化兩個引數，固定其他N-2個引數，假設選擇的變數為α1,α2,固定其他引數α3,α4,...,αN,由於引數α3,α4,...,αN的固定，可以簡化目標函式為只關於α1,α2的二元函式，Constant表示常數項(不包含變數α1,α2的項)。

minΨ(

α1,α2)=12K11α21+12K22α22+y1y2K12α1α2−(α1+α2)+y1v1α1+y2v2α2+Constant(1)其中vi=∑Nj=3αjyjK(xi,xj),i=1,2

2.2視為一元函式

由等式約束得：α1y1+α2y2=−∑Ni=3αiyi=ζ，可見ζ為定值。
等式α1y1+

相關推薦

【機器學習詳解】SMO演算法剖析

CSDN−勿在浮沙築高臺 本文力求簡化SMO的演算法思想，畢竟自己理解有限，無奈還是要拿一堆公式推來推去，但是靜下心看完本篇並隨手推導，你會迎刃而解的。推薦參看SMO原文中的虛擬碼。 1.SMO概念 上一篇部落格已經詳細介紹了SVM原理，為了方便求解，把原

【機器學習詳解】KNN分類的概念、誤差率及其問題

勿在浮沙築高臺 KNN概念         KNN(K-Nearest Neighbors algorithm)是一種非引數模型演算法。在訓練資料量為N的樣本點中，尋找最近鄰測試資料x的K個樣本，然

【機器學習詳解】解無約束優化問題：梯度下降、牛頓法、擬牛頓法

無約束優化問題是機器學習中最普遍、最簡單的優化問題。 x∗=minxf(x),x∈Rn 1.梯度下降 梯度下降是最簡單的迭代優化演算法，每一次迭代需求解一次梯度方向。函式的負梯度方向代表使函式值減小最快的方向。它的思想是沿著函式負梯度方向移動逐步逼

【機器學習詳解】線性迴歸、梯度下降、最小二乘的幾何和概率解釋

線性迴歸 即線性擬合，給定N個樣本資料（x1,y1）,(x2,y2)....(xN,yN)其中xi為輸入向量，yi表示目標值，即想要預測的值。採用曲線擬合方式，找到最佳的函式曲線來逼近原始資料。通過使得代價函式最小來決定函式引數值。 採用斯坦福大學公開課的

【機器學習筆記27】CART演算法-迴歸樹和分類樹

基本概念 分類和迴歸樹(classification and regression tree, CART) 是應用廣泛的決策樹學習方法，由特徵選擇、樹的生成和剪枝組成，既可以用做分類也可以用作迴歸。 迴歸樹 迴歸樹的定義 假設X和Y分別作為輸入和輸出變數，那麼

【機器學習基本理論】詳解最大似然估計（MLE）、最大後驗概率估計（MAP），以及貝葉斯公式的理解

總結 ora 二次 判斷 天都 特性 以及 解釋 意思 【機器學習基本理論】詳解最大似然估計（MLE）、最大後驗概率估計（MAP），以及貝葉斯公式的理解 https://mp.csdn.net/postedit/81664644 最大似然估計（Maximum lik

【機器學習筆記35】蟻群演算法

【參考資料】 【1】《蟻群演算法原理及其應用》 【2】測試資料: https://comopt.ifi.uni-heidelberg.de/software/TSPLIB95/tsp/att48.tsp.gz 演算法原理（以TSP問題為例） （1）引數初始化。令時間t=0和迴圈次數

【機器學習實戰之一】：C++實現K-近鄰演算法KNN

本文不對KNN演算法做過多的理論上的解釋，主要是針對問題，進行演算法的設計和程式碼的註解。 KNN演算法： 優點：精度高、對異常值不敏感、無資料輸入假定。 缺點：計算複雜度高、空間複雜度高。 適用資料範圍：數值型和標稱性。 工作原理：存在一個樣本資料集合，也稱作訓練樣本集，

【機器學習實戰系列】讀書筆記之AdaBoost演算法公式推導和例子講解（一）

最近在看整合演算法AdaBoost，推薦先看李航的統計學習方法第8章，然後再看機器學習實戰第7章，李航的書上的公式推導講的很詳細了，但是很多地方對於初學者來說，還是需要時間去理解和消化的。本文將從以下幾個方面來介紹AdaBoost演算法。一、AdaBoost演算法公式推導二、

【機器學習入門二】整合學習及AdaBoost演算法的python實現

本文主要基於周志華老師的《機器學習》第八章內容 個體與整合 整合學習通過構建並結合多個學習器來完成學習任務。整合學習的一般結構如圖所示： 先產生一組個體學習器，在用某種策略把它們結合在一起。個體學習器通常有一個現有的學習演算法從訓練資料產生，如決策

[機器學習]詳解分類演算法--決策樹演算法

前言 演算法的有趣之處在於解決問題,否則僅僅立足於理論,便毫無樂趣可言; 不過演算法的另一特點就是容易嚇唬人,又是公式又是圖示啥的,如果一個人數學理論知識過硬,靜下心來看,都是可以容易理解的,紙老虎一個,不過這裡的演算法主要指的應用型演算法

【機器學習實戰系列】讀書筆記之KNN演算法（三）

本次讀書筆記在於延續上一篇部落格的工程，做出微小的改動，即使用Matplotlib建立散點圖（散點圖使用DataMat矩陣的第一、第二列資料）。首先還是介紹一個相關知識點，方便程式碼瀏覽。知識點一：1、在使用Matplotlib生成圖表時，預設不支援漢字，所有漢字都會顯示成框

機器學習——詳解經典聚類演算法Kmeans

本文始發於個人公眾號：**TechFlow**，原創不易，求個關注 今天是機器學習專題的第12篇文章，我們一起來看下Kmeans聚類演算法。 在上一篇文章當中我們討論了KNN演算法，KNN演算法非常形象，通過距離公式找到最近的K個鄰居，通過鄰居的結果來推測當前的結果。今天我們要來看的演算法同樣非常直觀，

【機器學習基石筆記】一、綜述

model 但是 目標 學習 imp 選擇 處理 定義 條件 課程定位： 註重基礎、故事性 機器學習定義： data - Algo - improve 機器學習使用條件 1、有優化的目標，可量化的。 2、規則不容易寫下來，需要學習。 3、要有數據 一個可能的推薦

【機器學習基石筆記】二、感知機

證明 機器學習 sign 線性可分 缺點 學習 犯錯 nbsp 錯誤 感知機算法： 1、首先找到點，使得sign(wt * xt) != yt， 　　那麽如果yt = 1，說明wt和xt呈負角度，wt+1 = wt + xt能令wt偏向正角度。 　　如果yt = -1, 說

【機器學習基石筆記】三、不同類型的機器學習

質數 一個 非監督 輸入 編號 不同 象棋 按順序 pla 一、不同的output 1、二分類 2、多分類 3、回歸問題 4、structured learn: 從一個句子 -> 句子每個 詞的詞性。 　　輸出是一個結構化的東西。 　　例子：蛋白質數據 ->

【機器學習基石筆記】四、無法學習？

機器學習 估計 事情 永遠 pro app out 天下 oba 天下沒有白吃的午餐，從樣本內到樣本外永遠無法估計。 抽樣的話，樣本內頻率和樣本外概率相等PAC （probably approximately correct） 一個重要的事情是樣本要在總體分布中取。 E

【機器學習數學基礎】線性代數基礎

目錄 線性代數 一、基本知識 二、向量操作 三、矩陣運算 線性代數 一、基本知識 本書中所有的向量都是列向量的形式： \[\mathbf{\vec x}=(x_1,x_2,\cdots,x_n)^T=\begin{bmatrix}x_1\\x_2\

【動圖詳解】通過 User-Agent 識別爬蟲的原理、實踐與對應的繞過方法

開篇 隨著 Python 和大資料的火熱，大量的工程師蜂擁而上，爬蟲技術由於易學、效果顯著首當其衝的成為了大家追捧的物件，爬蟲的發展進入了高峰期，因此給伺服器帶來的壓力則是成倍的增加。企業或為了保證服務的正常運轉或為了降低壓力與成本，不得不使出各種各樣的技術手段來阻止爬蟲工程師們毫無節制的

【機器學習筆記02】最小二乘法（多元線性迴歸模型）

數學基礎 1.轉置矩陣 定義： 將矩陣A同序數的行換成列成為轉置矩陣ATA^TAT，舉例： A=(1203−11)A=\begin{pmatrix} 1 & 2 & 0 \\ 3 & -1 &