勿在浮沙築高臺

KNN概念  

      KNN(K-Nearest Neighbors algorithm)是一種非引數模型演算法。在訓練資料量為N的樣本點中，尋找最近鄰測試資料x的K個樣本，然後統計這K個樣本的分別輸入各個類別w_i下的數目k_i，選擇最大的k_i所屬的類別w_i作為測試資料x的返回值。當K=1時，稱為最近鄰演算法，即在樣本資料D中，尋找最近鄰x的樣本，把x歸為此樣本類別下。常用距離度量為歐式距離。

演算法流程：

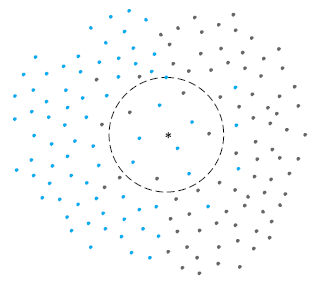
左圖所示：在二維平面上要預測中間'*'所屬顏色，採用K=11時的情況，其中有4黑色，7個藍色，即預測'*'為藍色。

右圖所示：當K=1時，即最近鄰演算法，相當於把空間劃分成N個區域，每個樣本確定一塊區域。每個區域中的點都歸屬於該樣本的類別，因為該區域的資料點與所用樣本相比與區域樣本最近，此演算法也被稱為Voronoi tessellation

--------------------------------------------------------------------------------------------------------------------------------------------

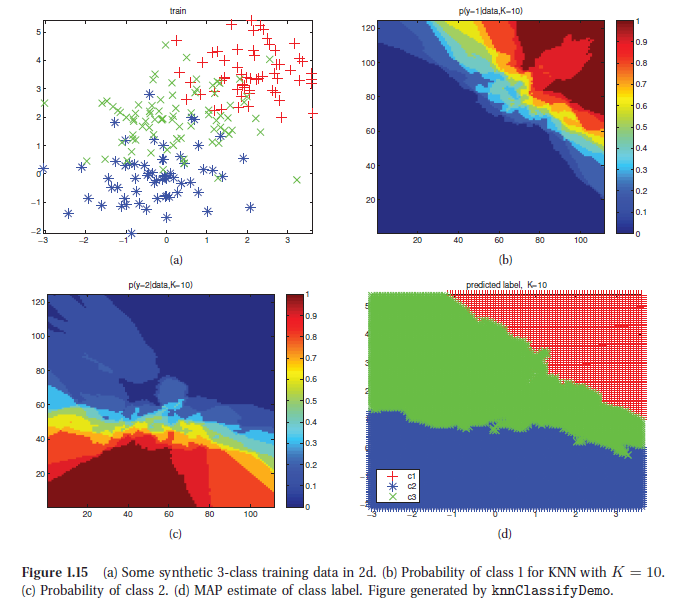
  下面四副影象是在一個二維平面上，資料點類別為3類，採用K=10。圖(a)為樣本資料點；圖(b)為平面上每個位置屬於y=1(對應‘+’)的概率熱量影象，圖(c)為類別y=2(對應'*')時對應的熱量影象；圖(d)採用MAP估計（即最大概率的類別）平面各點所屬類別。

------------------------------------------------------------------------------------------------------------------

KNN演算法誤差率

假設最優貝葉斯分類率記為P_B,根據相關論文證明KNN演算法的誤差率為：

當資料樣本量N趨於無窮大時，K=1時：    ，M為資料類別總數

當資料樣本量N趨於無窮大時，M=2時:;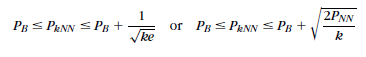

由公式看出，KNN的演算法要優於1-NN演算法，因為降低了誤差下界。並隨著k的增大，P_kNN漸近於最優誤差率P_B；事實上，當k->∞時(但仍然佔樣本總量N很小一部分)，KNN演算法準確率趨近於貝葉斯分類器。

KNN演算法的問題

• 當資料量N很大，同時資料維度D很高，搜尋效率會急劇下降。若採用暴力求解法，複雜度為。為增大效率，可以採用KD樹等演算法優化，見：KD樹與BBF演算法解析
• 有時根據現實情況，需要降低樣本數量，可以採用
  prototype editing或者condensing演算法等；prototype editing演算法採用自身資料樣本作為測試樣本，應用KNN演算法，若分類錯誤則剔除該樣本。
• 當樣本總量N很小時，會造成錯誤率上升。一種解決辦法是訓練度量距離方法，對不同的樣本採用不同的度量方法目的是為了降低錯誤率，此種方法可以分為：全域性方法(global)、類內方法(class-dependent)、區域性方法(locally-dependent)。

Ref：Machine Learning: A Probabilistic Perspective

         Pattern Recognition,4th.