codeforces-500【B思維】【C貪心】
New Year is coming in Line World! In this world, there are n cells numbered by integers from 1 to n, as a 1 × n board. People live in cells. However, it was hard to move between distinct cells, because of the difficulty of escaping the cell. People wanted to meet people who live in other cells.
So, user tncks0121 has made a transportation system to move between these cells, to celebrate the New Year. First, he thought of n
Currently, I am standing at cell 1
The first line contains two space-separated integers n (3 ≤ n ≤ 3 × 104) and t (2 ≤ t ≤ n) — the number of cells, and the index of the cell which I want to go to.
The second line contains n - 1 space-separated integers a1, a2, ..., an - 1 (1 ≤ ai ≤ n - i). It is guaranteed, that using the given transportation system, one cannot leave the Line World.
OutputIf I can go to cell t using the transportation system, print "YES". Otherwise, print "NO".
Examples input8 4 1 2 1 2 1 2 1output
YESinput
8 5 1 2 1 2 1 1 1output
NONote
In the first sample, the visited cells are: 1, 2, 4; so we can successfully visit the cell 4.
In the second sample, the possible cells to visit are: 1, 2, 4, 6, 7, 8; so we can't visit the cell 5, which we want to visit.
/* 搜尋
#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
const int MAXN=3*1e4+10;
int n,t;
int a[MAXN];
int mark[MAXN];
bool flag;
void find(int x)
{
if(mark[x]==t||x==t)
{
flag=1;
return ;
}
else if(mark[x]==-1) return ;
else find(mark[x]);
}
int main()
{
while(~scanf("%d %d",&n,&t))
{
memset(mark,-1,sizeof(mark));
for(int i=1;i<n;i++)
{
scanf("%d",&a[i]);
mark[i]=i+a[i];
}
flag=0;
if(mark[1]!=-1)
{
find(mark[1]);
}
if(flag) puts("YES");
else puts("NO");
}
return 0;
}*/
/* 標記:能到 i區域就能到 i + a[i]
#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
const int MAXN=3*1e4+10;
int n,t;
int a[MAXN];
bool vis[MAXN];
int main()
{
while(~scanf("%d %d",&n,&t))
{
memset(vis,0,sizeof(vis));
vis[1]=1;
for(int i=1;i<n;i++)
{
scanf("%d",&a[i]);
if(vis[i])
vis[i+a[i]]=1;
}
if(vis[t]) puts("YES");
else puts("NO");
}
return 0;
}*/
#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
const int MAXN=3*1e4+10;
int n,t;
int a[MAXN];
int main()
{
while(~scanf("%d %d",&n,&t))
{
for(int i=1;i<n;i++)
scanf("%d",&a[i]);
int cnt=1;
while(cnt<t)
{
cnt+=a[cnt];
}
if(cnt==t) puts("YES");
else puts("NO");
}
return 0;
}題目連結:點選開啟連結
B. New Year Permutation time limit per test 2 seconds memory limit per test 256 megabytes input standard input output standard output
User ainta has a permutation p1, p2, ..., pn. As the New Year is coming, he wants to make his permutation as pretty as possible.
Permutation a1, a2, ..., an is prettier than permutation b1, b2, ..., bn, if and only if there exists an integer k (1 ≤ k ≤ n) where a1 = b1, a2 = b2, ..., ak - 1 = bk - 1 and ak < bk all holds.
As known, permutation p is so sensitive that it could be only modified by swapping two distinct elements. But swapping two elements is harder than you think. Given an n × n binary matrix A, user ainta can swap the values of pi and pj (1 ≤ i, j ≤ n, i ≠ j) if and only if Ai, j = 1.
Given the permutation p and the matrix A, user ainta wants to know the prettiest permutation that he can obtain.
InputThe first line contains an integer n (1 ≤ n ≤ 300) — the size of the permutation p.
The second line contains n space-separated integers p1, p2, ..., pn — the permutation p that user ainta has. Each integer between 1and n occurs exactly once in the given permutation.
Next n lines describe the matrix A. The i-th line contains n characters '0' or '1' and describes the i-th row of A. The j-th character of thei-th line Ai, j is the element on the intersection of the i-th row and the j-th column of A. It is guaranteed that, for all integers i, j where 1 ≤ i < j ≤ n, Ai, j = Aj, i holds. Also, for all integers i where 1 ≤ i ≤ n, Ai, i = 0 holds.
OutputIn the first and only line, print n space-separated integers, describing the prettiest permutation that can be obtained.
Examples input7 5 2 4 3 6 7 1 0001001 0000000 0000010 1000001 0000000 0010000 1001000output
1 2 4 3 6 7 5input
5 4 2 1 5 3 00100 00011 10010 01101 01010output
1 2 3 4 5Note
In the first sample, the swap needed to obtain the prettiest permutation is: (p1, p7).
In the second sample, the swaps needed to obtain the prettiest permutation is (p1, p3), (p4, p5), (p3, p4).
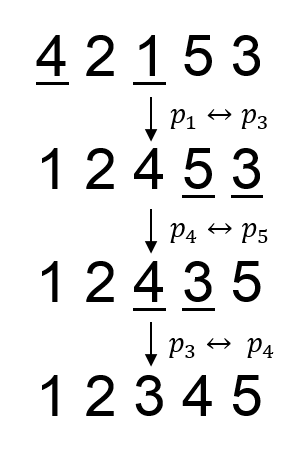
A permutation p is a sequence of integers p1, p2, ..., pn, consisting of n distinct positive integers, each of them doesn't exceed n. Thei-th element of the permutation p is denoted as pi. The size of the permutation p is denoted as n.
題意是根據矩陣判斷兩個元素之間能否進行直接交換,‘ 1 ’ 代表可以交換,‘ 0 ’ 代表不可以,要求輸出經過幾次交換後能得到的 “ 最完美的序列 ” ,‘‘ 最完美序列 ’’也就是儘量從小到大的排列的序列。
題解:值得注意的是這裡的元素直接不止能進行直接交換,還能進行間接交換,所以先用 floyd 預處理找到所有能夠交換(包括直接和間接)的元素,然後把能交換的元素進行冒泡就得到了“ 最完美序列 ”(因為其他的元素之間不能進行交換,只能按照原來的順序)。
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<iostream>
using namespace std;
int n,a[310];
char s[310][310];
bool vis[310][310];
int main()
{
while(~scanf("%d",&n))
{
for(int i=0;i<n;i++)
scanf("%d",&a[i]);
memset(vis,0,sizeof(vis));
for(int i=0;i<n;i++)
{
scanf("%s",s[i]);
for(int j=0;j<n;j++)
{
if(s[i][j]=='1')
vis[i][j]=1;
}
}
for(int k=0;k<n;k++)
{
for(int i=0;i<n;i++)
{
for(int j=0;j<n;j++)
{
if(vis[i][k]&&vis[k][j])
vis[i][j]=1;
}
}
}
for(int i=0;i<n;i++)
{
for(int j=i+1;j<n;j++)
{
if(vis[i][j]&&a[i]>a[j])
swap(a[i],a[j]);
}
}
for(int i=0;i<n;i++)
printf(i==0?"%d":" %d",a[i]);
puts("");
}
return 0;
}C. New Year Book Reading time limit per test 2 seconds memory limit per test 256 megabytes input standard input output standard output
New Year is coming, and Jaehyun decided to read many books during 2015, unlike this year. He has n books numbered by integers from 1 to n. The weight of the i-th (1 ≤ i ≤ n) book is wi.
As Jaehyun's house is not large enough to have a bookshelf, he keeps the n books by stacking them vertically. When he wants to read a certain book x, he follows the steps described below.
- He lifts all the books above book x.
- He pushes book x out of the stack.
- He puts down the lifted books without changing their order.
- After reading book x, he puts book x on the top of the stack.
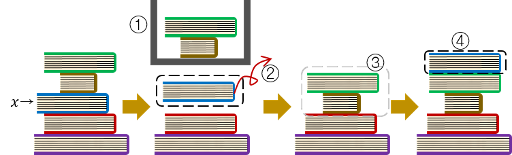
He decided to read books for m days. In the j-th (1 ≤ j ≤ m) day, he will read the book that is numbered with integer bj (1 ≤ bj ≤ n). To read the book, he has to use the process described in the paragraph above. It is possible that he decides to re-read the same book several times.
After making this plan, he realized that the total weight of books he should lift during m days would be too heavy. So, he decided to change the order of the stacked books before the New Year comes, and minimize the total weight. You may assume that books can be stacked in any possible order. Note that book that he is going to read on certain step isn't considered as lifted on that step. Can you help him?
InputThe first line contains two space-separated integers n (2 ≤ n ≤ 500) and m (1 ≤ m ≤ 1000) — the number of books, and the number of days for which Jaehyun would read books.
The second line contains n space-separated integers w1, w2, ..., wn (1 ≤ wi ≤ 100) — the weight of each book.
The third line contains m space separated integers b1, b2, ..., bm (1 ≤ bj ≤ n) — the order of books that he would read. Note that he can read the same book more than once.
OutputPrint the minimum total weight of books he should lift, which can be achieved by rearranging the order of stacked books.
Examples input3 5 1 2 3 1 3 2 3 1output
12Note
Here's a picture depicting the example. Each vertical column presents the stacked books.
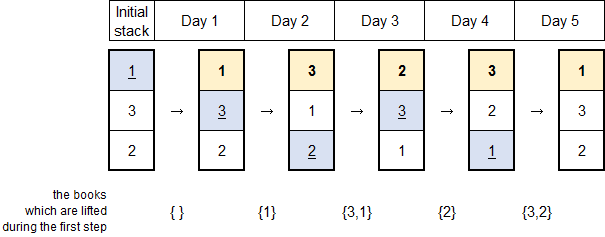
題意:一個人要讀n本書每本書有個重量 w [ i ],要讀 m 天,每天讀1本,他每天把要看的書抽出來(把上面的搬開,拿出要讀的書再把上面的書放回去),看完以後放到一摞書的最上面,問根據他的閱讀順序怎樣初始化書的排列順序能使他搬書的重量最小,求出這個最小重量
題解:先看一個序列1 1 1 1 1 1 1 2,對於這個序列,我們很明顯的策略是按1 2來排,因為看過以後放在最上面,所以每次讀1都不用搬書,對於一個閱讀序列的子序列a b,我們有兩種排法,按a b排代價是w[b],按b a排代價是w[a] + w[b],而且要明確的一點是確定了順序,代價也就隨之確定了,我們再將這個性質推廣到一般得出貪心結論:拿每本書第一次出現的順序作為初始序列,比如1 1 3 1 1 3 2 1 1 按此策略得到的初始序列為1 3 2,不管初始序列是什麼樣的,讀完 1 1 3以後的書的順序肯定都是確定的都為3 1 2,但是隻有初始序列為1 3 2時得到3 1 2的代價最小。由此可以得到結論:初始化書的最優排列順序就是:按照看書順序每一本第一次依次出現的順序。如樣例 1 3 2 3 1 ,那麼最優順序就是 1 3 2
/*
#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
int n,m;
int w[510],b[1010];
bool vis[1010];
int main()
{
while(~scanf("%d %d",&n,&m))
{
for(int i=1;i<=n;i++)
scanf("%d",&w[i]);
for(int i=1;i<=m;i++)
scanf("%d",&b[i]);
int ans=0;
for(int i=1;i<=m;i++)
{
memset(vis,0,sizeof(vis));
for(int j=i-1;j>=1;j--)
{
if(b[i]==b[j]) break; // 當找到相同時,已經拿完了放在 b[i]上面的書
if(!vis[b[j]]) // 已經拿過的書就不用再拿了
{
ans+=w[b[j]];
vis[b[j]]=1;
}
}
}
printf("%d\n",ans);
}
return 0;
}*/
// STL 實現
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<vector>
using namespace std;
int n,m;
int w[510],b[1010];
bool vis[1010];
vector<int> G;
int main()
{
while(~scanf("%d %d",&n,&m))
{
memset(vis,0,sizeof(vis));
G.clear();
for(int i=1;i<=n;i++)
scanf("%d",&w[i]);
for(int i=1;i<=m;i++)
{
scanf("%d",&b[i]);
if(!vis[b[i]])
{
G.push_back(b[i]);
vis[b[i]]=1;
}
}
int ans=0;
for(int i=1;i<=m;i++)
{
for(int j=0;j<G.size();j++)
{
if(b[i]==G[j])
{
G.erase(G.begin()+j);
G.insert(G.begin(),b[i]);
break;
}
else ans+=w[G[j]];
}
}
printf("%d\n",ans);
}
return 0;
}