漢諾塔問題

我最初接觸漢諾塔問題大概是在高三的時候，那個時候的數學試卷出了這麼一道題目，記得當初覺得這道題目很有趣，自己翻前覆後想了很多，但是終究還是沒有想出個所以然來，或許在那個時候，這道題目在老師和學霸的眼裡就是那麼簡單，不過對於那個時候的我來說，還是很有難度的一道題，當然今天不是，今天幾行程式碼就搞定了。

問題的描述

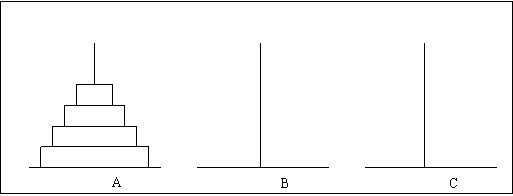
現在有三根連在一起的柱子，為了方便，我們標記他們為A，B，C。A柱子上從上到下按照金字塔狀疊放著n個不同大小的圓盤，現在我們想做這麼一件事情，我們要講A柱子上的圓盤全都移動的C柱子上去，但是我們有這麼一個限制：任何大的圓盤永遠都不能放置在小的圓盤上，現在我們要知道我們要怎麼移動圓盤，請程式設計寫出移動的軌跡。

思路

我們需要倒過來考慮這道問題。我們要怎麼辦呢？首先，第一個從A柱子移動倒C柱子的圓盤必然是A柱子的最後一個圓盤，然後A柱子的前n-1個圓盤必然都按照從上倒下的金字塔形狀疊在B柱子上。我們將A柱子的n個圓盤從A移動倒C之後，問題的規模就縮小了，問題變成了將B柱子上的n-1個圓盤藉助A移動倒C柱子上。依次類推。當問題的規模縮小倒1的時候，整個問題就已經解決了。

move(n, a, b, c)表示a柱子上有n個圓盤，要藉助b柱子從a柱子移動n個圓盤到c柱子，如果n == 1，我們直接輸出a-->c，表示將圓盤直接從a柱子移動倒c柱子，如果n > 1，我們這麼幹：先將前面的n - 1

一個例子

前面的思路其實就是遞迴了，我曾經不太敢相信遞迴，認為遞迴這東西有點玄乎，我怎麼確定最後這個程式一定會終止，我怎麼確定程式一定會對？遞迴的思想有點類似於管理，總經理管一堆經理，經理管一堆員工，員工管理一堆臨時工，有些事情總經理不需要親力親為，事實上他要是這麼幹就壞菜了，一個人怎麼頂起公司那麼多大大小小的事情，比如說總經理今年有一個目標，今年全年的業績要達到5千萬，總經理要做的就是給經理下命令，小李這個部門今年業績要達到1千萬，小花這個部門要達到500萬，等等。總經理只需要按照自己對部門的瞭解來下達自己的命令即可，他的估計裡或者說他相信自己給各個部門定下的目標一定回實現。

經理們也幹不了這麼多活，他們一樣的根據自己的預估來分派任務，每個員工應該搞定多少業績，他們確信自己定下的目標一定可以實現，然後這樣一層一層分派下去。

到了最底層的臨時工，他們分配的業績一定在他們能夠承受的範圍之內，也就是說雖然任務繁重，咬咬牙還是可以完成的，好了，他們一旦完成了任務，那麼相應的員工的任務完成了，經理的任務完成了，總經理的任務也完成了，這其實就是遞迴不是麼？

關於遞迴函式

從上面的例子，我們可以看到，從上到下，任務量是在減小的，也就是逐漸達到一個人可以接受的地步的，然後公司的層次也是有限的，沒有無限的分派任務下去，最後，其實大部分人乾的事情都是相同的，只有最底層的人乾的事情有所不同，這其實也反映了遞迴的三大條件，第一是一定要有遞迴出口，也就是要有下限，最後的小事一定要有人來辦，也就是說公司不能只有管理層，要有幹實事的人。第二就是向下派發的任務應該是逐漸減小的，如果沒有減小，說明你這個人沒幹什麼事，你的存在就沒有多麼大的意義了，第三，就是很多人乾的事情應該是一致的，這也是為什麼要遞迴的主要原因，乾的事不一樣就應該呼叫別的函數了，而不是函式本身了。

總結來說：相同的事是遞迴，然後不同的事就是遞迴出口了，然後問題的規模在逐漸減小。自己好好體會吧！

再談漢諾塔

我們反過頭來看這道題目，我們的任務是將n個圓盤從A柱子移動倒C柱子，總經理佈置任務了，小李，你將前n - 1個圓盤從A藉助C移動到B，然後寡人將第n個圓盤從A移動到C，最後小花，你將n - 1個圓盤從B藉助A移動到C，這件事情不就解決了嗎？寡人真是太聰明瞭。

然後經理們拿到自己分配的任務也開始琢磨了，他們發現領導還是很有水平的，因為自己的問題也可以按照領導的方法來解決啊，小李同志發現，自己先命令一個員工小豬，將n -2個圓盤從A藉助B倒C，然後自己將第n-1個圓盤從A移動到B，最後自己再命令小狗將n - 2個圓盤從C移動到B，這樣自己的問題不就解決了嗎？

就這樣一層一層下來，n最終會到1,然而這對於最底層的人來說非常簡單了，難道說A柱子上一個圓盤，要你藉助B到C還有困難嗎？這個人解決了問題，他就不會遞迴下去，遞迴就有了底線，他的完成會幫助他上面的人完成一部分工作，同樣的如果他上面的人完成了自己的工作，然後他的上面的上面的人也會完成一部分工作，一層一層上去，最終所有的任務都完成了。

小結

我並不是閒到蛋疼來寫一個很小很小的遞迴函式，只是自己曾經被這道題目傷害過，算是填補一下自己受傷過的心吧！

程式碼

程式碼其實用處不大，重要的是思想。我給出python的程式碼供參考：

#!/usr/bin/env python3
def move(n, a, b, c):
#n表示a中含有的盤子的數目，我們的目的是藉助盤子c將a中的盤子移動到b
#要求採用遞迴的演算法來解決這個問題
#引數n，表示3個柱子a、b、c中第1個柱子a的盤子數量，然後打印出把所有盤子從a藉助b移動到c的方法
    if n == 1:#遞迴終止條件
        print(a, '-->', c)
    else:
    #將a的前面的n-1個盤子藉助c移動到b
        move(n - 1, a, c, b)
    #將最後一個盤子從a移動到c
        move(1, a, b, c)
    #將n-1個圓盤從b藉助a移動c
        move(n - 1, b, a, c)
n = input('請輸入A柱子上的圓盤的數目:')
move(int(n), 'A', 'B', 'C')