弗洛伊德最短路演算法
暑假,小哼準備去一些城市旅遊。有些城市之間有公路,有些城市之間則沒有,如下圖。為了節省經費以及方便計劃旅程,小哼希望在出發之前知道任意兩個城市之前的最短路程。
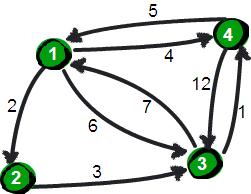
上圖中有4個城市8條公路,公路上的數字表示這條公路的長短。請注意這些公路是單向的。我們現在需要求任意兩個城市之間的最短路程,也就是求任意兩個點之間的最短路徑。這個問題這也被稱為“多源最短路徑”問題。
現在需要一個數據結構來儲存圖的資訊,我們仍然可以用一個4*4的矩陣(二維陣列e)來儲存。比如1號城市到2號城市的路程為2,則設e[1][2]的值為2。2號城市無法到達4號城市,則設定e[2][4]的值為∞。另外此處約定一個城市自己是到自己的也是0,例如e[1][1]為0,具體如下。
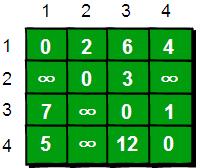
現在回到問題:如何求任意兩點之間最短路徑呢?通過之前的學習我們知道通過深度或廣度優先搜尋可以求出兩點之間的最短路徑。所以進行n2遍深度或廣度優先搜尋,即對每兩個點都進行一次深度或廣度優先搜尋,便可以求得任意兩點之間的最短路徑。可是還有沒有別的方法呢?
我們來想一想,根據我們以往的經驗,如果要讓任意兩點(例如從頂點a點到頂點b)之間的路程變短,只能引入第三個點(頂點k),並通過這個頂點k中轉即a->k->b,才可能縮短原來從頂點a點到頂點b的路程。那麼這個中轉的頂點k是1~n中的哪個點呢?甚至有時候不只通過一個點,而是經過兩個點或者更多點中轉會更短,即a->k1->k2b->或者a->k1->k2…->k->i…->b。比如上圖中從4號城市到3號城市(4->3)的路程e[4][3]原本是12。如果只通過1號城市中轉(4->1->3),路程將縮短為11(e[4][1]+e[1][3]=5+6=11)。其實1號城市到3號城市也可以通過2號城市中轉,使得1號到3號城市的路程縮短為5(e[1][2]+e[2][3]=2+3=5)。所以如果同時經過1號和2號兩個城市中轉的話,從4號城市到3號城市的路程會進一步縮短為10。通過這個的例子,我們發現每個頂點都有可能使得另外兩個頂點之間的路程變短。好,下面我們將這個問題一般化。
當任意兩點之間不允許經過第三個點時,這些城市之間最短路程就是初始路程,如下。

如現在只允許經過1號頂點,求任意兩點之間的最短路程,應該如何求呢?只需判斷e[i][1]+e[1][j]是否比e[i][j]要小即可。e[i][j]表示的是從i號頂點到j號頂點之間的路程。e[i][1]+e[1][j]表示的是從i號頂點先到1號頂點,再從1號頂點到j號頂點的路程之和。其中i是1~n迴圈,j也是1~n迴圈,程式碼實現如下。
- for(i=1;i<=n;i++)
- {
- for(j=1;j<=n;j++)
- {
- if ( e[i][j] > e[i][1]+e[1][j] )
- e[i][j] = e[i][1]+e[1][j];
- }
- }
在只允許經過1號頂點的情況下,任意兩點之間的最短路程更新為:
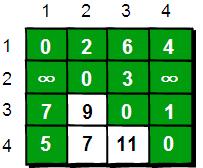
通過上圖我們發現:在只通過1號頂點中轉的情況下,3號頂點到2號頂點(e[3][2])、4號頂點到2號頂點(e[4][2])以及4號頂點到3號頂點(e[4][3])的路程都變短了。
接下來繼續求在只允許經過1和2號兩個頂點的情況下任意兩點之間的最短路程。如何做呢?我們需要在只允許經過1號頂點時任意兩點的最短路程的結果下,再判斷如果經過2號頂點是否可以使得i號頂點到j號頂點之間的路程變得更短。即判斷e[i][2]+e[2][j]是否比e[i][j]要小,程式碼實現為如下。
- //經過1號頂點
- for(i=1;i<=n;i++)
- for(j=1;j<=n;j++)
- if (e[i][j] > e[i][1]+e[1][j]) e[i][j]=e[i][1]+e[1][j];
- //經過2號頂點
- for(i=1;i<=n;i++)
- for(j=1;j<=n;j++)
- if (e[i][j] > e[i][2]+e[2][j]) e[i][j]=e[i][2]+e[2][j];
在只允許經過1和2號頂點的情況下,任意兩點之間的最短路程更新為:
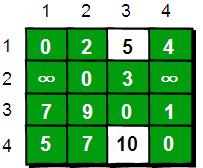
通過上圖得知,在相比只允許通過1號頂點進行中轉的情況下,這裡允許通過1和2號頂點進行中轉,使得e[1][3]和e[4][3]的路程變得更短了。
同理,繼續在只允許經過1、2和3號頂點進行中轉的情況下,求任意兩點之間的最短路程。任意兩點之間的最短路程更新為:
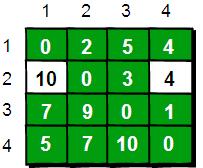
最後允許通過所有頂點作為中轉,任意兩點之間最終的最短路程為:
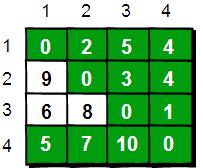
整個演算法過程雖然說起來很麻煩,但是程式碼實現卻非常簡單,核心程式碼只有五行:
- for(k=1;k<=n;k++)
- for(i=1;i<=n;i++)
- for(j=1;j<=n;j++)
- if(e[i][j]>e[i][k]+e[k][j])
- e[i][j]=e[i][k]+e[k][j];
這段程式碼的基本思想就是:最開始只允許經過1號頂點進行中轉,接下來只允許經過1和2號頂點進行中轉……允許經過1~n號所有頂點進行中轉,求任意兩點之間的最短路程。用一句話概括就是:從i號頂點到j號頂點只經過前k號點的最短路程。其實這是一種“動態規劃”的思想,關於這個思想我們將在《啊哈!演算法2——偉大思維閃耀時》在做詳細的討論。下面給出這個演算法的完整程式碼:
- #include <stdio.h>
- int main()
- {
- int e[10][10],k,i,j,n,m,t1,t2,t3;
- int inf=99999999; //用inf(infinity的縮寫)儲存一個我們認為的正無窮值
- //讀入n和m,n表示頂點個數,m表示邊的條數
- scanf("%d %d",&n,&m);
- //初始化
- for(i=1;i<=n;i++)
- for(j=1;j<=n;j++)
- if(i==j) e[i][j]=0;
- else e[i][j]=inf;
- //讀入邊
- for(i=1;i<=m;i++)
- {
- scanf("%d %d %d",&t1,&t2,&t3);
- e[t1][t2]=t3;
- }
- //Floyd-Warshall演算法核心語句
- for(k=1;k<=n;k++)
- for(i=1;i<=n;i++)
- for(j=1;j<=n;j++)
- if(e[i][j]>e[i][k]+e[k][j] )
- e[i][j]=e[i][k]+e[k][j];
- //輸出最終的結果
- for(i=1;i<=n;i++)
- {
- for(j=1;j<=n;j++)
- {
- printf("%10d",e[i][j]);
- }
- printf("\n");
- }
- return0;
- }
有一點需要注意的是:如何表示正無窮。我們通常將正無窮定義為99999999,因為這樣即使兩個正無窮相加,其和仍然不超過int型別的範圍(C語言int型別可以儲存的最大正整數是2147483647)。在實際應用中最好估計一下最短路徑的上限,只需要設定比它大一點既可以。例如有100條邊,每條邊不超過100的話,只需將正無窮設定為10001即可。如果你認為正無窮和其它值相加得到一個大於正無窮的數是不被允許的話,我們只需在比較的時候加兩個判斷條件就可以了,請注意下面程式碼中帶有下劃線的語句。
- //Floyd-Warshall演算法核心語句
- for(k=1;k<=n;k++)
- for(i=1;i<=n;i++)
- for(j=1;j<=n;j++)
- if(e[i][k]<inf && e[k][j]<inf && e[i][j]>e[i][k]+e[k][j])
- e[i][j]=e[i][k]+e[k][j];
上面程式碼的輸入資料樣式為:
- 48
- 122
- 136
- 144
- 233
- 317
- 341
- 415
- 4312
第一行兩個數為n和m,n表示頂點個數,m表示邊的條數。
接下來m行,每一行有三個數t1、t2 和t3,表示頂點t1到頂點t2的路程是t3。
得到最終結果如下:
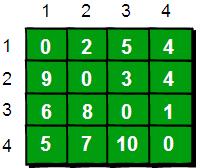
通過這種方法我們可以求出任意兩個點之間最短路徑。它的時間複雜度是O(N3)。令人很震撼的是它竟然只有五行程式碼,實現起來非常容易。正是因為它實現起來非常容易,如果時間複雜度要求不高,使用Floyd-Warshall來求指定兩點之間的最短路或者指定一個點到其餘各個頂點的最短路徑也是可行的。當然也有更快的演算法,請看下一節:Dijkstra演算法。
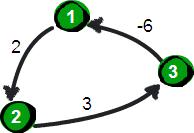
另外需要注意的是:Floyd-Warshall演算法不能解決帶有“負權迴路”(或者叫“負權環”)的圖,因為帶有“負權迴路”的圖沒有最短路。例如下面這個圖就不存在1號頂點到3號頂點的最短路徑。因為1->2->3->1->2->3->…->1->2->3這樣路徑中,每繞一次1->-2>3這樣的環,最短路就會減少1,永遠找不到最短路。其實如果一個圖中帶有“負權迴路”那麼這個圖則沒有最短路。
此演算法由Robert W. Floyd(羅伯特·弗洛伊德)於1962年發表在“Communications of the ACM”上。同年Stephen Warshall(史蒂芬·沃舍爾)也獨立發表了這個演算法。Robert W.Floyd這個牛人是朵奇葩,他原本在芝加哥大學讀的文學,但是因為當時美國經濟不太景氣,找工作比較困難,無奈之下到西屋電氣公司當了一名計算機操作員,在IBM650機房值夜班,並由此開始了他的計算機生涯。此外他還和J.W.J. Williams(威廉姆斯)於1964年共同發明了著名的堆排序演算法HEAPSORT。堆排序演算法我們將在第七章學習。Robert W.Floyd在1987年獲得了圖靈獎。
