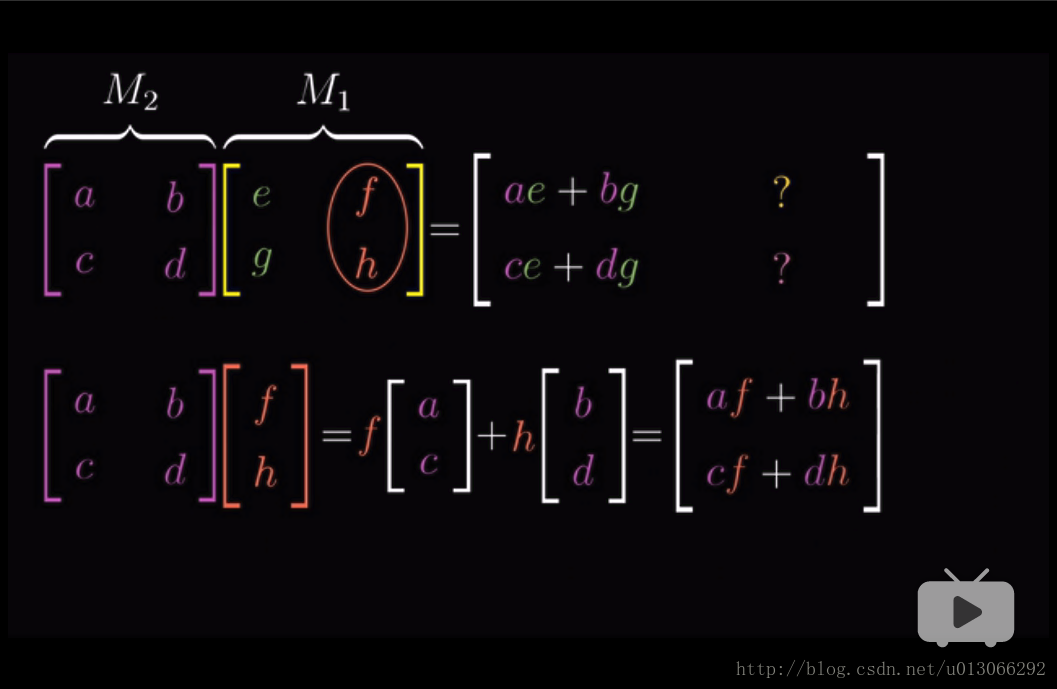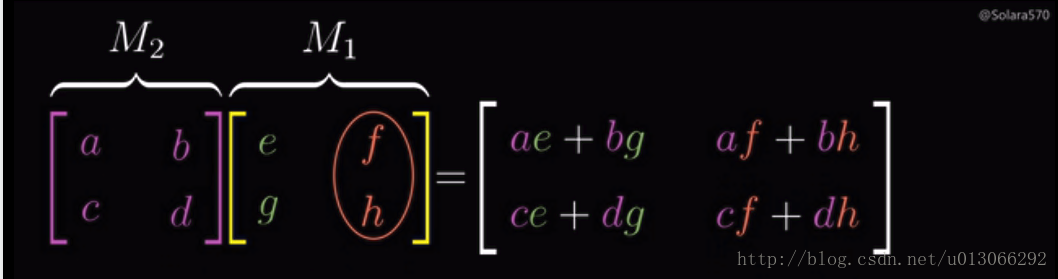線性代數的本質(筆記一)
寫在前面
本課程主要通過幾何來了解線性代數
1. 向量
對於向量有三種觀點:
- 物理學
具有大小和方向 - 計算機
陣列,列表 - 數學
概括前面兩者,只要保證向量的加法和數乘有意義即可。
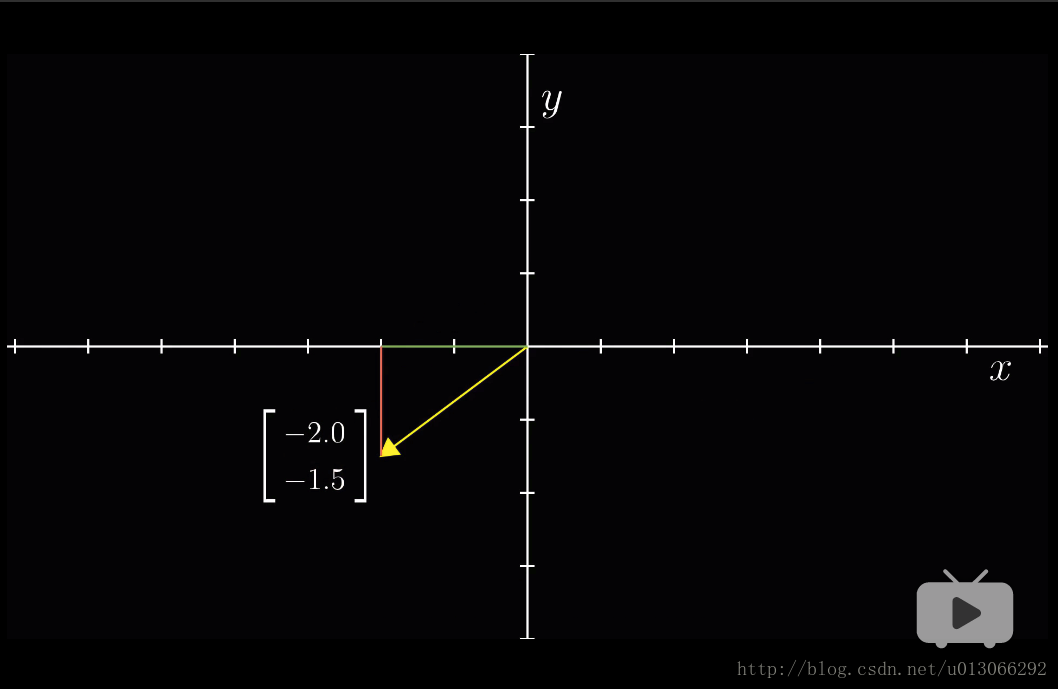
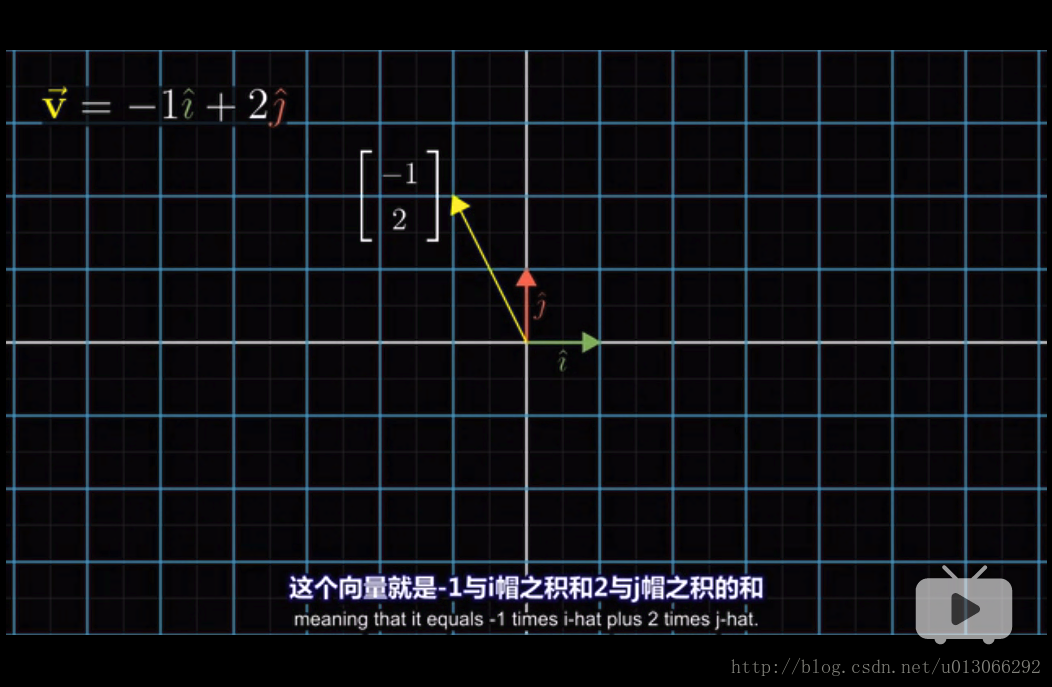
本課程由於是通過幾何來了解,所以會通過座標軸來表現向量,需要想象向量是空間中的箭頭, 進一步就是向量是有序的數列 。
線性代數即圍繞向量的加法和數乘展開。
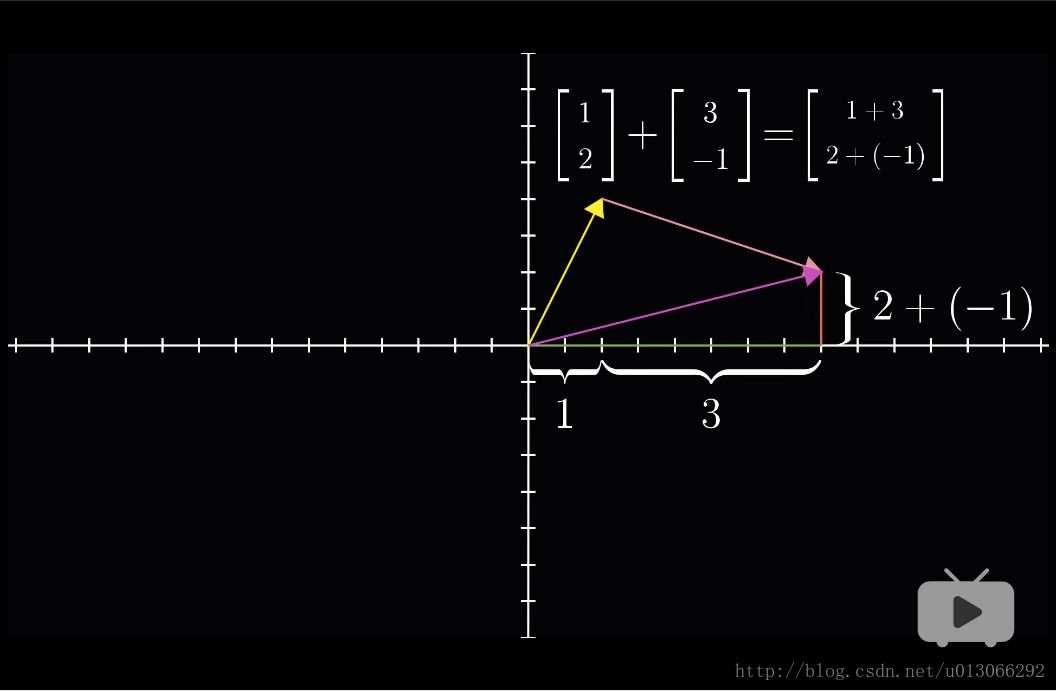
1.1 加法
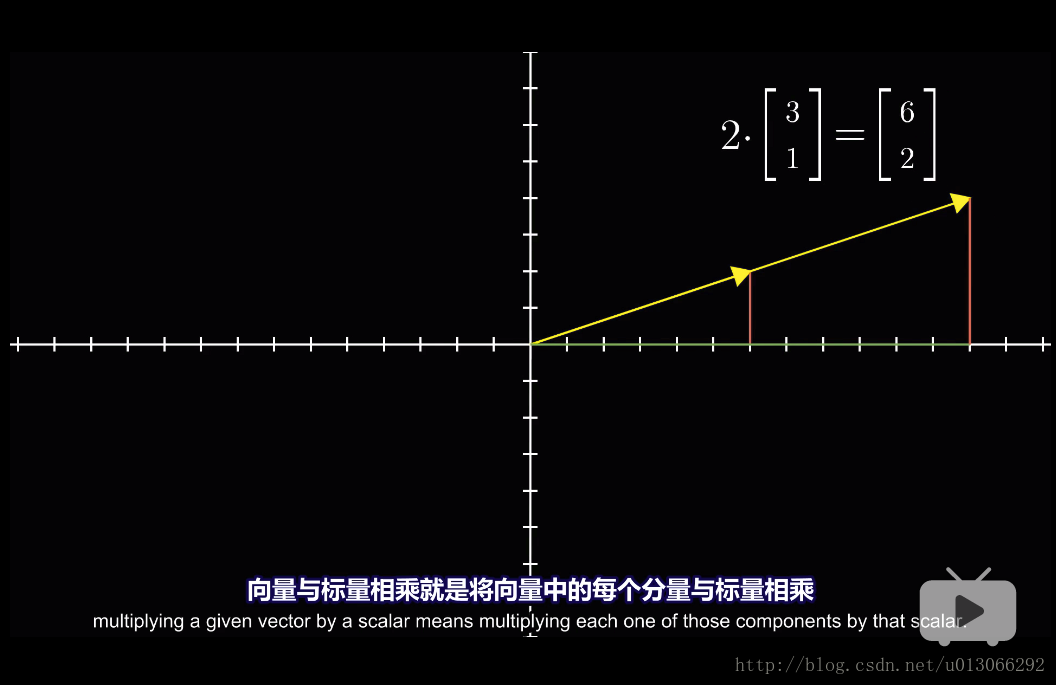
1.2 數乘
2.線性組合、張成的空間和基
2.1 基向量
在一個座標系裡,不用侷限於這種x軸和y軸的基向量,也可以選擇不同方向的基向量 ,但也意味著在相同座標裡,它們所表現出來的向量是不等價的。
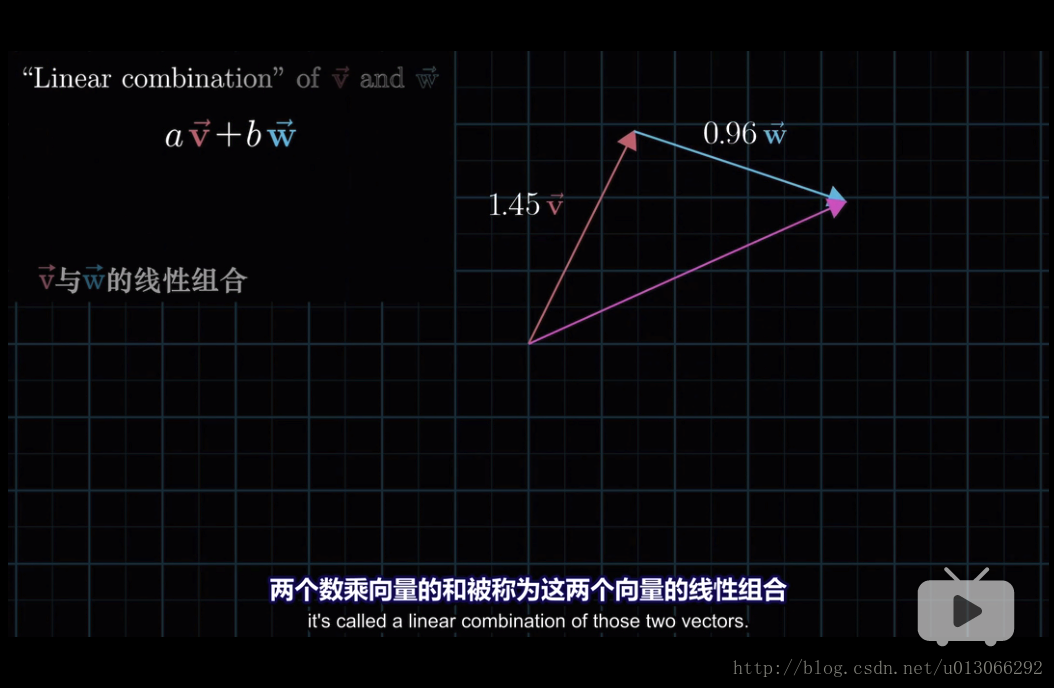
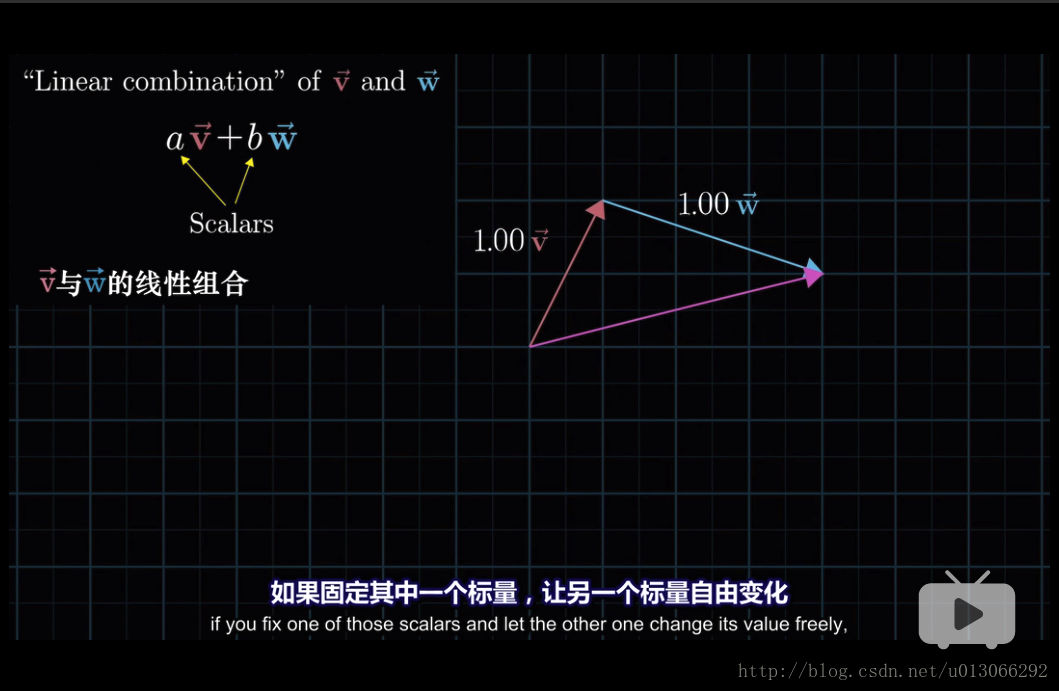
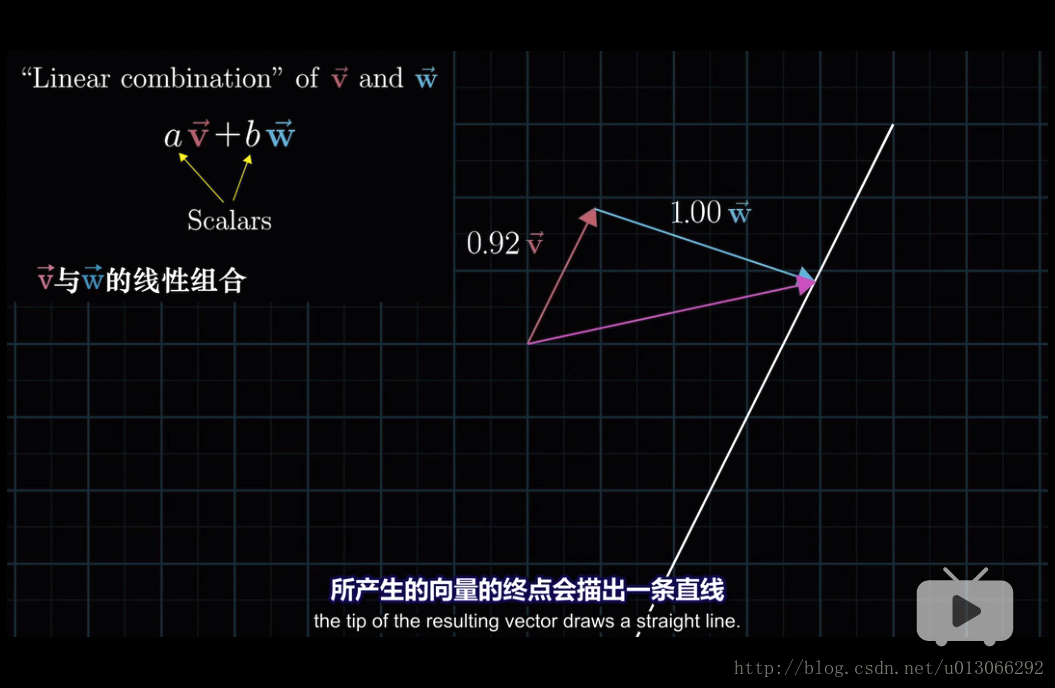
2.2 線性組合
2.2.1 如何理解“線性”這個詞?
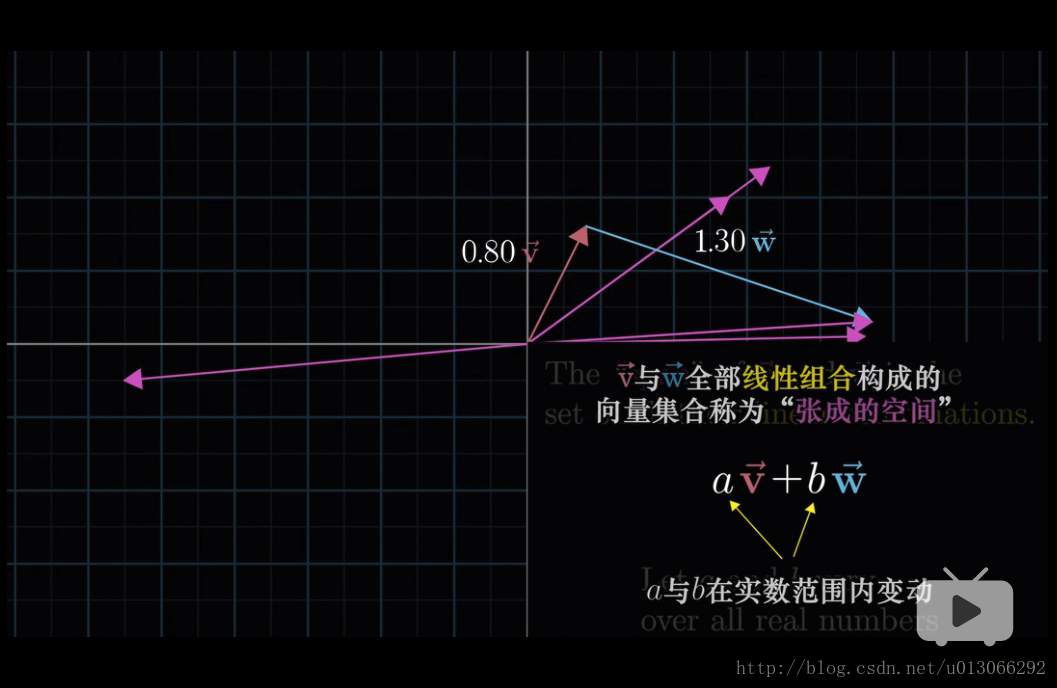
2.3 張成的空間
以兩個向量為例:
像在大部分的二維裡,向量張成的空間是一個二維平面;
如果向量在同一條直線上,那麼它們張成的空間也就是一條線。
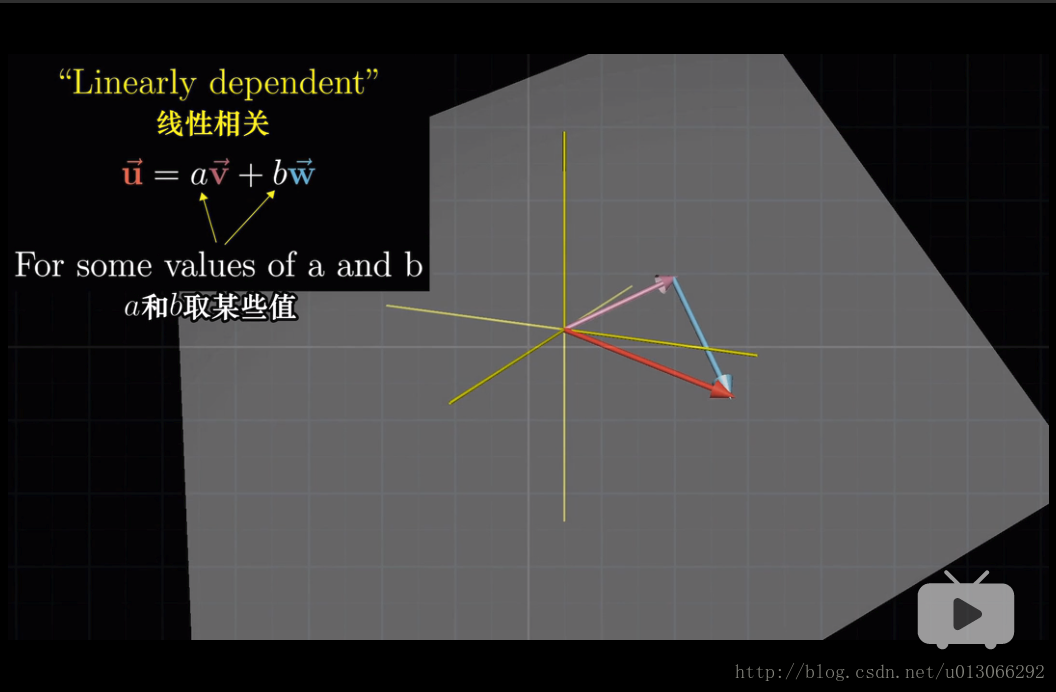
2.4 線性相關
當一個向量的變化並不會影響其它向量張成的空間改變,即稱為線性相關。(應該就是這個向量的變化一直出現在其它向量張成的空間裡。)
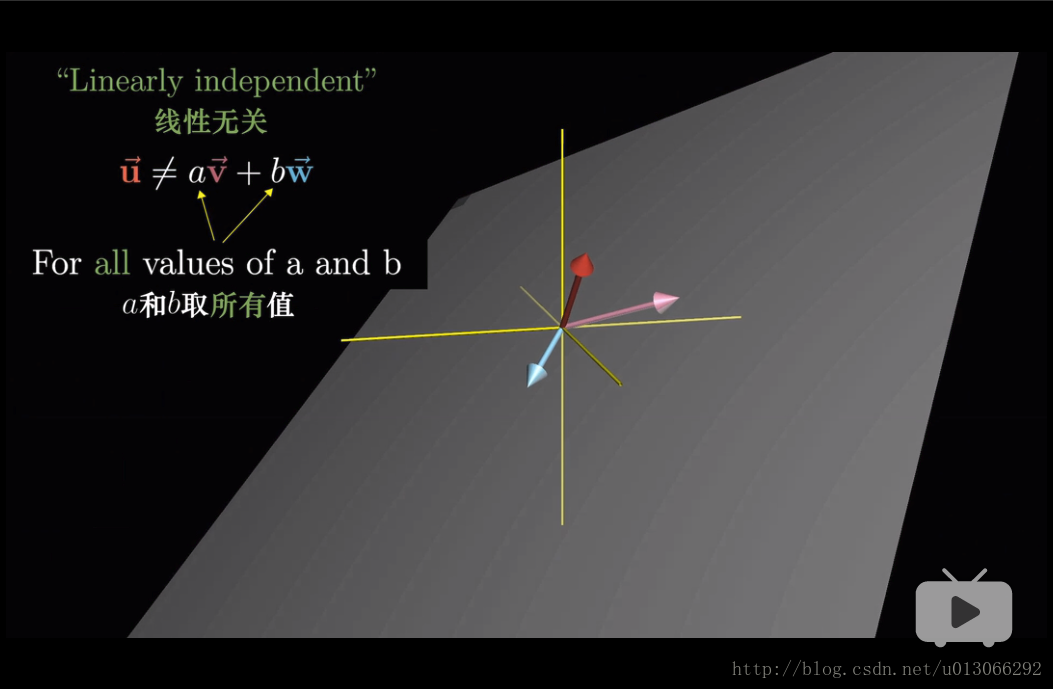
當一個向量的變化會改變其它向量張成的空間,即稱為線性無關。(這個向量的變化沒有在其它向量張成的空間裡。)
2.5 基的嚴格定義
3. 矩陣與線性變換
3.1 線性變換
就是一個向量通過變換
這裡變換跟函式是一個意思,用變換這個詞能讓我們從運動的角度來分析。
滿足兩個條件即可認為是線性變換:
3.2 如何用數值描述線性變換?
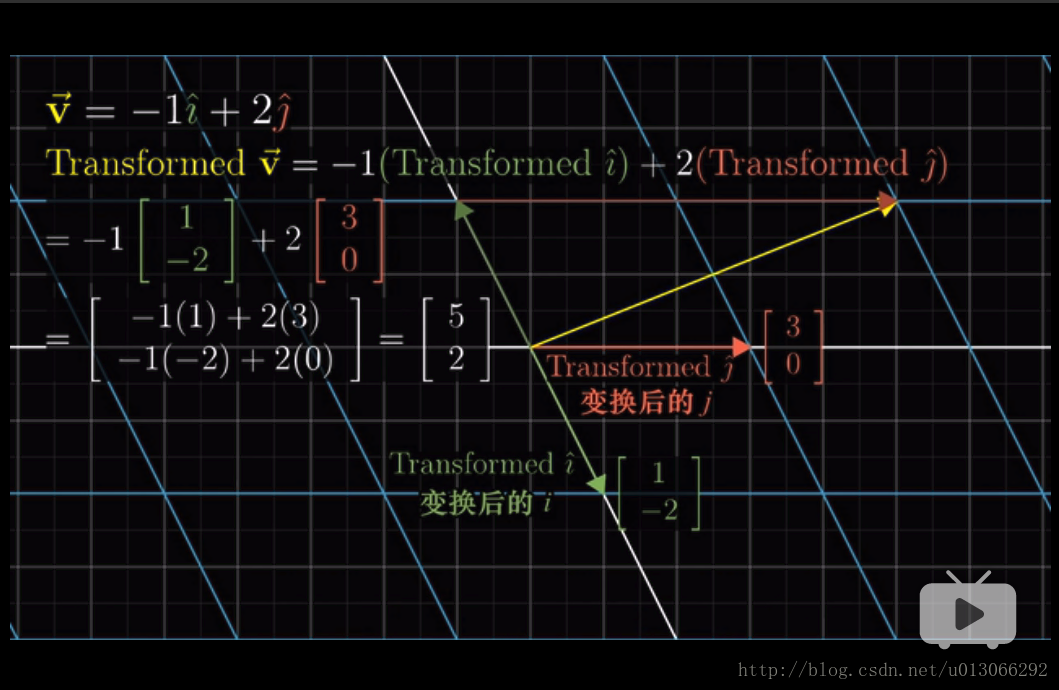
只需要記住兩個基向量變換後的位置即可,其它向量都會隨之移動。
也就是說,假定在原來的座標(基向量為(1,0)和(0,1))裡有一個向量(x , y),我們想知道它通過線性變換後,是會出現在什麼位置?
那麼就可以通過先知道變換後的基向量的位置(基向量變為(a,c)和(b,d)),再將基向量跟這個向量進行線性組合即可。
這種操作可以稱為矩陣向量乘法
4. 矩陣乘法與線性變換複合
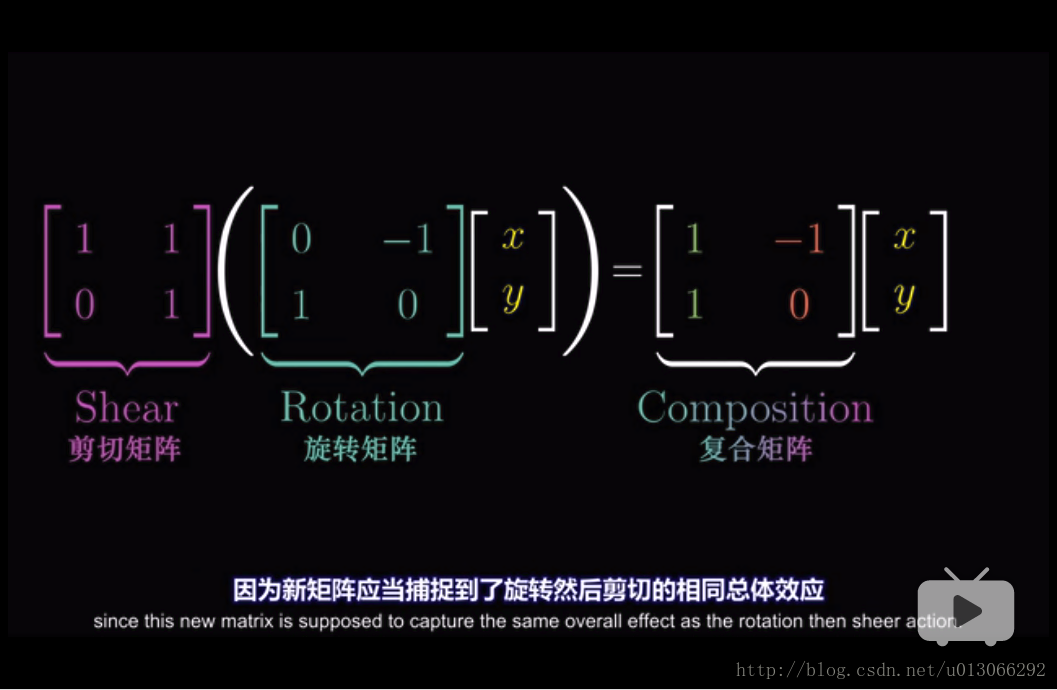
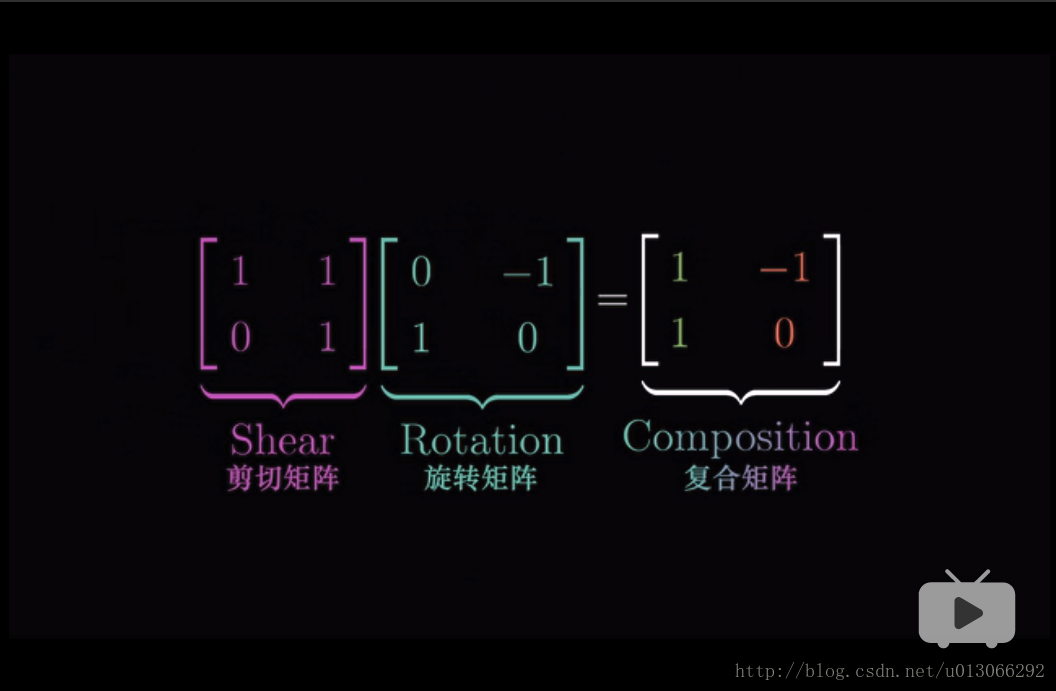
多次變換(假設先旋轉再剪下)後的矩陣其實也就是一個複合的矩陣。
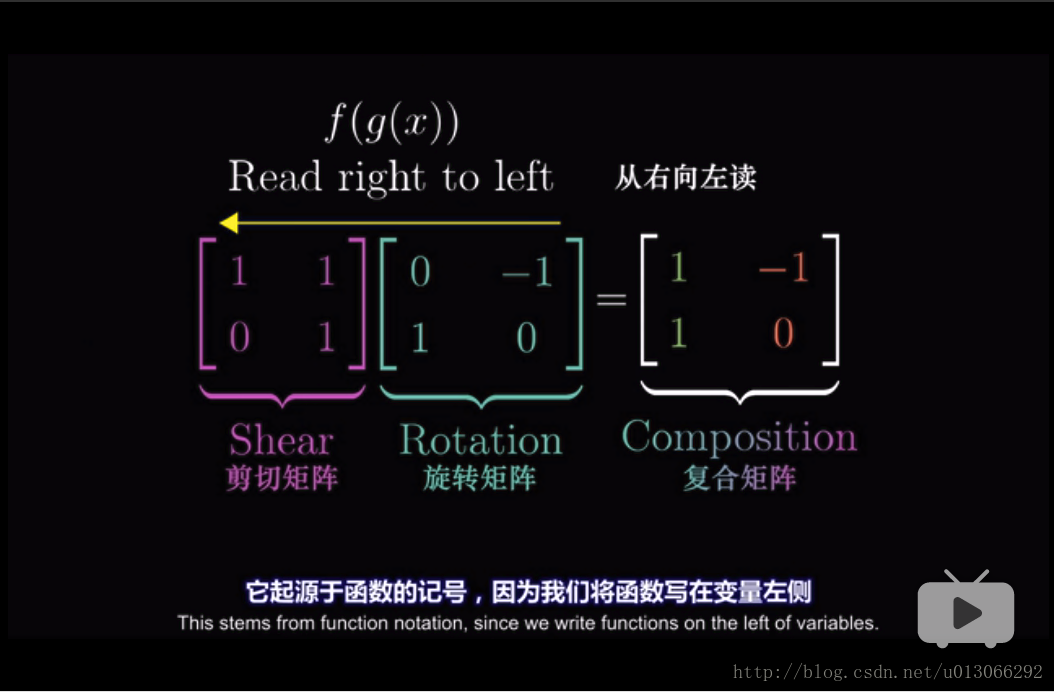
可以看到這裡的變換函式是從右往左新增,是因為函式的記號(記得我們在上面說變換即函式):
普適性地來看複合矩陣的計算:
把 左邊矩陣 看作是 右邊矩陣 變換後的 基向量。
這裡不滿足乘法交換律。
即先旋轉再剪下 跟 先剪下再旋轉 得到的效果是不一樣的。
M1M2 ≠ M2M1
(這裡有個地方是我一開始想不明白,就是我一開始對這個變換想成了是通過改變基向量來實現變換,但其實不對,基向量的改變是變換後的結果,而不是變換的原因。所以在用幾何考慮變換的時候,不應該去改變基向量,而要考慮的是整個座標的變換後,才去看基向量的改變結果)
符合乘法結合律。
(AB)C = ABC