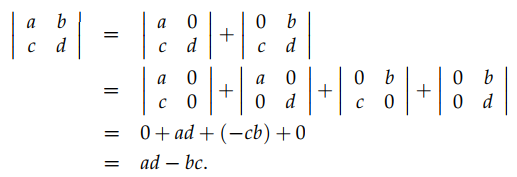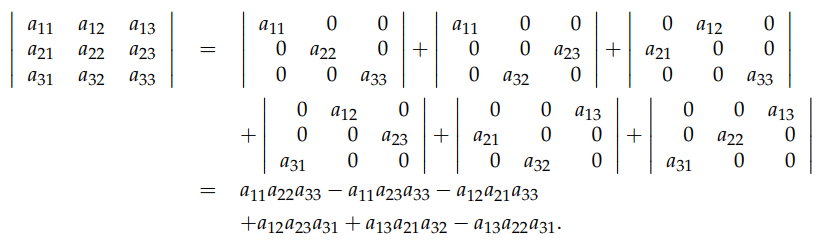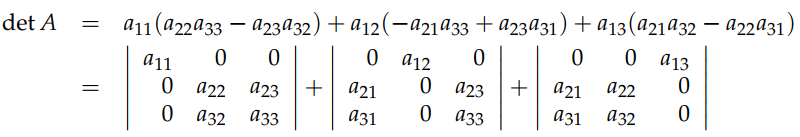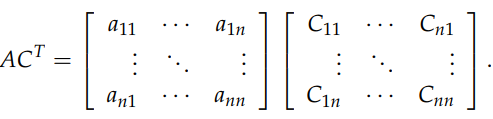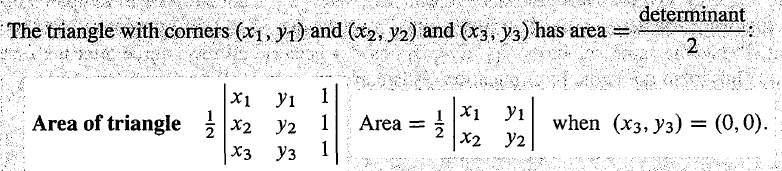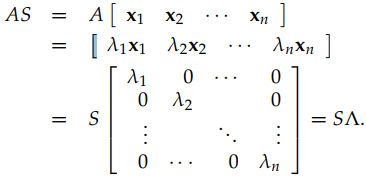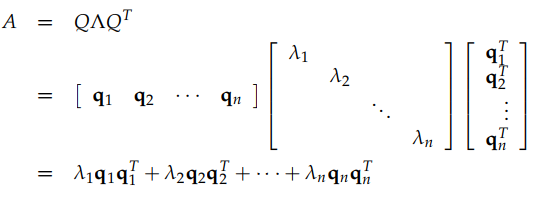引言

終於到了課程的後半部分，它的主題是關於 determinants 和 eigenvalues 的。

Properties of Determinants

教授在整個 lecture 18 中介紹了 Determinants 的10個屬性。The determinant is a number associated with any square matrix; we’ll write it as det A or |A|. 文章 summary 中已經把這10個屬性整理地很清楚了，沒有什麼好補充的了。

Determinant Formulas and Cofactors

通過上個小節中介紹的屬性 3(b)，可以推匯出求 2×2 矩陣的行列式的公式，如下圖所示。從這個推導過程中可以看出，我們先拆分第一行，得到2個矩陣，然後再把得到的這個2個矩陣分別拆分得到4個矩陣。

從這個模式中，不難得到3×3矩陣的行列式的公式：我們先拆分第一行，會得到3個矩陣，然後再分別拆分這3個矩陣的第2行，就會得到9個矩陣，然後再分別拆分這9個矩陣的第3行，會得到27個矩陣。幸運的是，這27個矩陣中會得到很多的0，就像2×2 矩陣那樣，問題是哪些矩陣會是0呢？從那個2×2 矩陣就可以看出來，同一列上存在超過1個非0元素的矩陣就會為0。因此，這個3×3的矩陣的非0項有 3!=6 個，因此對於 n×n 的矩陣來說，就有 n! 個非0項。這是因為，第1行有n種選擇，由於它佔了一列，第2行就只有 n-1 種選擇了，以此類推，你動手試試馬上就明白了。

Cofactor formula 實際上就是重寫我們上面得到的 determinant Formulas，下圖中是沿著 row 1 的 cofactor，你也沿著其它的 rows 計算，哪個 rows 更容易得到矩陣的 determinant 就用哪個。在下圖可以看到，第1行的每個元素乘以括號中的 cofactors

，不難發現，each cofactor is (plus or minus) the determinant of a 2×2 matrix. 那麼如何決定是正的還是負的 determinant 呢？用 (−1)i+j，比如下圖中的例子，a11 的 cofactor 就是正的 determinant，由於i=1，j=1; 而對於a12 的 cofactor 就是負的 determinant，由於i=1，j=2，你可以做一下 Exercises on determinant formulas and cofactors 中的練習題來鞏固一下公式。

在這個 lecture 中，教授用上面得到的公式計算了一下 Tridiagonal matrix 的行列式，we get a sequence which repeats every six terms. 計算過程也很簡單，請參考：

Tridiagonal matrix

無論是 Determinant Formulas and Cofactors 都是用來求一個矩陣的 determinant 的，對於一個矩陣來說，哪個簡單就用哪個方法求解。

Cramer’s Rule, Inverse Matrix and Volume

在前面的小節中，我給出了一個求矩陣的逆的演算法，即通過對 [A|I]→[I|A−1] 消元轉換的過程。至此，我們可以通過先前學過的知識來得出一個 formula for A−1，下面公式中的 CT 是 cofactors

A−1=1detACT

要想證明上述公式的正確性，只需要證明 (detA)I=ACT，如下圖所示，矩陣的第1行 × CT 的第1列實際上就是求矩陣 A 的行列式的 Cofactors 公式，即 detA, 矩陣的第2行 × CT 的第2列也是求矩陣 A 的行列式的 Cofactors 公式，以此類推，ACT 得到的矩陣對角線上應該全部是 det A，接下來如何證明其它的元素都是0呢？其實也很簡單，如果你讓矩陣的第1行 × CT 的第2列實際上就是矩陣V的行列式，這裡矩陣 V 就是把原來矩陣A的第2行用A的第1行取替掉，這就導致了 V 的第1行和第2行相等，因此V是一個 singular 的矩陣，所以 det V=0. 同樣的道理，你讓矩陣的第1行 × CT 的第3列實際上也是一個矩陣的行列式，這次只不過是把原來矩陣A的第3行用A的第1行取替掉，以此類推。這會導致對角線以外的元素都是0，因此公式可證。

如果你已經理解了 cofactors，Cramer’s Rule 也很好理解，實際的計算中它並沒有多大作用，它只不過給了另一種角度去看待公式。計算 inverses 還是用消元來的更有效，這裡就不多說它了。

最後是行列式與體積之間的關係：|det A|=volume of box, box 的邊是矩陣 A 的列向量。在前面，我已經總結了關於行列式的10個屬性，後7個屬性是前面3個屬性衍生出來的，因此想證明它們的關係，我們只需要證明 volume of box 也滿足前面3個屬性，證明很簡單，不多說了，看一下 lecture 20 馬上就能明白了。給出三角形3個頂點的座標，下圖是用行列式計算其面積的公式，在某些情況下，用行列式計算面積要比直接算更為簡單，這個公式也更容易記住。同時建議參考一下我總結的多變數微積分的小節：

Eigenvalues and Eigenvectors

從幾何的角度看 eigenvectors：當矩陣 A 作用於向量 x 時，輸出的結果平行 x. 寫成代數的形式就是：Ax=λx，這裡的 x 是矩陣 A 的特徵向量; λ 是矩陣 A 的特徵值。從這個公式不難看出，所有的向量都是 identity matrix 的特徵向量，所有的特徵值 = 1。注意：特徵向量應該是 non-zero 向量。由於等式中有2個未知量（x 和 λ），我們需要點技巧來解等式。

首先，把等式變換成：Ax−λx=(A−λI)x=0，現在很明顯，我們要求的特徵向量 x 就是 A−λI 的 nullspace，因此要想 nullspace 有 non-zero 的解，A−λI 必須是 singular. 即，det(A−λI)=0, 求出 λ 以後，接著就可以求出特徵向量 x 了。

接下來談談矩陣的對角化。If A has n linearly independent eigenvectors, we can put those vectors in the columns of a (square, invertible) matrix S. 如下圖所示，我們可以得到：AS=SΛ，因此 A=SΛS−1

接下來談談矩陣 A 的指數。一種角度是：如果 Ax=λx, 那麼 A2x=λAx=λ2x. 另一種角度是：A2=SΛS−1SΛS−1=SΛ2S−1. 因此可得結論： A 的 k 次冪，它的特徵向量保持不變，而特徵值也變成了 k 次冪。我們還可以得到另一個結論：就是當 |λ|<1,k→∞ 時， Ak→0

從上面的推導過程可以看到，上面得到的所有結論依賴一個條件：A 要有 n 個 independent eigenvectors，否則結論都不成立。如果矩陣 A 的所有 eigenvalues 都不相同，那麼它就保證有 n 個 independent eigenvectors. 幸運的是，大多數的矩陣都會有不同的 eigenvalues.

注意：從 Ax=λx 可以看出，有一個特徵向量可以得到一個特徵值，即一個特徵向量對應一個特徵值; 但是，多個特徵向量有可能對應相同的特徵值（比如單位矩陣或者 Finding Eigenvectors with repeated Eigenvalues 中的例子），反過來說是不成立的（多個特徵值對應同一個特徵向量）。

Eigenvalues 和 Eigenvectors 的重要屬性

1、Eigenvectors with Distinct Eigenvalues are Linearly Independent

2、Singular Matrices have Zero Eigenvalues

3、假設矩陣A是一個大小為n，nonsingular 的方陣，那麼它具有下面的性質：

• A row-reduces to the identity matrix
• The null space of A contains only the zero vector
• The linear system has a unique solution for every possible choice of b
• The columns of A are a linearly independent set
• The rank of A is n
• The determinant of A is nonzero
• λ=0 is not an eigenvalue of A

4、Suppose A is a square matrix and λ is an eigenvalue of A, then αλ is an eigenvalue of αA

5、Suppose A is a square nonsingular matrix and λ is an eigenvalue of A, then 1λ is an eigenvalue of the matrix A−1

6、Suppose A is a square matrix and λ is an eigenvalue of A, then λ is also an eigenvalue of the matrix AT

7、Suppose that A is a square matrix of size n, then A cannot have more than n distinct eigenvalues.

8、如果一個矩陣的特徵值沒有0存在（即它不是 Singular），那麼它就有 full rank n; 反之，如果它的特徵值有0，那麼它的 rank=n-r，其中 r 是 nullsapce 的 dimension.

9、特徵值的和 = trace

10、特徵的乘積 = 行列式

Symmetric Matrices and Positive Definiteness

如果一個矩陣有特殊的屬性，那麼它的特徵值和特徵向量很有可能有特徵的屬性。對於 Symmetric Matrices 的特徵值和特徵向量來說，它有以下2個特殊屬性：

• A symmetric matrix has only real eigenvalues
• The eigenvectors can be chosen orthonormal

教授在課上給出了屬性1的證明，很簡單，這裡就不總結了，屬性2教授的書中也給出了證明。有了上面的這2個屬性，我們就可以把上面得到的對角化公式，A=SΛS−1，改寫成 A=QΛQ−1=QΛQT，接著我們可以得到下圖中的推導。如果你忘記了矩陣的乘法，參看一下 Perspective 4: columns × rows

通過上圖的結果可以總結出：The matrix qk

相關推薦

MIT 18.06 線性代數總結（Part II）

引言 終於到了課程的後半部分，它的主題是關於 determinants 和 eigenvalues 的。 Properties of Determinants 教授在整個 lecture 18 中介紹了 Determinants 的10個屬性。The

MIT 18.06 線性代數總結（Part I）

Overview The Geometry of Linear Equations 教授在這個 lecture 中介紹了3個概念：Row Picture，Column Picture, and Matrix Picture，其中理解

線性代數-總結（一）

線性代數的核心內容就是線性變換，前面主要從靜態和動態兩個方面進行描述，奇異值分解應該比矩陣對角化更為一般，矩陣對角化只是它的特殊情

線性代數二（基本概念）

八、矩陣的秩： 1、矩陣子式的定義與子式個數的計算：                       概念：矩陣中最高非零子式的階數。 2、矩陣秩的定義：  

線性代數一（基本概念）

一、線性代數基本知識： 1、線性：                 數乘運算與加法運算 呈現 線性。 2、 二、向量： 1、向量的表示方法：        

2019最新專為程式設計師設計的線性代數課程（已更新）

第1章 歡迎大家來到《專給程式設計師設計的線性代數》 歡迎大家來到《專給程式設計師設計的線性代數》，在這個課程中，我們將使用程式設計的方式，學習線性代數，這個近現代數學發展中最為重要的分支。學懂線性代數，是同學們深入學習人工智慧，機器學習，深度學習，圖形學，影象學，密碼學，等等諸多領域的基礎。

線性表總結（c語言）

線性表 線性表特點 存在一個唯一的一個被稱作”第一個”的資料元素 存在唯一的一個被稱做”最後一個”的資料元素 除第一個之外，集合中的每個資料元素均只有一個前驅 除最後一個之外，集合中每個資料元素均只有一個後繼 定義 一個線性表是n個數據元素的

如何使用UIAutomation進行iOS 自動化測試（Part II）

3. 經驗分享（讓你生活變得更簡單） 類庫Tune-up介紹 現在你應該基本上知道如何編寫測試程式碼了。但你慢慢地會發現，你會經常寫到一些重複的，冗餘的，黏糊糊的程式碼，像下面一樣： 1 2 3

VXLAN 概念（Part II）- 每天5分鐘玩轉 OpenStack（109）

上一節我們介紹了 VXLAN 的封裝格式以及 VTEP。 今天我們將通過例子討論 VXLAN 封裝和轉發包的過程，以及 Linux 對 VXLAN 的原生支援。 VXLAN 包轉發流程 VXLAN 在 VTEP 間建立隧道，通過 Layer 3 網

MIT 18.06 ODE video note(part I)

////////////////////////////////////////////////////////  :05 2013-11-5 Tuesday  ODE == Ordinary Differential Equations    9:06 2013-11-5

PYTHON替代MATLAB線上性代數學習中的應用(使用Python輔助MIT 18.06 Linear Algebra學習)

 #### 前言 MATLAB一向是理工科學生的必備神器，但隨著中美貿易衝突的一再升級，禁售與禁用的陰雲也持續籠罩在高等學院的頭頂。也許我們都應當考慮更多的途徑，來輔助我們的學習和研究

【高斯消元】CDOJ1785 曜醬的線性代數課堂（三）

++i for cnblogs mes swa eps mem else 正在 高斯消元求行列式板子。 #include<cstdio> #include<cmath> #include<algorithm> #include

【高斯消元】CDOJ1783 曜醬的線性代數課堂（一）

turn abs swap size wap n) memset efi 高斯 高斯消元求逆矩陣板子。 #include<cstdio> #include<cmath> #include<algorithm> #include

【高斯消元】CDOJ1784 曜醬的線性代數課堂（二）

cst %d can cstring 課堂 esp 線性 memset () 高斯消元求矩陣秩板子。 #include<cstdio> #include<cmath> #include<algorithm> #include&

15/18位身份證號碼驗證的正則表達式總結（詳細版）

校驗碼 輸入 詳細 wid width adding 方式 http 效率 前言 開發過程中，常常需要對一些輸入信息進行有效性驗證，使用正則表達式進行校驗是最簡單、效率最高的方式了，下面就來看看15/18位身份證號碼驗證的正則表達式吧。 介紹 xxxxxx yyyy MM

Unity學習（三）Unity Shader入門（基礎知識篇）+線性代數複習（未完待續）

至於為什麼剛建立了指令碼，現在就要做Shader了。。說多了都是淚 1.建立一個新的材質 Material Assert -> Create -> Material 拖到Scene中的某個物體上 2.建立一個新的Shader Assert -> Create -

機器學習中的線性代數知識（下）

關於作者 作者小碩一枚，研究方向為機器學習與自然語言處理，歡迎大家關注我的個人部落格https://wangjie-users.github.io/，相互交流，一起學習成長。 前言 在機器學習中的線性代數知識（上）一文中，主要講解了矩陣的本質，以及對映視角下的特

線性代數基礎（矩陣、範數、正交、特徵值分解、奇異值分解、跡運算）

目錄 基礎概念 矩陣轉置 對角矩陣 線性相關 範數 正交 特徵值分解 奇異值分解 跡運算 行列式 如果這篇文章對你有一點小小的幫助，請給個關注喔~我會非常開心的~ 基礎概念 標量：一個標量就是一個單獨的數字 向量：一個向量就是一列數字 矩

線性代數三（重點）

一、最小二乘法： 1、矩陣、向量的求導法則： 思路：將前面的項看作一個整體，對後面求導後 再展開前面的 整體。 ①行向量對元素進行求導： ②：列向量對元素進行求導： ③矩陣對元素進行求導： ④元素對行向量進行求導： ⑤元素對列、矩陣：類似上述方法。

線性基總結（模板）+ BZOJ 2460

      所謂線性基，就是線性代數裡面的概念。一組線性無關的向量便可以作為一組基底，張起一個線性的向量空間，這個基地又稱之為線性基。這個線性基的基底進行線性運算，可以表示向量空間內的所有向量，也即所有向量可以拆成基底的線性組合。       在ACM領域，線性基主要用來處理