如何理解離散傅立葉變換（一）

——實數形式傅立葉變換

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

本文作者：隨煜而安  二零一五年五月二十三日

原創作者：July、dznlong  

推薦閱讀：

1.The Scientist and Engineer's Guide to Digital Signal Processing

2.July大神部落格

3.dznlong大神部落格

4.高等數學/數學分析中關於傅立葉級數，三角函式正交系的部分內容

5.深入淺出的講解傅立葉變換（個人感覺講的一般，但是配圖很形象幫助理解）  點選開啟連結

說明：

I、本文中闡述的離散傅立葉變換方法是July、dznlong 兩位根據此書：The Scientist and Engineer's Guide to Digital Signal Processing，By Steven W. Smith, Ph.D.而翻譯而成的，此書地址：

II、同時，有相當一部分內容編輯整理自dznlong、July兩位的部落格，本文是根據兩人文章的思路新增上一些個人的想法以及補充一些細節的成果。上面也貼出了其部落格地址，向原創的作者表示致敬。

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

談談傅立葉變換

開始進入正題：

“關於傅立葉變換，無論是書本還是在網上可以很容易找到關於傅立葉變換的描述，但是大都是些故弄玄虛的文章，太過抽象，盡是一些讓人看了就望而生畏的公式的羅列，讓人很難能夠從感性上得到理解”---dznlong，

那麼，到底什麼是傅立葉變換演算法?傅立葉變換所涉及到的公式具體有多複雜列?這篇文章我借鑑兩位大神的思路，並且先不列出一些複雜的公式，一步一步的引出我們要研究的東西，儘量做到通俗易懂。

傅立葉變換（Fourier transform）是一種線性的積分變換。因其基本思想首先由法國學者傅立葉系統地提出，所以以其名字來命名以示紀念。傅立葉變換就是一種變換而已，只是這種變換是從時間轉換為頻率的變化。

傅立葉變換的提出：

傅立葉是一位法國數學家和物理學家，原名是Jean Baptiste Joseph Fourier(1768-1830), Fourier於1807年在法國科學學會上發表了一篇論文，論文裡描述運用正弦曲線來描述溫度分佈，論文裡有個在當時具有爭議性的決斷：任何連續週期訊號都可以由一組適當的正弦曲線組合而成。 當時審查這個論文拉格朗日堅決反對此論文的發表，而後在近50年的時間裡，拉格朗日堅持認為傅立葉的方法無法表示帶有稜角的訊號，如在方波中出現非連續變化斜率。直到拉格朗日死後15年這個論文才被髮表出來。

誰是對的呢？拉格朗日是對的：正弦曲線無法組合成一個帶有稜角的訊號。但是，我們可以用正弦曲線來非常逼近地表示它，逼近到兩種表示方法不存在能量差別，基於此，傅立葉是對的。

我們觀察下圖，直觀的感受一下這個決斷和傅立葉變換究竟在做怎樣的一件事情。（圖片來自：點選開啟連結）

    在這兩幾幅圖中，分別代表了兩個傅立葉變換。最前面黑色的線代表的就是要進行變換的時域上的函式f（t），它可以表示成後面所有彩色表示的正弦波疊加而成的總和。而後面依不同顏色排列而成的正弦波就是組合為f（t）的各個分量。這些正弦波按照頻率從低到高從前向後排列開來，而每一個波的振幅都是不同的。一定有細心的讀者發現了，在兩個正弦波之間可能還有一條直線，那並不是分割線，而是振幅為0的正弦波！也就是說，為了組成特殊的曲線，有些正弦波成分是不需要的，或者說時域上的函式f（t）中不含有這種對應頻率的分量。來看一個更為詳細一些的圖：

    對於每個正弦波分量，如果我們只看它的頻率和幅值。那麼對於所有分量，就形成了一個以頻率為自變數，幅值為因變數的頻率域上的函式F（w），也就是頻域影象。這時，一個時域——頻域的對映就形成了。這個例子中我們可以看出，一個時域上的近似矩形波被分解成了不同頻率分量的正弦波，反過來看，一些不同頻率的正弦波疊加成了一個矩形波。要注意的是，在實際中通常是將時域的函式變換為不同頻率的正弦波和餘弦波的疊加，而不僅僅是一些正弦波的疊加，儘管這並沒有什麼不同，因為我們知道正餘弦是可以互相表示的。

    到此，在沒有任何公式的情況下，我們也大概知曉了傅立葉變換在做怎樣的一件事情。

傅立葉變換分類

   根據原訊號的不同型別，我們可以把傅立葉變換分為四種類別：
1、非週期性連續訊號        傅立葉變換（Fourier Transform） 
2、週期性連續訊號           傅立葉級數(Fourier Series) 
3、非週期性離散訊號       離散時域傅立葉變換（Discrete Time Fourier Transform） 
4、週期性離散訊號           離散傅立葉變換(Discrete Fourier Transform) 

現在我們要列出一些公式了，先觀察即可，後面會做出詳細的解釋。

     1.連續傅立葉變換

     一般情況下，若“傅立葉變換”一詞不加任何限定語，則指的是“連續傅立葉變換”。連續傅立葉變換將平方可積的函式f（t）表示成復指數函式的積分或級數形式。

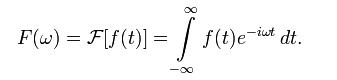
這是將頻率域的函式F(ω)表示為時間域的函式f（t）的積分形式。

連續傅立葉變換的逆變換 (inverse Fourier transform)為：

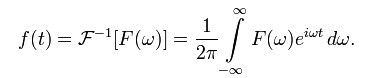
即將時間域的函式f（t）表示為頻率域的函式F(ω)的積分。

2.傅裡葉級數

連續形式的傅立葉變換其實是傅立葉級數 (Fourier series)的推廣，因為積分其實是一種極限形式的求和運算元而已。

對於周期函式，其傅立葉級數是存在的：

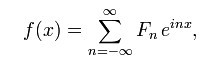
其中Fn為復幅度。對於實值函式，函式的傅立葉級數可以寫成：

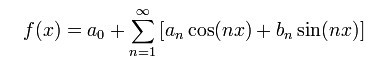
其中an和bn是實頻率分量的幅度。

3.離散時域傅立葉變換
   離散傅立葉變換是離散時間傅立葉變換（DTFT）的特例（有時作為後者的近似）。DTFT在時域上離散，在頻域上則是週期的。DTFT可以被看作是傅立葉級數的逆變換。

4.離散傅立葉變換
   離散傅立葉變換（DFT），是連續傅立葉變換在時域和頻域上都離散的形式，將時域訊號的取樣變換為在離散時間傅立葉變換（DTFT）頻域的取樣。在形式上，變換兩端（時域和頻域上）的序列是有限長的，而實際上這兩組序列都應當被認為是離散週期訊號的主值序列。即使對有限長的離散訊號作DFT，也應當將其看作經過週期延拓成為週期訊號再作變換。在實際應用中通常採用快速傅立葉變換以高效計算DFT。

   為了在科學計算和數字訊號處理等領域使用計算機進行傅立葉變換，必須將函式xn定義在離散點而非連續域內，且須滿足有限性或週期性條件。這種情況下，使用離散傅立葉變換（DFT），將函式xn表示為下面的求和形式：

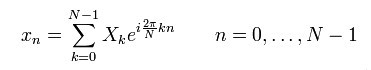
其中Xk是傅立葉幅度。

現在我們已經把四種類型的傅立葉變換的公式給出了，直接看這些公式，就像很多教科書那樣，我想大家跟我一樣都是一頭霧水。 下面是July、dznlong兩位大神給出的一些更為直觀的東西。

我們可以觀察思考下上述傅立葉變換的4種變體的特點

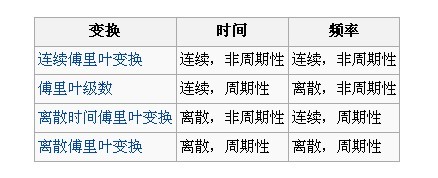
       下圖是四種原訊號圖例（從上到下，依次是FT，FS，DTFT，DFT）：

對於計算機來說只有離散的和有限長度的資料才能被處理。所以首先可以肯定的是，對於計算機中的研究，我們的時域訊號需要是離散的。對於我們要處理的輸入訊號，考慮如果是非週期性訊號的普遍情況。我們需要用無窮多不同頻率的正弦曲線來表示，這對於計算機來說也是不可能實現的。所以頻率域上也要是離散的。所以基於上面的分析，我們下面重點討論和理解的是離散傅立葉變換（DFT），因為只有它才能被計算機適用。

 另外，每種傅立葉變換都分成實數和複數兩種方法，對於實數方法是最好理解的，但是複數方法就相對複雜許多了，需要懂得有關複數的理論知識，不過，如果理解了實數離散傅立葉變換(real DFT)，再去理解複數傅立葉變換就更容易了，所以我們先把複數的傅立葉變換放到一邊去，先來理解實數傅立葉變換，在後面我們會先講講關於複數的基本理論，然後在理解了實數傅立葉變換的基礎上再來理解複數傅立葉變換。所以本文後面的重點是理解實數離散傅立葉變換(real DFT)。

截止到這裡，我們簡單闡述了傅立葉變換的一些基礎知識和思想。後面，我們將從相對簡單的實數傅立葉變換出發，試著去理解它。

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------

實數離散傅立葉變換(real DFT)

首先，先來看一個關於實數離散傅立葉變換(Real DFT)的例子     

通過這個例子，是想引出實數離散傅立葉變換在數學或者說程式中的表達方法，並且如果能理解實數離散傅立葉變換的原理就更好了

下圖是一個實數原始離散訊號影象：

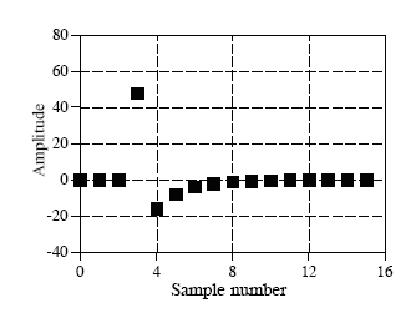
       這個訊號的長度是16，於是可以把這個訊號分解9個餘弦波和9個正弦波（一個長度為N的訊號可以分解成N/2+1個正餘弦訊號，這是為什麼呢？我們稍後再討論，也許結合下圖你就能已經看出其中的原因。參看最後面的證明1）

結合下面的18個正餘弦圖,我想從計算機處理精度上就不難理解，一個長度為N的訊號，最多隻能有N/2+1個不同頻率，再多的頻率就超過了計算機所能所處理的精度範圍），如下圖：

        9個餘弦訊號：

從左至右，從上到下，分別對應著頻率k=0~8；

頻率k=i就代表在長度為N的區間上存在著i個週期。k越大，週期越小。

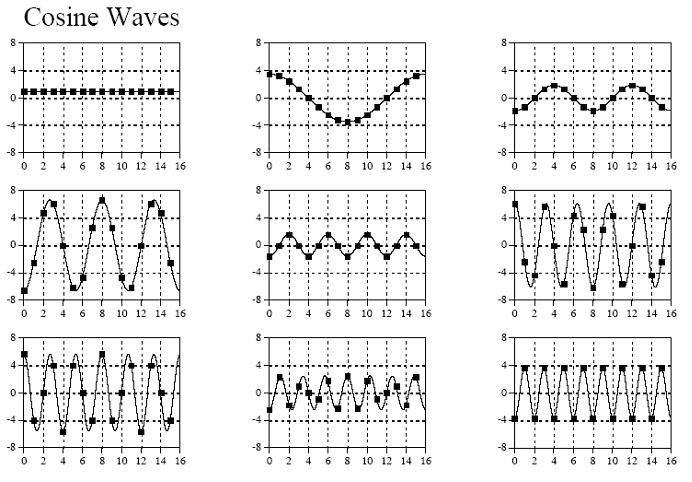
        9個正弦訊號：

同樣的，從左至右，從上到下，分別對應著頻率k=0~8；

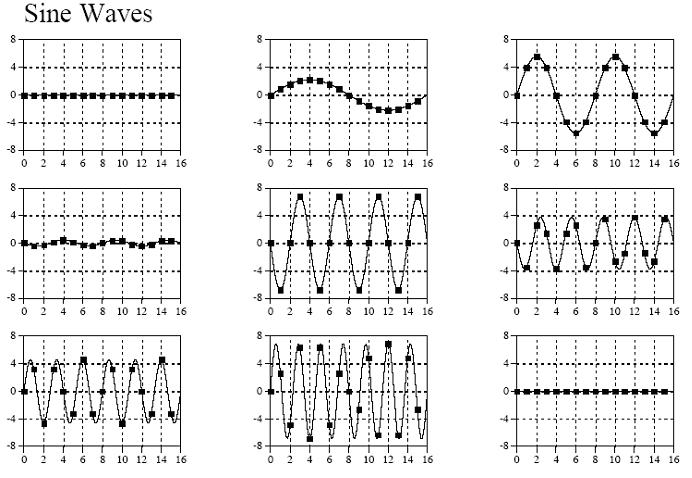
       把以上所有訊號相加即可得到原始訊號，至於是怎麼分別變換出9種不同頻率訊號的，我們也先不急，後面會說到，先看看對於以上的變換結果，在程式中又是該怎麼表示的，我們可以看看下面這個示例圖：

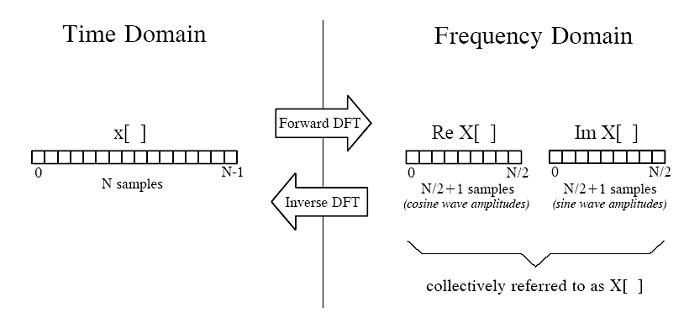
 上圖中左邊表示時域中的訊號，右邊是頻域訊號表示方法，
從左向右，-->，表示正向轉換(Forward DFT)，從右向左，<--，表示逆向轉換(Inverse DFT)，
用小寫x[]表示訊號在每個時間點上的幅度值陣列, 用大寫X[]表示每種頻率的幅度值陣列（即時間x-->頻率X）, 
因為變換到頻率域後有N/2+1種頻率，需要記錄N/2+1個幅值，所以該陣列長度為N/2+1

X[]陣列又分兩種，一種是表示餘弦波的不同頻率幅度值：Re X[]，另一種是表示正弦波的不同頻率幅度值：Im X[]。

其中，Re是實數(Real)的意思，Im是虛數(Imagine)的意思，採用複數的表示方法把正餘弦波組合起來進行表示，但這裡我們不考慮複數的其它作用，只記住是一種組合方法而已，目的是為了便於表達（個人感覺這樣表示是因為更為普遍和常用的複數形式傅立葉變換的存在，為了在形式上契合它）。還有，在後面我們會知道，複數形式的傅立葉變換頻率域陣列長度是N，而不是N/2+1。

到此，實數形式的離散傅立葉變換的表示方法及符號約定我們已經說清楚了，並且變換所做的實際工作我們也心裡有數了。現在，補充上面欠著的關於“一個長度為N的訊號可以分解成N/2+1個正餘弦訊號”的證明1。

這個問題解決了，不過到這裡不知道有沒有人和我有同樣的疑問。為什麼變換後的正弦餘弦分量的頻率取值都正好是整數？這個問題將在下面的學習中自然而然的明白。

實數形式離散傅立葉正變換（DFT）

    由上面的討論我們知道DFT是要將時域長度為N的離散序列x（n）變換為不同頻率取值的正餘弦分量，且頻率K取值為0~N/2+1。其實我們正變換要做的是已知時域序列x（n），求頻率域上的幅度值陣列，也就是ReX[] 和ImX[]。

有三種完全不同的方法進行DFT：一種方法是通過聯立方程進行求解, 從代數的角度看，要從N個已知值求N個未知值，需要N個聯立方程，且N個聯立方程必須是線性獨立的，但這是這種方法計算量非常的大且極其複雜，所以很少被採用；第二種方法是利用訊號的相關性（correlation）進行計算，這個是我們後面將要介紹的方法；第三種方法是快速傅立葉變換（FFT），這是一個非常具有創造性和革命性的的方法，因為它大大提高了運算速度，使得傅立葉變換能夠在計算機中被廣泛應用，但這種演算法是根據複數形式的傅立葉變換來實現的，它把N個點的訊號分解成長度為N的頻域，這個跟我們現在所進行的實域DFT變換不一樣，而且這種方法也較難理解，這裡我們先不去理解，等先理解了複數DFT後，再來看一下FFT。有一點很重要，那就是這三種方法所得的變換結果是一樣的，經過實踐證明，當頻域長度為32時，利用相關性方法進行計算效率最好，否則FFT演算法效率較高。現在就讓我們來看一下相關性演算法。--July
 
利用第一種方法、訊號的相關性(correlation)可以從噪聲背景中檢測出已知的訊號，我們也可以利用這個方法檢測訊號波中是否含有某個頻率的訊號波：把一個待檢測訊號波乘以另一個訊號波，得到一個新的訊號波，再把這個新的訊號波所有的點進行相加，從相加的結果就可以判斷出這兩個訊號的相似程度。如下圖：

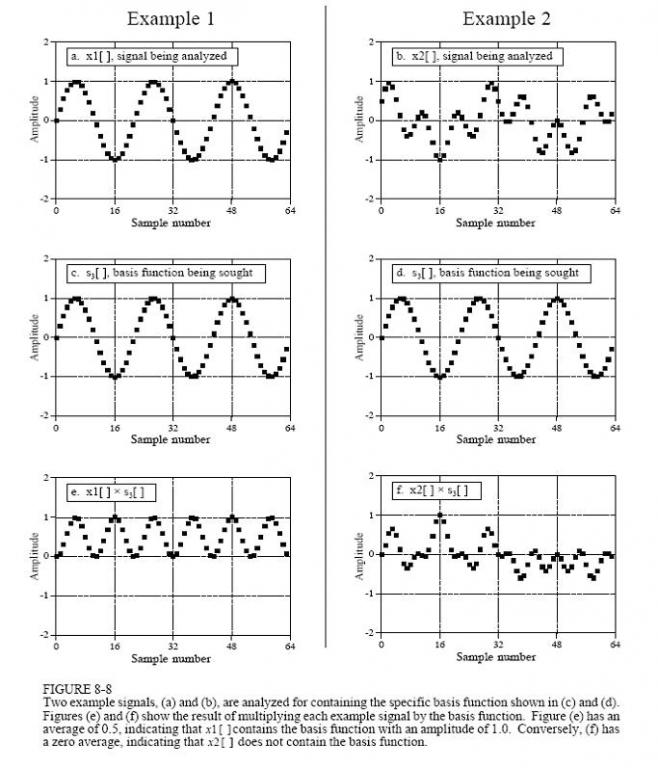
        上面a和 b兩個圖是待檢測訊號波，圖a很明顯可以看出是個3個週期的正弦訊號波，圖b的訊號波則看不出是否含有正弦或餘弦訊號，圖c和d都是個3個週期的正弦訊號波，圖e和f分別是a、b兩圖跟c、d兩圖相乘後的結果，圖e所有點的平均值是0.5，說明訊號a含有振幅為1的正弦訊號c，但圖f所有點的平均值是0，則說明訊號b不含有訊號d。這個就是通過訊號相關性來檢測是否含有某個訊號的方法。
 
       第二種方法：相應地，我也可以通過把輸入訊號和每一種頻率的正餘弦訊號進行相乘（關聯操作），從而得到原始訊號與每種頻率的關聯程度（即總和大小），這個結果便是我們所要的傅立葉變換結果，下面兩個等式便是我們所要的計算方法：

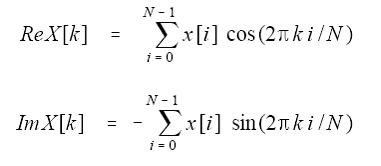
       第二個式子中加了個負號，是為了保持複數形式的一致，前面我們知道在計算時又加了個負號，所以這只是個形式的問題，並沒有實際意義，你也可以把負號去掉，並在計算時也不加負號。

       這裡有一點必須明白一個正交的概念：兩個函式相乘，如果結果中的每個點的總和為0，則可認為這兩個函式為正交函式。要確保關聯性演算法是正確的，則必須使得跟原始訊號相乘的訊號的函式形式是正交的，我們知道所有的正弦或餘弦函式是正交的，這一點我們可以通過簡單的高數知識就可以證明它，所以我們可以通過關聯的方法把原始訊號分離出正餘弦訊號。也就是說，一個帶有多個頻率分量的時域函式f（t）乘以某個頻率的正交基的積分，其實就等於函式中對應這個頻率的分量與這個頻率正交基的積分，也就求出了函式與這個頻率的“關聯度”。當然，其它的正交函式也是存在的，如：方波、三角波等形式的脈衝訊號，所以原始訊號也可被分解成這些訊號，但這只是說可以這樣做，卻是沒有用的。

實數形式離散傅立葉逆變換——合成運算方法(Real Inverse DFT) 

DFT合成等式（合成原始時間訊號，頻率-->時間，逆向變換）：

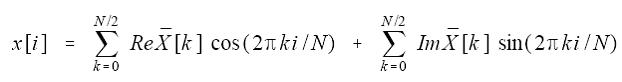
如果有學過傅立葉級數，對這個等式就會有似曾相識的感覺，不錯！這個等式跟傅立葉級數是非常相似的：

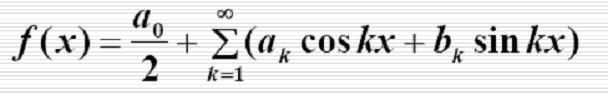
        當然，差別是肯定是存在的，因為這兩個等式是在兩個不同條件下運用的，至於怎麼證明DFT合成公式，這個我想需要非常強的高等數學理論知識了，這是研究數學的人的工作，對於普通應用者就不需要如此的追根究底了，但是傅立葉級數是好理解的，我們起碼可以從傅立葉級數公式中看出DFT合成公式的合理性。                          
       DFT合成等式中的Im X[k]和Re X[k]跟之前提到的Im X[k]和Re X[k]是不一樣的，下面是轉換方法（關於此公式的解釋，見下文）:

       
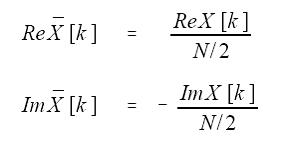
       但k等於0和N/2時,實數部分的計算要用下面的等式:

              
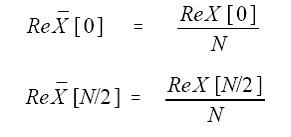
       上面四個式中的N是時域中點的總數，k是從0到N/2的序號。
       為什麼要這樣進行轉換呢？這個可以從頻譜密度(spectral density)得到理解，如下圖就是個頻譜圖：

       
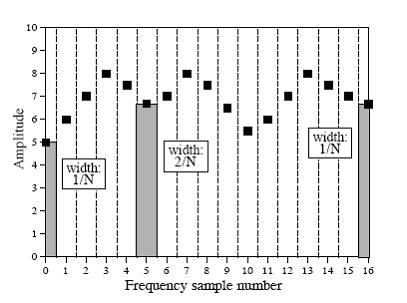
       這是一個頻譜圖，橫座標表示頻率大小，縱座標表示振幅大小，原始訊號長度為N（這裡是32），經DFT轉換後得到的17個頻率的頻譜，頻譜密度表示每單位頻寬中為多大的振幅，那麼頻寬是怎麼計算出來的呢？看上圖，除了頭尾兩個，其餘點的所佔的寬度是2/N，這個寬度便是每個點的頻寬，頭尾兩個點的頻寬是1/N,而Im X[k]和Re X[k]表示的是頻譜密度，即每一個單位頻寬的振幅大小，但表示2/N（或1/N）頻寬的振幅大小，所以分別應當是Im X[k]和Re X[k]的2/N（或1/N）。
 
頻譜密度就象物理中物質密度，原始訊號中的每一個點就象是一個混合物，這個混合物是由不同密度的物質組成的，混合物中含有的每種物質的質量是一樣的，除了最大和最小兩個密度的物質外，這樣我們只要把每種物質的密度加起來就可以得到該混合物的密度了，又該混合物的質量是單位質量，所以得到的密度值跟該混合物的質量值是一樣的。--dznlong
 
       至於為什麼虛數部分是負數，這是為了跟複數DFT保持一致，這個我們將在後面會知道這是數學計算上的需要（Im X[k]在計算時就已經加上了一個負號（稍後，由下文，便可知），再加上負號，結果便是正的，等於沒有變化）。
 
       如果已經得到了DFT結果，這時要進行逆轉換，即合成原始訊號，則可按如下步驟進行轉換：
1、先根據上面四個式子計算得出的值；
2、再根據DFT合成等式得到原始訊號資料。

 到此為止，我們對傅立葉變換便有了感性的認識了。但是，這只是在實域上的離散傅立葉變換，其中雖然也用到了複數的形式，但那只是個替代的形式，並無實際意義，現實中一般使用的是複數形式的離散傅立葉變換，且快速傅立葉變換是根據複數離散傅立葉變換來設計演算法的。隨著作者之後的學習，再總結出後面的博文。