[經典面試題]完美洗牌演算法
題目
有個長度為2n的陣列{a1,a2,a3,…,an,b1,b2,b3,…,bn},希望排序後{a1,b1,a2,b2,….,an,bn},請考慮有無時間複雜度o(n),空間複雜度0(1)的解法。
來源
2013年UC的校招筆試題
思路一
第①步、確定b1的位置,即讓b1跟它前面的a2,a3,a4交換:
a1,b1,a2,a3,a4,b2,b3,b4
第②步、接著確定b2的位置,即讓b2跟它前面的a3,a4交換:
a1,b1,a2,b2,a3,a4,b3,b4
第③步、b3跟它前面的a4交換位置:
a1,b1,a2,b2,a3,b3,a4,b4
b4已在最後的位置,不需要再交換。如此,經過上述3個步驟後,得到我們最後想要的序列。但此方法的時間複雜度為O(n^2)
程式碼一
/*---------------------------------------------
* 日期:2015-02-13
* 作者:SJF0115
* 題目: 完美洗牌演算法
* 來源:2013年UC的校招筆試題
* 部落格:
-----------------------------------------------*/
#include <iostream>
using namespace std;
class Solution {
public:
void PerfectShuffle(int *A,int n){
if 思路二
我們每次讓序列中最中間的元素進行兩兩交換。還是上面的例子:
a1,a2,a3,a4,b1,b2,b3,b4
第①步:交換最中間的兩個元素a4,b1:
a1,a2,a3,b1,a4,b2,b3,b4
第②步:最中間的兩對元素各自交換:
a1,a2,b1,a3,b2,a4,b3,b4
第③步:交換最中間的三對元素:
a1,b1,a2,b2,a3,b3,a4,b4
此思路同上述思路一樣,時間複雜度依然為O(n^2)。仍然但不到題目要求。
程式碼二
/*---------------------------------------------
* 日期:2015-02-13
* 作者:SJF0115
* 題目: 完美洗牌演算法
* 來源:2013年UC的校招筆試題
* 部落格:
-----------------------------------------------*/
#include <iostream>
using namespace std;
class Solution {
public:
void PerfectShuffle(int *A,int n){
if(n <= 1){
return;
}//if
//
int left = n - 1,right = n;
// 交換次數
for(int i = 0;i < n-1;++i){
for(int j = left;j < right;j+=2){
swap(A[j],A[j+1]);
}//for
--left;
++right;
}//for
}
};
int main() {
Solution solution;
int A[] = {1,2,3,4,5,6,7,8,9,10};
solution.PerfectShuffle(A,5);
for(int i = 0;i < 10;++i){
cout<<A[i]<<" ";
}//for
cout<<endl;
}思路三(完美洗牌演算法)
玩過撲克牌的朋友都知道,在一局完了之後洗牌,洗牌人會習慣性的把整副牌大致分為兩半,兩手各拿一半對著對著交叉洗牌。
2004年,microsoft的Peiyush Jain在他發表一篇名為:“A Simple In-Place Algorithm for In-Shuffle”的論文中提出了完美洗牌演算法。
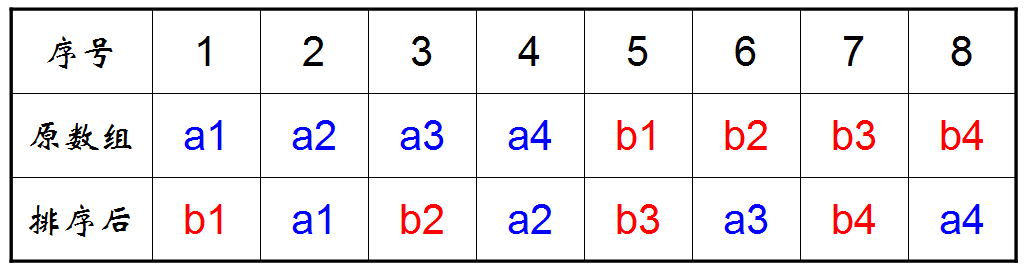
什麼是完美洗牌問題呢?即給定一個數組a1,a2,a3,…an,b1,b2,b3..bn,最終把它置換成b1,a1,b2,a2,…bn,an。這個完美洗牌問題本質上與本題完全一致,只要在完美洗牌問題的基礎上對它最後的序列swap兩兩相鄰元素即可。
(1)對原始位置的變化做如下分析:
(2)依次考察每個位置的變化規律:
a1:1 -> 2
a2:2 -> 4
a3:3 -> 6
a4:4 -> 8
b1:5 -> 1
b2:6 -> 3
b3:7 -> 5
b4:8 -> 7
對於原陣列位置i的元素,新位置是(2*i)%(2n+1),注意,這裡用2n表示原陣列的長度。後面依然使用該表述方式。有了該表示式,困難的不是尋找元素在新陣列中的位置,而是為該元素“騰位置”。如果使用暫存的辦法,空間複雜度必然要達到O(N),因此,需要換個思路。
(3)我們這麼思考:a1從位置1移動到位置2,那麼,位置2上的元素a2變化到了哪裡呢?繼續這個線索,我們得到一個“封閉”的環:
1 -> 2 -> 4 -> 8 -> 7 -> 5 -> 1
沿著這個環,可以把a1、a2、a4、b4、b3、b1這6個元素依次移動到最終位置;顯然,因為每次只移動一個元素,程式碼實現時,只使用1個臨時空間即可完成。(即:a=t;t=b;b=a)
此外,該變化的另外一個環是:
3 -> 6 -> 3
沿著這個環,可以把a3、b2這2個元素依次移動到最終位置。
// 走圈演算法
void CycleLeader(int *a,int start, int n) {
int pre = a[start];
// 2 * i % (2 * n + 1)
int mod = 2 * n + 1;
// 實際位置
int next = start * 2 % mod;
// 按環移動位置
while(next != start){
swap(pre,a[next]);
next = 2 * next % mod;
}//while
a[start] = pre;
}(4)上述過程可以通過若干的“環”的方式完整元素的移動,這是巧合嗎?事實上,該問題的研究成果已經由Peiyush Jain在10年前公開發表在A Simple In-Place Algorithm for In-Shuffle, Microsoft, 2004中。原始論文直接使用了一個結論,這裡不再證明:對於2*n =(3^k-1)這種長度的陣列,恰好只有k個環,且每個環的起始位置分別是1,3,9,…3^(k-1)。
對於上面的例子,長度為8,是3^2-1,因此,只有2個環。環的起始位置分別是1和3。
(5)至此,完美洗牌演算法的“主體工程”已經完工,只存在一個“小”問題:如果陣列長度不是(3^k-1)呢?
若2n!=(3^k-1),則總可以找到最大的整數m,使得m< n,並且2m=(3^k-1)。
對於長度為2m的陣列,呼叫(3)和(4)中的方法整理元素,剩餘的2(n-m)長度,遞迴呼叫(5)即可。
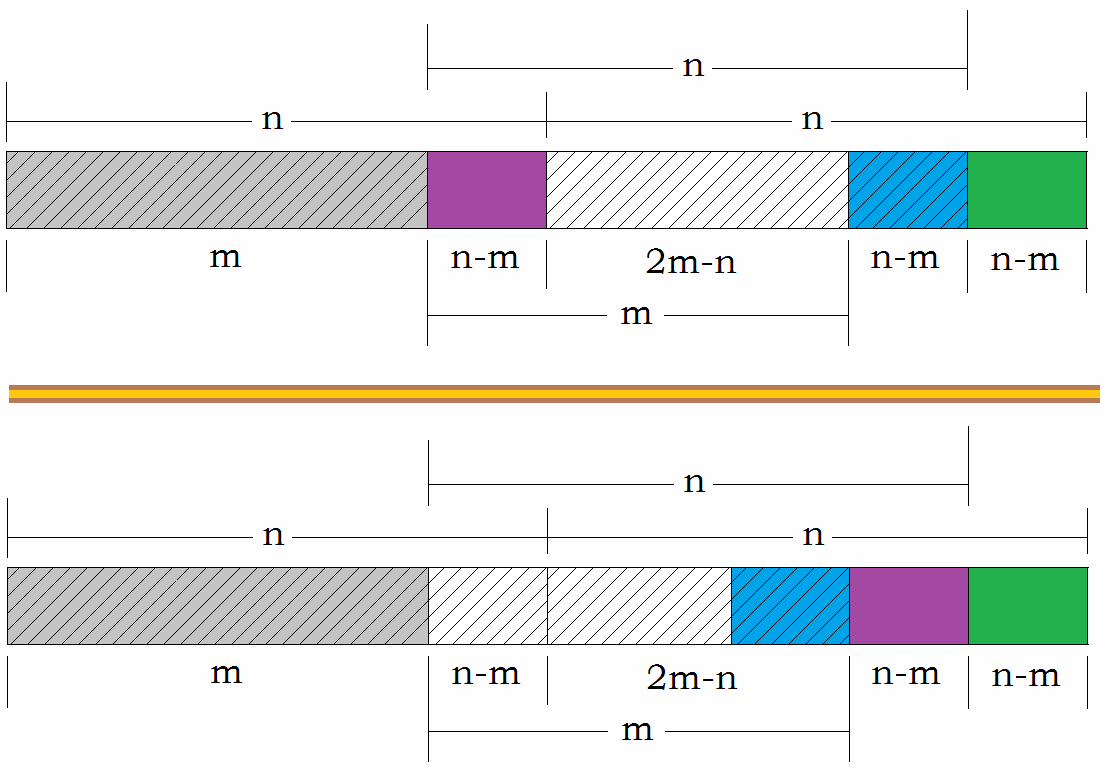
(6)需要交換一部分陣列元素
(下面使用[a,b]表示從a到b的一段子陣列,包括端點)
①圖中斜線陰影部分的子陣列[1,m]應該和[n + 1,n + m]組成一個數組,呼叫(3)和(4)中的演算法;
②陣列[m+1,m+n]迴圈左移n-m次即可。(迴圈位移是存在空間複雜度為O(1),時間複雜度為O(n)的演算法)
(7)原始問題要輸出a1,b1,a2,b2……an,bn,而完美洗牌卻輸出的是b1,a1,b2,a2,……bn,an。解決辦法非常簡單:忽略原陣列中的a1和bn,對於a2,a3,……an,b1,b2,……bn-1呼叫完美洗牌演算法,即為結論。
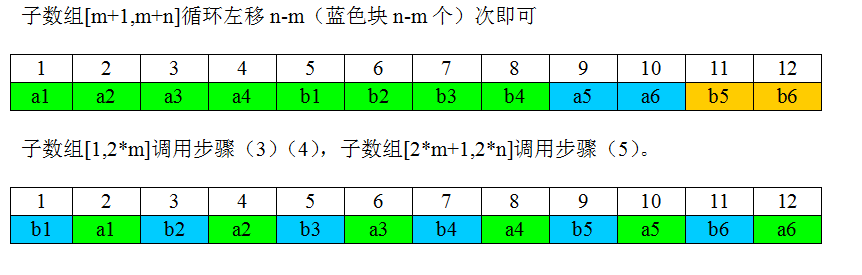
舉個例子: n = 6
a1,a2,a3,a4,a5,a6,b1,b2,b3,b4,b5,b6
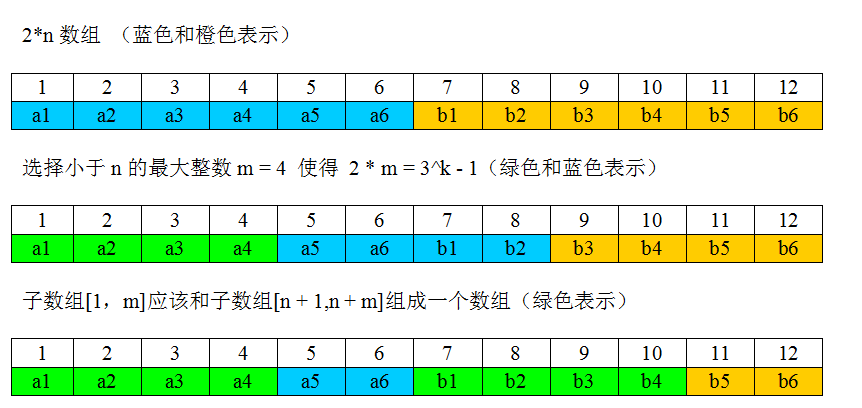
迴圈左移
介紹一下時間複雜度為O(n),空間複雜度為O(1)的迴圈移位操作。
思路:
假設迴圈左移m位。把陣列分成兩段,第一段為前m個元素,第二段為剩餘元素。把第一段和第二段先各自翻轉一下,再將整體翻轉下。
// 翻轉 start 開始位置 end 結束位置
void Reverse(int *a,int start,int end){
while(start < end){
swap(a[start],a[end]);
++start;
--end;
}//while
}
// 迴圈左移m位 n陣列長度 下標從1開始
void LeftRotate(int *a,int m,int n){
// 翻轉前m位
Reverse(a,1,m);
// 翻轉剩餘元素
Reverse(a,m+1,n);
// 整體翻轉
Reverse(a,1,n);
}程式碼:
/*---------------------------------------------
* 日期:2015-02-13
* 作者:SJF0115
* 題目: 完美洗牌演算法
* 來源:2013年UC的校招筆試題
* 部落格:
-----------------------------------------------*/
#include <iostream>
using namespace std;
class Solution {
public:
// 完美洗牌演算法
void PerfectShuffle(int *a,int n){
while(n >= 1){
// 計算環的個數
int k = 0;
// 3^1
int r = 3;
// 2 * m = 3^k - 1
// m <= n -> 2 * m <= 2 * n -> 3^k - 1 <= 2 * n
// 尋找最大的k使得3^k - 1 <= 2*n
while(r - 1 <= 2*n){
r *= 3;
++k;
}//while
int m = (r / 3 - 1) / 2;
// 迴圈左移n-m位
LeftRotate(a+m,n-m,n);
// k個環 環起始位置start: 1,3...3^(k-1)
for(int i = 0,start = 1;i < k;++i,start *= 3) {
// 走圈
CycleLeader(a,start,m);
}//for
a += 2*m;
n -= m;
}
}
private:
// 翻轉 start 開始位置 end 結束位置
void Reverse(int *a,int start,int end){
while(start < end){
swap(a[start],a[end]);
++start;
--end;
}//while
}
// 迴圈右移m位 n陣列長度 下標從1開始
void LeftRotate(int *a,int m,int n){
// 翻轉前m位
Reverse(a,1,m);
// 翻轉剩餘元素
Reverse(a,m+1,n);
// 整體翻轉
Reverse(a,1,n);
}
// 走圈演算法
void CycleLeader(int *a,int start, int n) {
int pre = a[start];
// 2 * i % (2 * n + 1)
int mod = 2 * n + 1;
// 實際位置
int next = start * 2 % mod;
// 按環移動位置
while(next != start){
swap(pre,a[next]);
next = 2 * next % mod;
}//while
a[start] = pre;
}
};
int main() {
Solution solution;
int A[] = {0,1,2,3,4,5,6,7,8,9,10,11,12};
solution.PerfectShuffle(A,6);
for(int i = 1;i <= 12;++i){
cout<<A[i]<<" ";
}//for
cout<<endl;
}拓展一
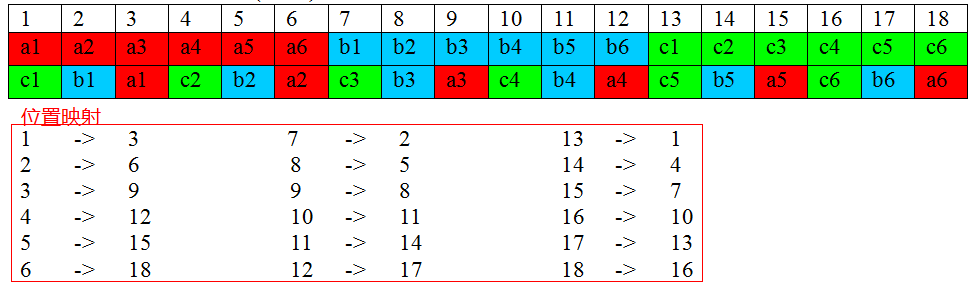
問題:如果輸入是a1,a2,……an, b1,b2,……bn, c1,c2,……cn,要求輸出是c1,b1,a1,c2,b2,a2,……cn,bn,an怎麼辦?
分析: 這個問題本質上其實還是上面的完美洗牌演算法一樣,我們一樣還是分析其規律。
對於原陣列位置i的元素,新位置是(3*i)%(3n+1)
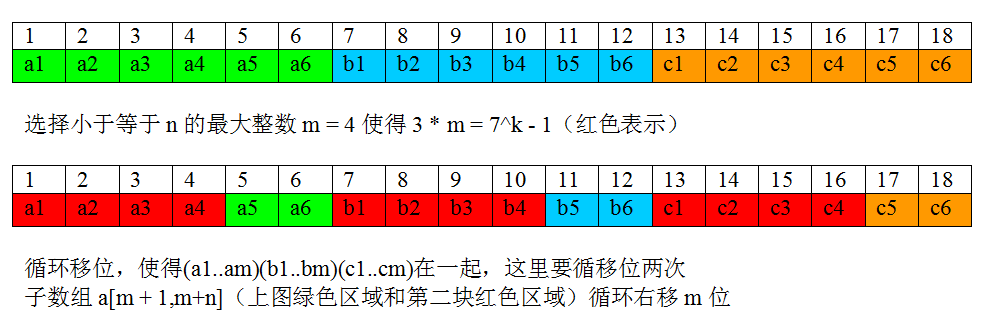
圖中所說的步驟三四五和上面的三四五大體一樣,只是細節不太一樣,看圖就明白了。