史上最全最豐富的“最長公共子序列”、“最長公共子串”問題的解法與思路
花了一天時間把一直以來的“最大子序列”、“最大遞增子序列“、”最大公共子序列“、“最長公共子串”等問題總結了一下。其中參考了若干博文,都備註引用。
首先子序列是指一個一個序列中,由若個數(字母)組成,然後從中任意刪掉幾個數(字母),保留剩下的數(字母)構成了一個序列,即稱子序列。(或者從一個序列中,任意選取若干數或字元,按照這些數或字元原來的排序組成新的序列,即稱子序列)
子串是指在一個字串中任意選取連續的一段字串,即稱子串。
1首先看一下 最大子序列。
最大子序列是要找出由陣列成的一維陣列中和最大的連續子序列。比如{5,-3,4,2}的最大子序列就是 {5,-3,4,2},它的和是8,達到最大;而 {5,-6,4,2}的最大子序列是{4,2},它的和是6。你已經看出來了,找最大子序列的方法很簡單,
參考部落格:int maxSubSum(const vector<int> & arr,int &begin,int &end){ int maxSum=0; int currSum=0; int newbegin=0; for(int i=0;i<arr.size();++i){ currSum+=arr[i]; if(currSum>maxSum){ maxSum=currSum; begin=newbegin; end=i; } if(currSum<0){ currSum=0; newbegin=i+1; } } return maxSum; }
上述這篇部落格中關於“最長遞增子序列”講解的不太好,我自己重新查看了如下的部落格,講解“最長遞增子序列”的內容比較好。
2 最長遞增子序列
最長遞增子序列問題的描述:設L=<a1,a2,…,an>是n個不同的實數的序列,L的遞增子序列是這樣一個子序列Lin=<aK1,ak2,…,akm>,其中k1<k2<…<km且aK1<ak2<…<akm。求最大的m值。
設f(i)表示L中以ai為末元素的最長遞增子序列的長度。則有如下的遞推方程:
這個遞推方程的意思是,在求以ai為末元素的最長遞增子序列時,找到所有序號在L前面且小於ai
public void lis(float[] L)
{
int n = L.length;
int[] f = new int[n];//用於存放f(i)值;
f[0]=1;//以第a1為末元素的最長遞增子序列長度為1;
for(int i = 1;i<n;i++)//迴圈n-1次
{
f[i]=1;//f[i]的最小值為1;
for(int j=0;j<i;j++)//迴圈i 次
{
if(L[j]<L[i]&&f[j]>f[i]-1)
f[i]=f[j]+1;//更新f[i]的值。
}
}
System.out.println(f[n-1]);
}3 重點來了,難點與考點基本都集中在”最長公共子序列“和”最長公共子串“。首先看 最長公共子序列。
必須推薦這篇部落格,用動態規劃思想解最長公共子序列問題,詳細說明了解題方法和分析思路。動態規劃解最長公共子序列問題
問題描述:字元序列的子序列是指從給定字元序列中隨意地(不一定連續)去掉若干個字元(可能一個也不去掉)後所形成的字元序列。令給定的字元序列X=“x0,x1,…,xm-1”,序列Y=“y0,y1,…,yk-1”是X的子序列,存在X的一個嚴格遞增下標序列<i0,i1,…,ik-1>,使得對所有的j=0,1,…,k-1,有xij=yj。例如,X=“ABCBDAB”,Y=“BCDB”是X的一個子序列。
考慮最長公共子序列問題如何分解成子問題,設A=“a0,a1,…,am-1”,B=“b0,b1,…,bn-1”,並Z=“z0,z1,…,zk-1”為它們的最長公共子序列。不難證明有以下性質:
(1) 如果am-1=bn-1,則zk-1=am-1=bn-1,且“z0,z1,…,zk-2”是“a0,a1,…,am-2”和“b0,b1,…,bn-2”的一個最長公共子序列;
(2) 如果am-1!=bn-1,則若zk-1!=am-1,蘊涵“z0,z1,…,zk-1”是“a0,a1,…,am-2”和“b0,b1,…,bn-1”的一個最長公共子序列;
(3) 如果am-1!=bn-1,則若zk-1!=bn-1,蘊涵“z0,z1,…,zk-1”是“a0,a1,…,am-1”和“b0,b1,…,bn-2”的一個最長公共子序列。
這樣,在找A和B的公共子序列時,如有am-1=bn-1,則進一步解決一個子問題,找“a0,a1,…,am-2”和“b0,b1,…,bm-2”的一個最長公共子序列;如果am-1!=bn-1,則要解決兩個子問題,找出“a0,a1,…,am-2”和“b0,b1,…,bn-1”的一個最長公共子序列和找出“a0,a1,…,am-1”和“b0,b1,…,bn-2”的一個最長公共子序列,再取兩者中較長者作為A和B的最長公共子序列。
求解:
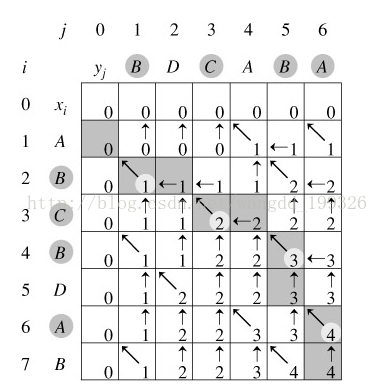
引進一個二維陣列c[][],用c[i][j]記錄X[i]與Y[j] 的LCS 的長度,b[i][j]記錄c[i][j]是通過哪一個子問題的值求得的,以決定搜尋的方向。
我們是自底向上進行遞推計算,那麼在計算c[i,j]之前,c[i-1][j-1],c[i-1][j]與c[i][j-1]均已計算出來。此時我們根據X[i] = Y[j]還是X[i] != Y[j],就可以計算出c[i][j]。
問題的遞迴式寫成:
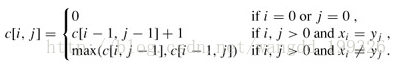
回溯輸出最長公共子序列過程:
演算法分析:
由於每次呼叫至少向上或向左(或向上向左同時)移動一步,故最多呼叫(m + n)次就會遇到i = 0或j = 0的情況,此時開始返回。返回時與遞迴呼叫時方向相反,步數相同,故演算法時間複雜度為Θ(m + n)。
#include <stdio.h>
#include <string.h>
#define MAXLEN 100
void LCSLength(char *x, char *y, int m, int n, int c[][MAXLEN], int b[][MAXLEN])
{
int i, j;
for(i = 0; i <= m; i++)
c[i][0] = 0;
for(j = 1; j <= n; j++)
c[0][j] = 0;
for(i = 1; i<= m; i++)
{
for(j = 1; j <= n; j++)
{
if(x[i-1] == y[j-1])
{
c[i][j] = c[i-1][j-1] + 1;
b[i][j] = 0;
}
else if(c[i-1][j] >= c[i][j-1])
{
c[i][j] = c[i-1][j];
b[i][j] = 1;
}
else
{
c[i][j] = c[i][j-1];
b[i][j] = -1;
}
}
}
}
void PrintLCS(int b[][MAXLEN], char *x, int i, int j)
{
if(i == 0 || j == 0)
return;
if(b[i][j] == 0)
{
PrintLCS(b, x, i-1, j-1);
printf("%c ", x[i-1]);
}
else if(b[i][j] == 1)
PrintLCS(b, x, i-1, j);
else
PrintLCS(b, x, i, j-1);
}
int main(int argc, char **argv)
{
char x[MAXLEN] = {"ABCBDAB"};
char y[MAXLEN] = {"BDCABA"};
int b[MAXLEN][MAXLEN];
int c[MAXLEN][MAXLEN];
int m, n;
m = strlen(x);
n = strlen(y);
LCSLength(x, y, m, n, c, b);
PrintLCS(b, x, m, n);
return 0;
}此處也推薦如下的幾個部落格關於對“最長公共子序列”的解法,思路與上述一樣,但是具體演算法實現上稍有不同。
4 對於“最長公共子串”的求解分析思路,推薦如右的部落格。程式設計師面試100題之七:最長公共子字串 這是大神hackbuteer1所撰寫的兩種思路,非常非常好!推薦看原部落格。關於上述3種問題的關鍵部分,我已經基本總結好,需要的同學可以再點選連結進去詳細查閱。對於該大神講解“最長公共子序列”也可以觀摩,學習。程式設計師面試100題之六:最長公共子序列
方法一:
Longest Common Substring和Longest Common Subsequence是有區別的
X = <a, b, c, f, b, c>
Y = <a, b, f, c, a, b>
X和Y的Longest Common Sequence為<a, b, c, b>,長度為4
X和Y的Longest Common Substring為 <a, b>長度為2
其實Substring問題是Subsequence問題的特殊情況,也是要找兩個遞增的下標序列
<i1, i2, ...ik> 和 <j1, j2, ..., jk>使
xi1 == yj1
xi2 == yj2
......
xik == yjk
與Subsequence問題不同的是,Substring問題不光要求下標序列是遞增的,還要求每次
遞增的增量為1, 即兩個下標序列為:
<i, i+1, i+2, ..., i+k-1> 和 <j, j+1, j+2, ..., j+k-1>
類比Subquence問題的動態規劃解法,Substring也可以用動態規劃解決,令
c[i][j]表示Xi和Yi的最大Substring的長度,比如
X = <y, e, d, f>
Y = <y, e, k, f>
c[1][1] = 1
c[2][2] = 2
c[3][3] = 0
c[4][4] = 1
動態轉移方程為:
如果xi == yj, 則 c[i][j] = c[i-1][j-1]+1
如果xi ! = yj, 那麼c[i][j] = 0
最後求Longest Common Substring的長度等於
max{ c[i][j], 1<=i<=n, 1<=j<=m}
/**
找出兩個字串的最長公共連續子串的長度
** author :liuzhiwei
** data :2011-08-16
**/
#include "stdio.h"
#include "string.h"
#include "stdlib.h"
int longest_common_substring(char *str1, char *str2)
{
int i,j,k,len1,len2,max,x,y;
len1 = strlen(str1);
len2 = strlen(str2);
int **c = new int*[len1+1];
for(i = 0; i < len1+1; i++)
c[i] = new int[len2+1];
for(i = 0; i < len1+1; i++)
c[i][0]=0; //第0列都初始化為0
for(j = 0; j < len2+1; j++)
c[0][j]=0; //第0行都初始化為0
max = -1;
for(i = 1 ; i < len1+1 ; i++)
{
for(j = 1; j < len2+1; j++)
{
if(str1[i-1]==str2[j-1]) //只需要跟左上方的c[i-1][j-1]比較就可以了
c[i][j]=c[i-1][j-1]+1;
else //不連續的時候還要跟左邊的c[i][j-1]、上邊的c[i-1][j]值比較,這裡不需要
c[i][j]=0;
if(c[i][j]>max)
{
max=c[i][j];
x=i;
y=j;
}
}
}
//輸出公共子串
char s[1000];
k=max;
i=x-1,j=y-1;
s[k--]='\0';
while(i>=0 && j>=0)
{
if(str1[i]==str2[j])
{
s[k--]=str1[i];
i--;
j--;
}
else //只要有一個不相等,就說明相等的公共字元斷了,不連續了
break;
}
printf("最長公共子串為:");
puts(s);
for(i = 0; i < len1+1; i++) //釋放動態申請的二維陣列
delete[] c[i];
delete[] c;
return max;
}
int main(void)
{
char str1[1000],str2[1000];
printf("請輸入第一個字串:");
gets(str1);
printf("請輸入第二個字串:");
gets(str2);
int len = longest_common_substring(str1, str2);
printf("最長公共連續子串的長度為:%d\n",len);
system("pause");
return 0;
}方法二:
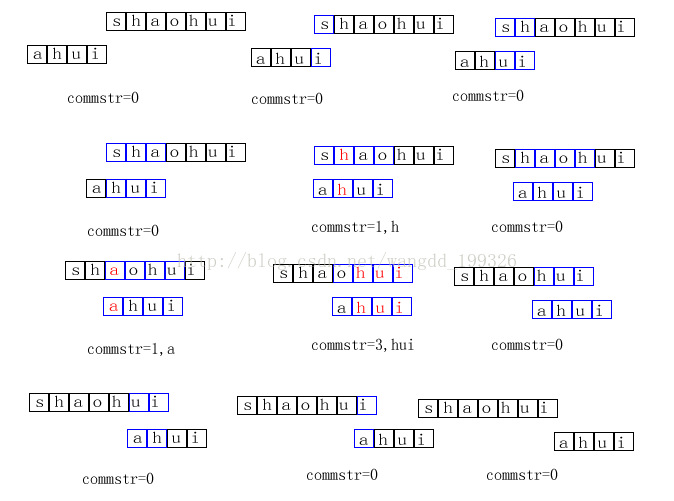
將字串s1和s2分別寫在兩把直尺上面(我依然用s1,s2來表示這兩把直尺),然後將s1固定,s2的頭部和s1的尾部對齊,然後逐漸移動直尺s2,比較重疊部分的字串中的公共子串的長度,直到直尺s2移動到s1的頭部。在這個過程中求得的最大長度就是s1、s2最大子串的長度。
下圖是求解過程的圖示(下圖有點錯誤,應該是將s2從右往左移動),藍色部分表示重疊的字串,紅色的部分表示重疊部分相同的子串
其中s1="shaohui",s2="ahui",最後求得的結果為3
/**
找出兩個字串的最長公共連續子串的長度
** author :liuzhiwei
** data :2011-08-16
**/
#include "stdio.h"
#include "string.h"
#include "stdlib.h"
int longest_common_substring(char *str1, char *str2)
{
int i,len1,len2,len,s1_start,s2_start,idx,curmax,max;
len1 = strlen(str1);
len2 = strlen(str2);
len = len1 + len2;
max = 0;
for(i = 0 ; i < len ; i++)
{
s1_start = s2_start = 0;
if(i < len1)
s1_start = len1 - i; //每次開始匹配的起始位置
else
s2_start = i - len1;
curmax = 0;
for(idx = 0 ; ( s1_start + idx < len1 ) && ( s2_start + idx < len2 ); idx++ )
{
if(str1[s1_start+idx]==str2[s2_start+idx])
curmax++;
else //只要有一個不相等,就說明相等的公共字元斷了,不連續了,要儲存curmax與max中的最大值,並將curmax重置為0
{
max = curmax > max ? curmax : max;
curmax = 0;
}
}
max = curmax > max ? curmax : max;
}
return max;
}
int main(void)
{
char str1[1000],str2[1000];
printf("請輸入第一個字串:");
gets(str1);
printf("請輸入第二個字串:");
gets(str2);
int len = longest_common_substring(str1, str2);
printf("最長公共連續子串的長度為:%d\n",len);
system("pause");
return 0;
}稍微改動一下,便可以輸出公共子串了,就是要儲存一下連續公共子串最後一個字元在其中一個字串中的下標位置:
/**
找出兩個字串的最長公共連續子串的長度
** author :liuzhiwei
** data :2011-08-16
**/
#include "stdio.h"
#include "string.h"
#include "stdlib.h"
int longest_common_substring(char *str1, char *str2)
{
int i,k,len1,len2,len,s1_start,s2_start,idx,curmax,max;
len1 = strlen(str1);
len2 = strlen(str2);
len = len1 + len2;
max = 0;
for(i = 0 ; i < len ; i++)
{
s1_start = s2_start = 0;
if(i < len1)
s1_start = len1 - i; //每次開始匹配的起始位置
else
s2_start = i - len1;
curmax = 0;
for(idx = 0 ; ( s1_start + idx < len1 ) && ( s2_start + idx < len2 ); idx++ )
{
if(str1[s1_start+idx]==str2[s2_start+idx])
curmax++;
else //只要有一個不相等,就說明相等的公共字元斷了,不連續了,要儲存curmax與max中的最大值,並將curmax重置為0
{
//max = curmax > max ? curmax : max;
if(curmax > max)
{
max = curmax;
k = s1_start+idx-1; //儲存連續子串長度增加時連續子串最後一個字元在str1字串中的下標位置,便於輸出公共連續子串
}
curmax = 0;
}
}
//max = curmax > max ? curmax : max;
if(curmax > max)
{
max = curmax;
k = s1_start+idx-1;
}
}
//輸出公共子串
char s[1000];
for(i=0;i<max;i++)
s[i]=str1[k-max+1+i]; //公共字串在str1中的下標起始位置為k-max+1,結束位置為k
s[i]='\0';
printf("最長公共子串為:");
puts(s);
return max;
}
int main(void)
{
char str1[1000],str2[1000];
printf("請輸入第一個字串:");
gets(str1);
printf("請輸入第二個字串:");
gets(str2);
int len = longest_common_substring(str1, str2);
printf("最長公共連續子串的長度為:%d\n",len);
system("pause");
return 0;
}也有其他的一些部落格,顯然沒有上述hack大神的思路詳細又好,當然可以幫助我們來學習與理解。