Combination Sum 系列問題(leetcode dfs回溯,動歸)由淺入深DFS
Combination Sum問題 在leetcode的有一系列題目
採用dfs 回溯的方法求解,當然程式碼仍需優化,剪枝是個重點
需要仔細弄懂最初的第一題,後面的就是各種調整了
39 Combination Sum(https://leetcode.com/problems/combination-sum/)
39. Combination Sum
Given a set of candidate numbers (C) and a target number (T), find all unique combinations in C where the candidate numbers sums to T.
The same repeated number may be chosen from C unlimited number of times.
Note:
All numbers (including target) will be positive integers.
The solution set must not contain duplicate combinations.
For example, given candidate set [2, 3, 6, 7] and target 7,
A solution set is:
[
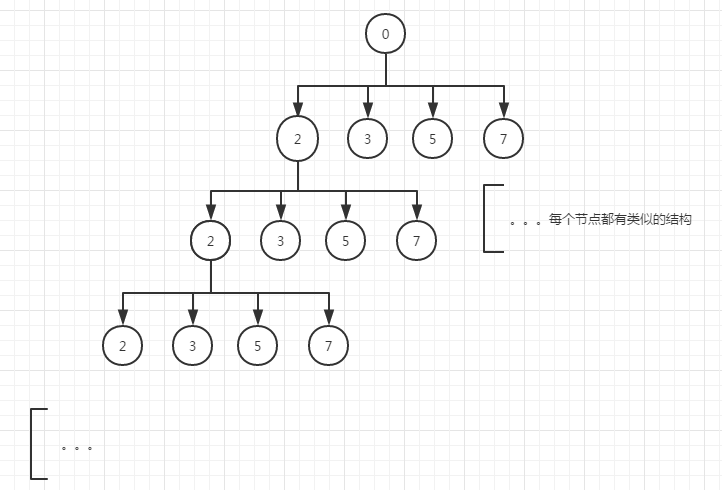
[7 此題的搜尋樹如下
第一次, 按照普通的dfs,debug發現有重複的結果
class Solution {
private:
vector<vector<int>> ans;
vector<int> rs;
public:
void dfs(int nowSum, vector<int> cand, int candSize, int target)
{
if (nowSum > target)
return 第二次,去除重複結果
//加一個nowIndex,每次只從當前到陣列末尾,不選擇比當前小的值,避免重複
class Solution {
private:
vector<vector<int>> ans;
vector<int> rs;
public:
void dfs(int nowIndex,int nowSum, vector<int> cand, int candSize, int target)
{
if (nowSum > target)
return;
if (nowSum == target)
{
ans.push_back(rs);
return;
}
for (int i = nowIndex; i < candSize; i++){
rs.push_back(cand[i]);
dfs(i,nowSum + cand[i], cand, candSize,target);
rs.pop_back();
}
}
vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
int len = candidates.size();
if (len == 0)
return ans;
sort(candidates.begin(), candidates.end());// 排序
dfs(0,0, candidates,len, target);
return ans;
}
};ac,上面在計算結果 太耗時,因為有大量的沒必要的計算
此題最終的ac程式碼
class Solution {
private:
vector<vector<int>> ans;
vector<int> rs;
public:
void dfs(int nowIndex,int nowSum, vector<int> cand, int candSize, int target)
{
if (nowSum > target)
return;
if (nowSum == target)
{
ans.push_back(rs);
return;
}
for (int i = nowIndex; i < candSize; i++){
if (nowSum + cand[i] <= target) // 因為cand是排序好的,顯然會有大量的重複,應該避免,相當於剪枝
{
rs.push_back(cand[i]);
dfs(i, nowSum + cand[i], cand, candSize, target);
rs.pop_back();// 回溯
}
else
continue;
}
}
vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
int len = candidates.size();
if (len == 0)
return ans;
sort(candidates.begin(), candidates.end());// 排序
dfs(0,0, candidates,len, target);
return ans;
}
};40. Combination Sum II
有重複結果的程式碼1
class Solution {
public:
vector<int> candi;
int candiLen;
int tar;
vector<vector<int>> rs;
vector<int> ans;
void dfs(int curIndex, int curSum)
{
if(curSum == tar)
{
for(int i=0;i<(int)ans.size();i++)
cout << ans[i] << " ";
cout << endl;
rs.push_back(ans);
return;
}
if(curIndex >= candiLen || curSum > tar)
return;
for(int i = curIndex; i < candiLen; i++)
{
if(candi[i] > tar || candi[i] + curSum > tar)
break;
ans.push_back(candi[i]);
dfs(i + 1, curSum + candi[i]);
ans.pop_back();
}
}
vector<vector<int>> combinationSum2(vector<int>& candidates, int target)
{
candi = candidates;
candiLen = candi.size();
if(candiLen > 1)
sort(candi.begin(), candi.end());
tar = target;
ans.clear();
rs.clear();
dfs(0,0);
return rs;
}
};在dfs之前,資料是排好序的,但是會有連續相同數字出現的情況,計算是會有重複的???
上面的去重條件加上 就可以ac了
class Solution {
public:
vector<int> candi;
int candiLen;
int tar;
vector<vector<int>> rs;
vector<int> ans;
void dfs(int curIndex, int curSum)
{
if(curSum == tar)
{
for(int i=0;i<(int)ans.size();i++)
cout << ans[i] << " ";
cout << endl;
rs.push_back(ans);
return;
}
if(curIndex >= candiLen || curSum > tar)
return;
for(int i = curIndex; i < candiLen; i++)
{
if(candi[i] > tar || candi[i] + curSum > tar)
break;
if(i > curIndex && candi[i] == candi[i-1]) // 去重
continue;
ans.push_back(candi[i]);
dfs(i + 1, curSum + candi[i]);
ans.pop_back();
}
}
vector<vector<int>> combinationSum2(vector<int>& candidates, int target)
{
candi = candidates;
candiLen = candi.size();
if(candiLen > 1)
sort(candi.begin(), candi.end());
tar = target;
ans.clear();
rs.clear();
dfs(0,0);
return rs;
}
};注意一個問題: 下面的兩個if在程式碼中的順序不要顛倒, why?
if(curSum == tar)
{
for(int i=0;i<(int)ans.size();i++)
cout << ans[i] << " ";
cout << endl;
rs.push_back(ans);
return;
}
if(curIndex >= candiLen || curSum > tar)
return;去重條件就一個if, why
ac2
在上一題的基礎上,保證陣列中的每個數字不能夠重複計算,所以需要設計去重的功能,在dfs時做了修改,發現仍然重複,所以有用到了c++stl map結構去重
最終的ac程式碼:
class Solution {
private:
map<vector<int>, int> mp;
vector<vector<int>> ans;
vector<int> rs;
public:
void dfs(int nowIndex,int nowSum, vector<int> cand, int candSize, int target)
{
if (nowSum > target)
return;
if (nowSum == target)
{
// 因為仍然會有重複,利用map/set去重
if (mp[rs] == 0)
{
ans.push_back(rs);
mp[rs] = 1;
}
return;
}
// 從當前的下一個開始,不包括自己,因為每個陣列中的數字
for (int i = nowIndex + 1; i < candSize; i++){
if (nowSum + cand[i] <= target) // 因為cand是排序好的,顯然會有大量的重複,應該避免,相當於剪枝
{
rs.push_back(cand[i]);
dfs(i, nowSum + cand[i], cand, candSize, target);
rs.pop_back();// 回溯
}
else
continue;
}
}
vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {
int len = candidates.size();
if (len == 0)
return ans;
sort(candidates.begin(), candidates.end());// 排序
dfs(-1,0, candidates,len, target);
return ans;
}
};
216. Combination Sum III
有了上面兩題的求解思路和基礎,這題基本上就是個自我變化的過程。不過若一開始就給出這題,應該也能想到類似的方法
ac程式碼
class Solution {
private:
vector<vector<int>> ans;
vector<int> rs;
public:
void dfs(int nowIndex,int nowSum, vector<int> cand, int candSize, int target,int nowRsSize,int k)
{
if (nowSum > target || nowRsSize > k)
return;
if (nowSum < target && nowRsSize == k)
return;
if (nowSum == target && nowRsSize == k)
{
ans.push_back(rs);
return;
}
// 從當前的下一個開始,不包括自己,因為每個陣列中的數字
for (int i = nowIndex + 1; i < candSize; i++){
if (nowSum + cand[i] <= target && nowRsSize <= k) // 因為cand是排序好的,顯然會有大量的重複,應該避免,相當於剪枝
{
rs.push_back(cand[i]);
dfs(i, nowSum + cand[i], cand, candSize, target,nowRsSize+1,k);
rs.pop_back();// 回溯
}
else
continue;
}
}
vector<vector<int>> combinationSum3(int k, int n) {
vector<int> candidates{ 1, 2, 3, 4, 5, 6, 7, 8, 9 };
dfs(-1,0, candidates,9, n,0,k);
return ans;
}
};77. Combinations
題目地址
題目描述
Given two integers n and k, return all possible combinations of k numbers out of 1 … n.
For example,
If n = 4 and k = 2, a solution is:
[
[2,4],
[3,4],
[2,3],
[1,2],
[1,3],
[1,4],
]求解
採用遞迴方式求解,因為數字不會重複,長度也限定了,思路同前面幾題
ac程式碼如下
class Solution {
private:
vector< vector<int> >ans;
vector<int> v;
public:
void dfs(int n, int k, int nowK, int indexN)
{
if (nowK > k)
return;
if (nowK == k)
{
/*for (int i = 0; i < k; i++)
cout << v[i] << " ";
cout << endl;*/
ans.push_back(v);
return;
}
for (int i = indexN; i <= n; i++)
{
v.push_back(i);
dfs(n, k, nowK + 1, i + 1);
v.pop_back();
}
}
vector<vector<int>> combine(int n, int k) {
dfs(n, k, 0, 1);
return ans;
}
};377. Combination Sum IV
題目地址
題目描述
Given an integer array with all positive numbers and no duplicates, find the number of possible combinations that add up to a positive integer target.
Example:
nums = [1, 2, 3]
target = 4
The possible combination ways are:
(1, 1, 1, 1)
(1, 1, 2)
(1, 2, 1)
(1, 3)
(2, 1, 1)
(2, 2)
(3, 1)
Note that different sequences are counted as different combinations.
Therefore the output is 7.Follow up:
What if negative numbers are allowed in the given array?
How does it change the problem?
What limitation we need to add to the question to allow negative numbers?
求解
採用dfs會超時,此題結果是很大的,因為數字可以重複,任意組合
應採用動態規劃的方法
class Solution {
public:
int combinationSum4(vector<int>& nums, int target) {
int len = nums.size();
sort(nums.begin(), nums.end());
vector<int> dp(target + 1, 0); // dp[i] 表示 能組成 等於i的個數 dp[i - num] + num 可以湊成 dp[i]
dp[0] = 1;
for (int i = 1; i <= target; i++)
{
for (int j = 0; j < len; j++)
{
if (nums[j] <= i)
dp[i] += dp[i - nums[j]];
else
break;
}
}
return dp[target];
}
};