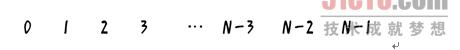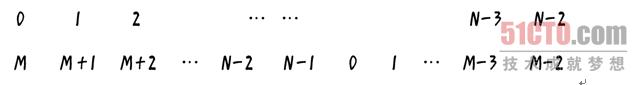5.5.4 用數學方法解約瑟夫環（1）

原文copy:http://book.51cto.com/art/201403/433941.htm

5.5.4  用數學方法解約瑟夫環（1）

上面編寫的解約瑟夫環的程式模擬了整個報數的過程，程式執行時間還可以接受，很快就可以出計算結果。可是，當參與的總人數N及出列值M非常大時，其運算速度就慢下來。例如，當N的值有上百萬，M的值為幾萬時，到最後雖然只剩2個人，也需要迴圈幾萬次（M的數量）才能確定2個人中下一個出列的序號。顯然，在這個程式的執行過程中，很多步驟都是進行重複無用的迴圈。

那麼，能不能設計出更有效率的程式呢？

辦法當然有。其中，在約瑟夫環中，只是需要求出最後的一個出列者最初的序號，而不必要去模擬整個報數的過程。因此，為了追求效率，可以考慮從數學角度進行推算，找出規律然後再編寫程式即可。

為了討論方便，先根據原意將問題用數學語言進行描述。

問題：將編號為0～（N–1）這N個人進行圓形排列，按順時針從0開始報數，報到M–1的人退出圓形佇列，剩下的人繼續從0開始報數，不斷重複。求最後出列者最初在圓形佇列中的編號。

下面首先列出0～（N–1）這N個人的原始編號如下：

根據前面曾經推導的過程可知，第一個出列人的編號一定是（M–1）%n。例如，在41個人中，若報到3的人出列，則第一個出列人的編號一定是（3–1）%41=2，注意這裡的編號是從0開始的，因此編號2實際對應以1為起點中的編號3。根據前面的描述，m的前一個元素（M–1）已經出列，則出列1人後的列表如下：

根據規則，當有人出列之後，下一個位置的人又從0開始報數，則以上列表可調整為以下形式（即以M位置開始，N–1之後再接上0、1、2……，形成環狀）：

按上面排列的順序重新進行編號，可得到下面的對應關係：
 

即，將出列1人後的資料重新組織成了0～（N–2）共N–1個人的列表，繼續求n–1個參與人員，按報數到M–1即出列，求解最後一個出列者最初在圓形佇列中的編號。

看出什麼規律沒有？對了，通過一次處理，將問題的規模縮小了。即，對於N個人報數的問題，可以分解為先求解（N–1）個人報數的子問題；而對於（N–1）個人報數的子問題，又可分解為先求[（N–1）–1]人個報數的子問題，……。

問題中的規模最小時是什麼情況？就是隻有1個人時（N=1），報數到（M–1）的人出列，這時最後出列的是誰？當然只有編號為0這個人。因此，可設有以下函式：
 

那麼，當N=2，報數到（M–1）的人出列，最後出列的人是誰？應該是隻有一個人報數時得到的最後出列的序號加上M，因為報到M-1的人已出列，只有2個人，則另一個出列的就是最後出列者，可用公式表示為以下形式：
 

通過上面的算式計算時，F(2)的結果可能會超過N值（人數的總數）。例如，設N=2，M=3（即2個人，報數到2時就出列），則按上式計算得到的值是：
 

一共只有2人蔘與，編號為3的人顯然沒有。怎麼辦？由於是環狀報數，因此當兩個人報完數之後，又從編號為0的人開始接著報數。根據這個原理，即可對求得的值與總人數N進行模運算，即：
 

5.5.4  用數學方法解約瑟夫環（2）

即，N=2，M=3（即有2個人，報數到3–1的人出列）時，迴圈報數最後一個出列的人的編號為1（編號從0開始）。我們來推算一下，如下所示，當編號為0、1的兩個人迴圈報數時，編號為0的人報的數為0和2，當報到2（M–1）時，編號0出列，最後剩下編號為1的人，所以編號為1的人最後出列。

根據上面的推導過程，可以很容易推匯出，當N=3時的公式：

同理，也可以推匯出參與人數為N時，最後出列人員編號的公式：

其實，這就是一個遞推公式，公式包含以下兩個式子：

有了這個遞推公式，再來設計程式就很簡單了，可以用遞迴的方法來設計程式，具體程式碼如下：
 

1. #include <stdio.h>
2. int main(void)  
3. {  
4.     int n,m,i,s=0;  
5.     printf ("輸入參與人數N和出列位置M的值 = ");  
6.     scanf("%d%d",&n,&m);  
7.     printf ("最後出列的人最初位置是 %d\n",josephus(n,m));  
8.     getch();  
9.     return 0 ;  
10. }  
11. int josephus(int n,int m)  
12. {  
13.     if(n==1)  
14.         return 0;  
15.     else  
16.         return (josephus(n-1,m)+m)%n;  
17. }  

在以上程式碼中，定義了一個遞迴函式josephus()，然後在主函式中呼叫這個函式進行   運算。

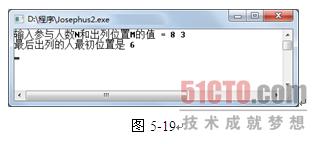
編譯執行以上程式，輸入N和M的值，可以很快得到最後出列人的編號，輸入N=8，M=3，得到的結果如圖5-19所示（注意編號是從0開始）。
 

使用遞迴函式會佔用計算機較多的記憶體，當遞迴層次太深時可能導致程式不能執行，因此，也可以將程式直接編寫為以下的遞推形式：
 

1. #include <stdio.h>
2. int main(void)  
3. {  
4.     int n,m,i,s=0;  
5.     printf ("輸入參與人數N和出列位置M的值 = ");  
6.     scanf("%d%d",&n,&m);  
7.     for (i=2; i<=n; i++)  
8. s=(s+m)%i;  
9.     printf ("最後出列的人最初位置是 %d\n",s);  
10.     getch();  
11.     return 0 ;  
12. }  

這段程式碼執行的結果與遞迴程式執行結果完全相同。

可以看出，經過一些數學推導，最後總結出規律簡化程式，將幾十行的程式碼縮減到幾行。更主要的是，程式執行的效率得到大大的提升，省去了很多重複的迴圈，既使求解的N和M值很大，也不會成為問題