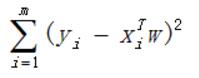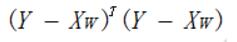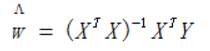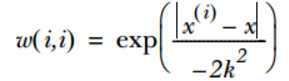迴歸:最佳擬合直線與區域性線性迴歸
- 迴歸是用來做什麼的?
迴歸可以做任何事,例如銷售量預測或者製造缺陷預測。
- 什麼是迴歸?
迴歸有線性迴歸和非線性迴歸,本篇文章主要討論線性迴歸。迴歸的目的是預測數值型的目標值。最直接的辦法是依據輸入寫出一個目標值的計算公式,即所謂的迴歸方程,可表示為:
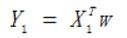
具體的做法是用迴歸係數乘以輸入值,再將結果全部加在一起,就得到了預測值。其中,求迴歸係數的過程就是迴歸,一旦有了迴歸係數,再給定輸入,做預測就很容易了。
- 迴歸的一般方法:
1. 收集資料
2. 準備資料
3. 分析資料
4. 訓練演算法:找到迴歸係數
5. 測試演算法:可使用預測值和資料的擬合度,來分析模型的效果
6. 使用演算法:使用迴歸,可在給定輸入的時候預測出一個數值
一、用線性迴歸找到最佳擬合直線
怎樣求出迴歸方程?假設手裡有一些X和對應的Y,怎樣才能找到迴歸係數w呢?一個常用的方法就是找出使預測值和實際值誤差最小的w。這裡的誤差即預測y值和實際y值之間的差值,即 y-wx ,但若使用該誤差的簡單累加將使得正差值和負差值相互抵消,所以在此我們採用平方誤差,計算所有點的平方誤差之和,即:
用矩陣表示還可以寫做:
如果對w求導,便可得到: 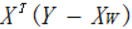
令其等於0,解出w如下:
(上述過程可由最小二乘法解出)
從現有資料上估計出的w可能並不是資料中的真是w值,w上方的小標記表示它僅是w的一個最佳估計。
上述公式中包含求逆矩陣,因此此方程僅在逆矩陣存在時使用。逆矩陣可能並不存在,因此需要在程式碼中做出判斷。
具體執行程式碼如下:
1.匯入需要使用的庫:
from numpy import *
import numpy as np2.讀取資料:
def loadDataSet(fileName): numFeat = len(open(fileName).readline().split('\t')) - 1 print(numFeat) dataMat = []; labelMat = [] fr = open(fileName) for line in fr.readlines(): lineArr = [] curLine = line.strip().split('\t') for i in range(numFeat): lineArr.append(float(curLine[i])) dataMat.append(lineArr) labelMat.append(float(curLine[-1])) return dataMat,labelMat
3.計算迴歸係數:
def standRegres(xArr, yArr):
xMat = mat(xArr); yMat = mat(yArr).T
xTx = xMat.T*xMat
if linalg.det(xTx) == 0.0:
print("This matrix is singular,cannot do inverse")
return
ws = xTx.I*(xMat.T*yMat)
return ws4.依據迴歸方程預測資料值:
xMat = mat(xArr)
yMat = mat(yArr)
yHat = xMat * ws5.計算相關係數,測試演算法:
yHat = xMat * ws
corrcoef(yHat.T,yMat)6.用matplotlib繪出圖表:
import matplotlib.pyplot as plt
fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(xMat[:,1].flatten().A[0],yMat.T[:,0].flatten().A[0])
xCopy = xMat.copy()
xCopy.sort(0)
yHat = xCopy * ws
ax.plot(xCopy[:,1],yHat)
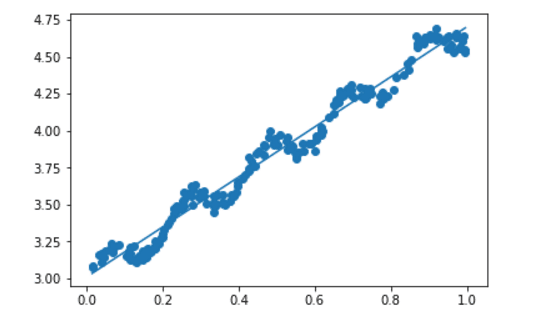
plt.show()7.最終輸出圖表:
至此,完整的最佳擬合直線線性迴歸結束。
- 優點:計算簡單,結果易於理解
- 缺點:對非線性的資料擬合不好
- 適用資料型別:數值型和標稱型資料
二、區域性加權線性迴歸
因為線性迴歸最佳擬合直線的方法求的是具有最小均方誤差的無偏估計,對於非線性資料,有可能出現欠擬合的現象,無法取得最好的預測效果,因此,允許在估計中引入一些偏差,從而降低預測的均方誤差。
其中一個方法是區域性加權線性迴歸,在該演算法中,我們給待預測點附近的每個點賦予一定的權重,然後與最佳擬合直線迴歸類似,在這個子集上基於最小均方差來進行普通的迴歸。該演算法對應的迴歸係數w的形式如下:
在此,我們使用核來對附近的點賦予更高的權重。核的型別可自由選擇,最常用的是高斯核,高斯核對應的權重如下:
這樣就構建了一個權重矩陣W,並且點 x 與 x(i) 越近,W(i,i) 越大。上述公式包含了一個需使用者指定的引數k,它決定了對附近 的點賦予多大的權重。若選取k值過大,則會導致欠擬合,k值過小則考慮了太多的噪聲,進而導致過擬合現象,在此案例中,我們選擇k=0.003。
具體的執行程式碼只需在最佳擬合直線的基礎上改用新的方法去求迴歸係數w,並且最終預測資料值:
1.定義一個函式,可求出迴歸係數與輸入資料的積:
def lwlr(testPoint , xArr , yArr ,k = 1.0):
xMat = np.mat(xArr); yMat = np.mat(yArr).T
m = np.shape(xMat)[0]
weights = np.mat(eye((m)))
for j in range(m):
diffMat = testPoint - xMat[j,:]
weights[j,j] = exp(diffMat * diffMat.T / (-2.0 * k ** 2))
xTx = xMat.T * (weights * xMat)
if linalg.det(xTx) == 0.0:
print('This matrix is singular , cannot do inverse')
return
ws = xTx.I * (xMat.T * (weights * yMat))
return testPoint * ws2.呼叫函式,預測資料值:
def lwlrTest(testArr,xArr,yArr,k = 1.0):
m = np.shape(testArr)[0]
yHat = np.zeros(m)
for i in range(m):
yHat[i] = lwlr(testArr[i],xArr,yArr,k)
return yHat3.呼叫函式,用matplotlib畫出圖表:
yHat = lwlrTest(xArr,xArr,yArr,0.003)
srtInd = xMat[:,1].argsort(0)
xSort = xMat[srtInd][:,0,:]fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(xSort[:,1],yHat[srtInd])
ax.scatter (xMat[:,1].flatten().A[0],np.mat(yArr).T.flatten().A[0],s=2,c='red')
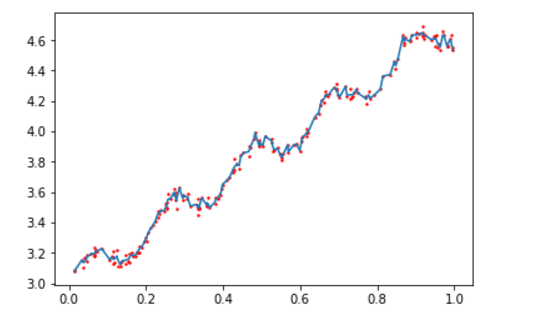
plt.show()4.最終輸出區域性加權迴歸函式圖:
區域性加權線性迴歸也存在一個問題,即增加了計算量,因為它對每個點做預測時都必須使用整個資料集。我們選取k=0.01可以得到很好的估計,但同時可以發現大多數資料點的權重都接近零。如果避免這些計算將可以減少程式執行時間,從而緩解因計算量增加帶來的問題。