2. 程式人生 > >【機器學習】筆記之聚類Cluster—— 層次聚類 Hierarchical clustering

【機器學習】筆記之聚類Cluster—— 層次聚類 Hierarchical clustering

阿新 • • 發佈：2019-02-20

什麼是層次聚類Hierarchical clustering?

平面聚類是高效且概念上簡單的，但它有許多缺點。 演算法返回平坦的非結構化簇集合，需要預先指定的簇數目作為輸入並且這個數目是不確定的。 分層聚類（或分層聚類）輸出層次結構，這種結構比平面聚類返回的非結構化聚類集更具資訊性。 分層聚類不需要我們預先指定聚類的數量，並且在IR(Information Retrieval)中使用的大多數分層演算法是確定性的。 分層聚類的這些優點以降低效率為代價。 與K-means和EM的線性複雜度相比，最常見的層次聚類演算法具有至少二次的文件數量的複雜性。

平面和層次聚類在資訊檢索中的應用差異很小。 特別是，分層聚類適用於

該文章中Table1中所示的任何應用程式。 實際上，我們為collection clustering提供的示例是分層的。 一般來說，當考慮聚類效率時，我們選擇平面聚類，當平面聚類的潛在問題（不夠結構化，預定數量的聚類，非確定性）成為關注點時，我們選擇層次聚類。 此外，許多研究人員認為，層次聚類比平面聚類產生更好的聚類。 但是，在這個問題上沒有達成共識（見第17.9節中的參考文獻）。

我們首先介紹了凝聚層次聚類（第17.1節），並在第17.2-17.4節介紹了四種不同的凝聚演算法，它們採用的不同的相似性量度：single-link, complete-link, group-average, and centroid similarity。 然後，我們將在第17.5節討論層次聚類的最優性條件。 第17.6節介紹了自上而下（divisive）的層次聚類。 第17.7節著眼於自動標記聚類，這是人類與聚類輸出互動時必須解決的問題。 我們在第17.8節討論實現問題。 第17.9節提供了進一步閱讀的指示，包括對軟分層聚類的引用，我們在本書中沒有涉及。

凝聚分層聚類(Hierarchical agglomerative clustering):

分層聚類演算法可以是自上而下的，也可以是自下而上的。 自下而上演算法在開始時將每個文件視為單個簇，然後連續地合併（或聚合）簇對，直到所有簇已合併到包含所有文件的單個簇中。 因此，自下而上的層次聚類稱為凝聚分層聚類或HAC。在介紹HAC中使用的特定相似性度量之前，我們首先介紹一種以圖形方式描述層次聚類的方法，討論HAC的一些關鍵屬性，並提出一種計算HAC的簡單演算法。

HAC聚類通常視覺化為樹狀圖(Dendrogram)，如圖1所示。 每個合併由水平線表示。 水平線的y座標是合併的兩個聚類的相似度（cosine similarity: 1為完全相似，0為完全不一樣），其中文件被視為單個聚類。 我們將這種相似性稱為合併簇的組合相似性(combination similarity)

。

\includegraphics[width=15cm]{rprojectsingle.eps}
Figure 1.  A dendrogram of a single-link clustering of 30 documents from Reuters-RCV1. 兩個可能的分割：0.4劃分成24個簇；0.1劃分成12個簇.

通過從底層向上移動到頂層節點，樹形圖允許我們重建已經合併的簇。 例如，我們看到名為War hero Colin Powell的兩個檔案首先在Figure 1中合併，並且在最後一次合併中加入了Ag trade組成了一個包含其他29個檔案組成的簇。 HAC的一個基本假設是合併操作是單調的。 單調意味著如果$s_1,s_2,\ldots,s_{K-1}$是HAC的連續合併的組合相似性，則$s_1 \geq s_2 \geq \ldots \geq s_{K-1}$成立。分層聚類不需要預先指定數量的聚類。 但是，在某些應用程式中，我們需要像平面聚類一樣對不相交的簇進行分割槽。 在這些情況下，需要在某個時刻削減層次結構。 可以使用許多標準來確定切割點：

  • 削減預先指定的相似度。 例如，如果我們想要最小組合相似度為0.4的聚類，我們將樹形圖切割為0.4。 在圖1中，以$ y = 0.4 $切割圖表產生了24個聚類（僅將具有高相似性的文件組合在一起），並將其切割為$ y = 0.1 $，產生12個聚類（一個大型財經新聞聚類和11個較小聚類）。
  • 如果兩個連續的組合相似性之間的差距最大，那麼就在此處切割樹。 如此大的差距可以說是“自然的”聚類。 再新增一個簇會顯著降低聚類的質量，因此需要在發生這種急劇下降之前進行切割。 This strategy is analogous to looking for the knee in the 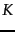$K$-means graph in Figure 16.8 (page 16.8 ).
  • 應用公式：

\begin{eqnarray*} K = \argmin_{K'} [\mbox{RSS}(K') + \lambda K'] \end{eqnarray*}

其中$ K'$指的是導致$ K'$個簇的層次結構的削減，RSS是剩餘的平方和(residual sum of squares)，$ \ lambda $是每個額外簇的懲罰。 可以使用另一種失真度量來代替RSS。

  • 與平面聚類一樣，我們也可以預先指定聚類的數量並選擇產生聚類的切割點。

一個簡單的HAC演算法如Figure 2所示。 我們首先計算$N \times N$相似度矩陣$ C $。然後該演算法執行$ N-1 $步(e.g.10個樣本需要N-1=9次來最終將所有樣本cluster到一起)來合併當前最相似的簇。 在每次迭代中，合併兩個最相似的簇(比如 $i$ 和 $m$)，將這個簇與其他簇從新計算相似度並更新到相似度矩陣$ C $中$i$的行和列。這樣做的目的是利用&i&來表示新合併好的簇。然後將$m$ deactivated，這樣做在以後的迭代中，&i&便用來代表包含&i&的簇，而$m$將不再被考慮（$m$已經被聚類）。合併形成的簇以列表的形式儲存在&A&中。$ I $表示哪些群集仍然可以合併(如前文所說的$m$，若$m$沒有被聚類則$I[m]=1$否則$I[m]=0$)。 函式SIM$(\oldell i,m,j)$計算簇$ j $與簇$ i $和$ m $合併的相似性。 對於某些HAC演算法，SIM$(\oldell i,m,j)$$C[j][i]$只是和$ C [j] [m] $的函式，例如，這兩者中的single-link的值。 

\begin{figure}\begin{algorithm}{SimpleHAC}{d_1,\ldots,d_N}\begin{FOR}{n \= 1 \......\emph{(deactivate cluster)}\end{FOR}\\\RETURN{A}\end{algorithm}\end{figure}
Figure 2. A simple, but inefficient HAC algorithm

相似性度量：Single-link and complete-link clustering：

Single-link clustering: 在single-link clustering中，兩個聚類的相似性是其最相似成員的相似性。 Single-link合併標準是本地的。 也就是說，我們只關注兩個簇彼此最接近的區域， 其他更遠的簇的整體結構不予考慮。參考Figure 2(a)。

Complete-link clustering: 在Complete-link中，兩個聚類的相似性是它們最不相似的成員的相似性。 這相當於選擇合併具有最小直徑的簇對。 Complete-link合併標準是非本地的; 簇的整個結構可以影響合併決策。 這導致Complete-link傾向於在長的，散亂的簇上選擇具有小直徑的緊密簇，但也導致對異常值的敏感性。 遠離中心的單個文件可以顯著增加候選合併叢集的直徑，並完全改變最終的叢集。參考Figure 2(b)。

Figure 2. The different notions of cluster similarity used by HAC algorithms

Figure 17.2描繪了八個文件的Single-link and Complete-link clustering。 前四個步驟，每個步驟產生一個由兩個文件組成的簇，兩種方法的結果是相同的。 然後Single-link clustering連線上面的兩對，之後是下面的兩對，因為在聚類相似性的最大相似性定義上，這兩個聚類最接近。 Complete-link clustering連線左兩對（然後是右兩對），因為根據聚類相似性的最小相似性定義，它們是最接近的對。

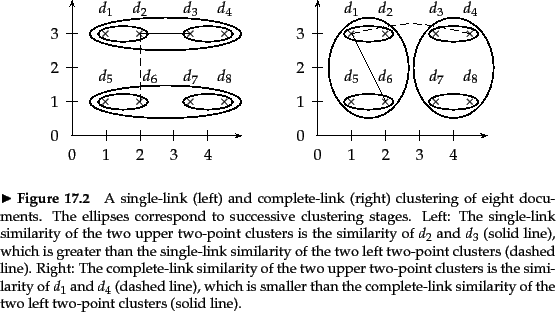
\begin{figure}% latex2html id marker 26488\par\psset{unit=0.75cm}\par\begin......e-link similarity of thetwo left two-point clusters (solid line).}\end{figure}

Figure 1是一組文件的Single-link cluster的示例，Figure 3是同一組檔案的Complete-link cluster。當切割Figure 3中的最後一個合併時，我們獲得兩個相似大小的簇。 Figure 1中的樹狀圖沒有這樣的切割可以為我們提供同樣平衡的聚類。 

\includegraphics[width=13.5cm]{rprojectcomplete.eps}
Figure 3. A dendrogram of a complete-link clustering of 30 documents from Reuters-RCV1. 

Single-link and Complete-link clustering都具有圖形理論解釋。將$ s_k $定義為合併步驟$ k $中的兩個簇的組合相似度，將$ G（s_k）$定義為已經根據相似度大於$ s_k $的相似度合併好的樹（我的理解：將$ G（s_k）$定義為截止到第$ k $步所合併形成的樹圖）。 在完成了$ k $次聚類以後，通過Single-link clustering形成的樹包含了很多connected components，而通過Complete-link形成的樹則包含了很多cliques。

Connected components：A maximal set of connected points such that there is a path connecting each pair.

Clique: A clique is a set of points that are completely linked with each other.

到這為止，我們要清楚：Single-link clustering在每一次聚類時，只要當前即將要合併的兩個簇中保證有一個樣本樣本對的相似度最大即可。而在Complete-link clustering中，即將要合併的兩個簇必須要保證所有樣本對的相似度都很小（根據兩個簇最不相似的樣本對相似最大，那麼這兩個簇中任意的兩個樣本對的相似度必都大於最不相似樣本對相似度）。就好比是一個朋友圈，這個圈子裡只要有一個人喜歡你，就把你加進來——Single-link cluster；所有人都喜歡你才能把你加進來——Complete-link clustering。

鏈式效應在Figure 1中也很明顯。 Single-link clustering的最後十一個合併（超過$ 0.1 $行的那些）新增單個文件或文件對，可看作是鏈式效應。 Figure 3中的Complete-link clustering避免了這個問題。 當我們在最後一次合併時剪下樹形圖時，文件被分成兩組大小相等的大小。 通常，我們更想得到一個平均的叢集而不是鏈式的叢集。

但是，Complete-link clustering會遇到不同的問題。 它過分關注異常值，這些點不適合叢集的全域性結構。 在Figure 4的示例中，四個文件$ d_2d_3d_4d_5 $由於左邊緣的異常值$ d_1 $而被拆分。 在此示例中，Complete-link clustering未找到最直觀的群集結構。

相關推薦

【機器學習】筆記之聚類Cluster—— 層次聚類 Hierarchical clustering

什麼是層次聚類Hierarchical clustering? 平面聚類是高效且概念上簡單的，但它有許多缺點。 演算法返回平坦的非結構化簇集合，需要預先指定的簇數目作為輸入並且這個數目是不確定的。 分層聚類（或分層聚類）輸出層次結構，這種結構比平面聚類返回的非結構化聚類

王小草【機器學習】筆記--無監督演算法之聚類

標籤（空格分隔）： 王小草機器學習筆記 1. 聚類的概述 存在大量未標註的資料集，即只有特徵，沒有標籤的資料。 根據這些特徵資料計算樣本點之間的相似性。 根據相似性將資料劃分到多個類別中。 使得，同一個類別內的資料相似度大，類別之間的資料相似度小。

【機器學習】接地氣地解釋K-means聚類演算法

       俗話說“物以類聚，人以群分”，這句話在K-means聚類演算法裡面得到了充分的繼承。而K-means演算法的實際應用範圍可謂是大到無法估量，基本可以說，只要你想不到，沒有聚類聚不起來的東西！       &nbs

【機器學習】筆記01

機器學習總體流程圖 機器學習 四個階段 1.資料預處理階段： 特徵提取：將原始資料轉化為特徵資料，從而能夠有效的對原始資料所涵蓋的資訊進行表達（raw data→feature）； 特徵選擇：有時會從原始資料提取很多的特徵，我們選擇出一部分特徵來以適應當前的

王小草【機器學習】筆記--主題模型LDA實踐與應用

標籤（空格分隔）： 王小草機器學習筆記 筆記整理時間：2016年12月30日 筆記整理者：王小草 1. LDA的實現工具 在主題模型LDA的理論篇，長篇大幅的公式與推導也許實在煩心，也不願意自己去寫程式碼實現一遍的話，不妨用一用一些已經開源和

【機器學習】筆記--梯度提升（Gradient boosting)

1 提升的概念 提升是機器學習技術，可以用於迴歸和分類問題，它每一步產生一個弱預測模型（如決策樹），並加權累加到總模型中

王小草【機器學習】筆記--EM演算法

標籤（空格分隔）： 王小草機器學習筆記 EM演算法的英文全稱是Expectation Maximization Algorithm，也就是求期望最大化，也就是我們常說的目標函式求最大值的演算法。EM演算法，直觀的說，就是有一堆未知的資料（比如一些特徵值），

王小草【機器學習】筆記--支援向量機SVM

標籤（空格分隔）： 王小草機器學習筆記 1.SVM的原理與目標 1.1 分割超平面 來看上圖，假設C和D是兩個不想交的凸集，則存在一個超平面P，這個P可以將C和D分離。 這兩個集合的距離，定義為兩個集合間元素的最短距離。 做集合C和集合

【機器學習】DBSCAN Algorithms基於密度的聚類算法

多次 使用 缺點 有效 結束 基於 需要 att 共享 一、算法思想： DBSCAN(Density-Based Spatial Clustering of Applications with Noise)是一個比較有代表性的基於密度的聚

【機器學習】---密度聚類從初識到應用

max 一個 eight log div 指定 聚類 空間 mar 一.前述 密度聚類是一種能降噪的算法。 二.相關概念 先看些抽象的概念（官方定義）： 1.：對象O的是與O為中心，為半徑的空間，參數，是用戶指定每個對象的領域半徑值。 2.MinPts（領域密度閥值）：對象

【機器學習】Kmeans聚類

寫在篇前   Kmeans演算法是一種經典的聚類演算法，屬於無監督學習的範疇。所謂聚類，即指對於給定的一個樣本集，按照樣本之間的距離大小，將樣本集劃分為K個簇，且讓簇內的點儘量緊密的連在一起，而讓簇間的距離儘量的大。 優點： 原理簡單 速度快 對大資料集有比較

【機器學習】層次聚類

寫在篇前   層次聚類（hierarchical clustering）是一種通用的聚類演算法之一，它通過自下而上合併或自上而下拆分來構建巢狀聚類。這種簇的層次結構表示為樹（或樹狀圖），樹的根匯聚所有樣本，樹的葉子是各個樣本。本篇部落格會簡述層次聚類的原理，重點

【機器學習】K-means聚類演算法初探

資料聚類是對於靜態資料分析的一門技術，在許多領域內都被廣泛地應用，包括機器學習、資料探勘、模式識別、影象分析、資訊檢索以及生物資訊等。聚類是把相似的物件通過靜態分類的方法分成不同的組別或者更多的子集，這樣讓在同一個子集中的成員物件都有相似的一些屬性，常見的包括在座標系中

【機器學習】人像識別（三）——K-Means聚類

簡介 　　K-Means聚類是一種非監督的聚類方式，原理參看資料探勘十大演算法 | k-means。 　　 程式碼 import sys import random import numpy as np from sklearn.decomposit

【機器學習】【層次聚類演算法-1】HCA(Hierarchical Clustering Alg)的原理講解 + 示例展示數學求解過程

層次聚類(Hierarchical Clustering)是聚類演算法的一種，通過計算不同類別資料點間的相似度來建立一棵有層次的巢狀聚類樹。在聚類樹中，不同類別的原始資料點是樹的最低層，樹的頂層是一個聚類的根節點。建立聚類樹有自下而上合併和自上而下分裂兩種方法，本篇文章介紹合併方法。層次聚類的合併演算法層次聚

【機器學習】聚類演算法：層次聚類

本文是“漫談 Clustering 系列”中的第 8 篇，參見本系列的其他文章。 系列不小心又拖了好久，其實正兒八經的 blog 也好久沒有寫了，因為比較忙嘛，不過覺得 Hierarchical Clustering 這個話題我能說的東西應該不多，所以還是先寫了吧（我準

【機器學習】常用聚類演算法原型

1. 聚類簡介 在機器學習中，分為監督學習、無監督學習和半監督學習。前一篇部落格中提到的迴歸和分類都屬於監督學習，本文著重探討無監督學習中的聚類演算法。 博主之前看過一些資料，這兩天也翻閱了網上的各大部落格後，也想總結一下，寫一寫聚類相關的知識點，對

【機器學習】聚類演算法：層次聚類、K-means聚類

     所謂聚類，就是將相似的事物聚集在一 起，而將不相似的事物劃分到不同的類別的過程，是資料分析之中十分重要的一種手段。比如古典生物學之中，人們通過物種的形貌特徵將其分門別類，可以說就是 一種樸素的人工聚類。如此，我們就可以將世界上紛繁複雜的資訊，簡化為少數方便人們理解的類別，可以說是人類認知這個

【機器學習】聚類

1. 距離計算   當對一些沒有 Label 的資料進行分類的時候，需要滿足一些的基本性質： 非負性：dist(xi,xj)≥0dist(xi,xj)≥0； 同一性：dist(xi,xj)=0dist(xi,xj)=0，當且僅當 xi=xjxi=xj； 對

【機器學習】：Kmeans均值聚類演算法原理(附帶Python程式碼實現)

這個演算法中文名為k均值聚類演算法，首先我們在二維的特殊條件下討論其實現的過程，方便大家理解。 第一步.隨機生成質心 由於這是一個無監督學習的演算法，因此我們首先在一個二維的座標軸下隨機給定一堆點，並隨即給定兩個質心，我們這個演算法的目的就是將這一堆點根據它們自身的座標特徵分為兩類，因此選取了兩個質心，什麼時