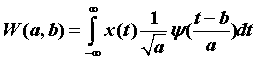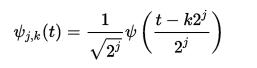為什麼會出現小波變換

視窗傅立葉變換（短時傅立葉變換）雖然可以部分定位時間，但由於視窗大小是固定的，只適用於頻率波動小的平穩訊號，不適用於頻率波動大的非平穩訊號。而小波變換可以根據頻率的高低自動調節視窗大小，是一種自適應的時頻分析方法，可以進行多解析度分析。

從連續小波變換說起

連續小波變換（Continuous Wavelet Transform，CWT）的定義如下：

這裡有兩個變數——a，b，它們分別控制小波的兩個變換。

scaling（或者叫dilation，延展）：stretching and shrinking the signal in time，完全由a控制，可以改變小波變換的中心頻率（ center frequency）

設母小波的中心頻率為Fc，那麼子小波等效的訊號頻率（pseudo-frequency，偽頻率）為：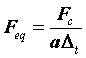
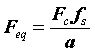
 （Fc是尺度為1的小波中心頻率，a是尺度，delta t是取樣間隔）或者寫成（fs是取樣頻率）

在matlab中cwt將訊號的取樣頻率歸一化為1了.

可見，等效頻率和尺度成反比關係。

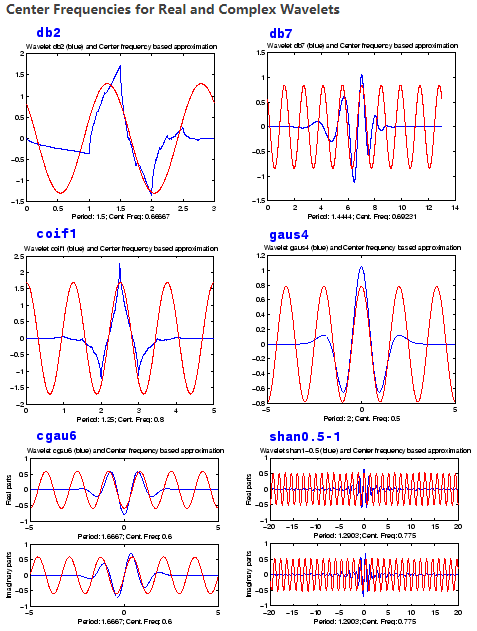
中心頻率指的是對小波進行傅立葉變換，最小的那個頻率就是這個小波的頻率，這個頻率最能代表小波中間部分的頻率和小波的能量。 the center frequency-based approximation captures the main wavelet oscillations. The center frequency is a convenient and simple characterization of the dominant frequency of the wavelet.

小波在時域上還是衰減的，且積分面積為0！

小波的中心頻率和頻寬 的計算公式如下：

以Morlet wavelet為例，我們可以得到一些重要的結論：

1.橫著看，b不影響小波頻率

2.豎著看，a=1是基小波，當a<1時，時域壓縮，頻寬增大，頻率增大；當a>1時，時域伸展，頻寬減小，頻率減小。

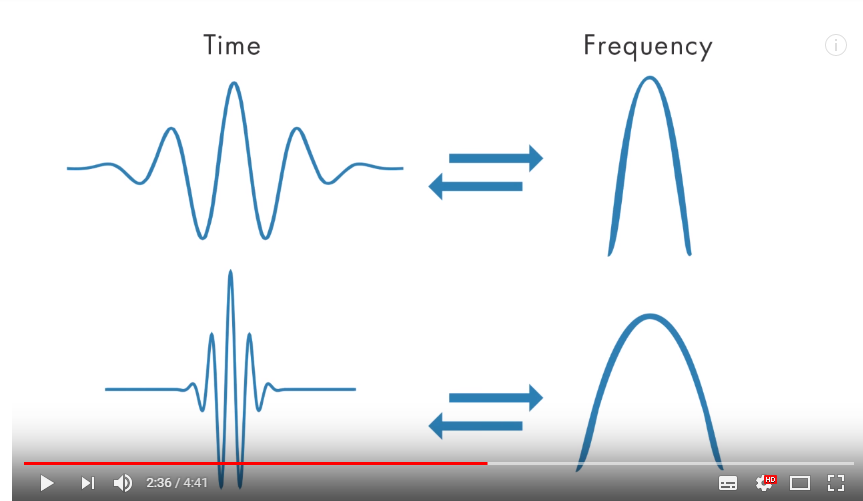
事實上，頻寬只與a有關，而且時間寬度*頻率寬度是一個常數。尺度越大，越低頻，時間解析度越高，頻率解析度越低；尺度越小，越高頻，時間解析度越低，頻率解析度越高。這一特性非常重要：

注：小波作用在訊號上，具有帶通特性：

shifting(或者叫translation，平移)：delaying or advancing the onset of the wavelet along the length of the signal，完全由b控制，控制小波基在時間軸上沿著訊號滑動

舉個例子：

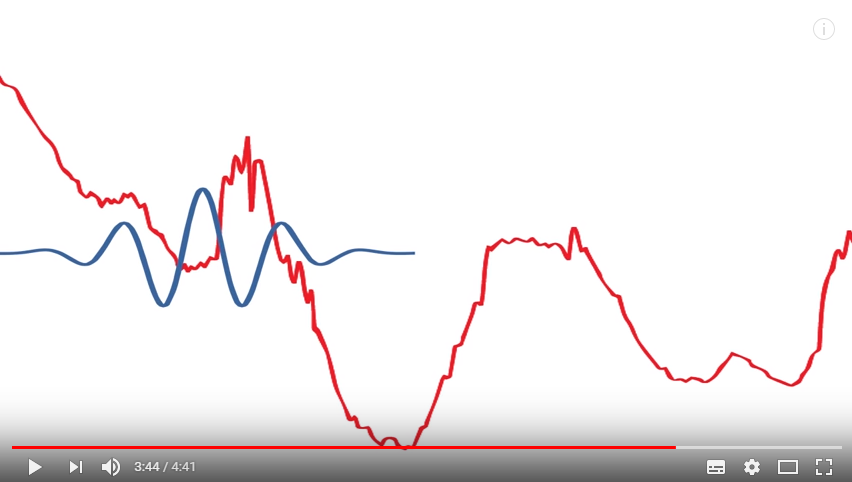
用小波刻畫下面這個時間訊號：

a stretched wavelet help capture the solely varying changes:

a compressed wavelet help capture the abrupt changes:

我們可以調整小波尺度構建出任意頻率的子小波！！

連續小波變換的主要應用如下：time frequency analysis and filtering of time localized frequency components

常用的小波有：Morse Wavelets、Bump Wavelets、Analytic Morlet Wavelet

在實際應用時，將尺度以2為基底取樣：

一般每一組的尺度個數選擇：10 、12、16、32

將不同尺度的小波沿著訊號移動，與訊號比較得到一系列coefficients。例如1000 samples X 20 scales = 20,000 coefficients，以此刻畫隨時間振盪的訊號

回到離散小波變換

離散小波變換（Discrete Wavelet Transform，DWT）定義如下，對連續小波的尺度和平移引數取樣，一般是以2為底進行取樣：

，

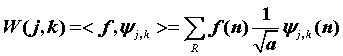
主要應用有：denoising and compression of signals and images 

由於內積運算太複雜，所以試圖去找快速演算法。

第一代小波：Mallat分解 1987

採用低通濾波器h(n)和高通濾波器g(n)，在行方向對影象濾波，並進行下2 取樣；再在列方向濾波並進行下2 取樣，可以進一步對低頻部分進行多級小波金字塔分解。

First the samples are passed through a low pass filter with impulse response  g resulting in a convolution of the two.The signal is also decomposed simultaneously using a high-pass filter h. The outputs giving the detail coefficients (from the high-pass filter) and approximation coefficients (from the low-pass). It is important that the two filters are related to each other and they are known as a quadrature mirror filter.(正交映象)

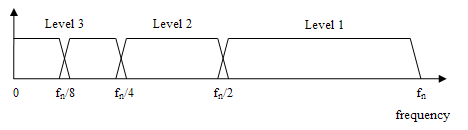
多次進行低通，高通濾波及將取樣，可以得到如下濾波器組：

下面是3級變換後得到的4個輸出的頻率範圍示意圖：

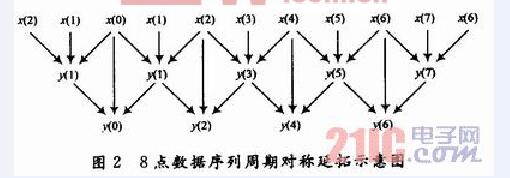
分解後的序列是原序列與濾波器序列的卷積再進行隔點抽取而來。即分解抽取的結果長度為(srcLen+filterLen-1)/2。

分解與重構：

分解和重構濾波器的關係：

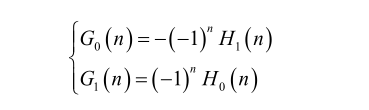
計算時邊緣是要補0的，有如下方法：
1）零值填補
0 , -(filterLen -1)≤ n< 0
f′(n)= f(n) , 0≤ n≤srcLen -1
0 , srcLen -1< n≤srcLen+filterLen -2
舉例說明：以“1 2 3 4 5 6 7 8”這個長度為8的訊號為例，當濾波器的長度為4時，其具體的拓延長度為6（單邊為3）：0 0 0 （1 2 3 4 5 6 7 8）0 0 0

2）週期拓延：
f(n+ srcLen) , -(filterLen -1)≤ n< 0
f′(n)= f(n) , 0≤ n≤ srcLen -1
f(n -srcLen) , srcLen -1< n≤srcLen+filterLen -2
舉例說明：以“1 2 3 4 5 6 7 8”這個長度為8的訊號為例，當濾波器的長度為4時，其具體的拓延長度為6（單邊為3）：6 7 8 （1 2 3 4 5 6 7 8）1 2 3

3）對稱延拓（重點）
f(-n -1) , -(filterLen-1)≤ n< 0
f′(n)= f(n) , 0≤ n≤srcLen-1
f(2srcLen -n -1) , srcLen-1< n≤ srcLen+ filterLen-2
舉例說明：以“1 2 3 4 5 6 7 8”這個長度為8的訊號為例，當濾波器的長度為4時，其具體的拓延長度為6（單邊為3）：3 2 1 （1 2 3 4 5 6 7 8）8 7 6

一個例項：

Mallat演算法是基於卷積的，計算複雜度較高，儲存空間要求較高。

第二代小波，提升格式（Sweldens和Daubechies等）1995

（1）分解。將輸入訊號s(i)分為2個較小的子集s(i-1)和d(i-1)。最簡單的分解方法是按奇偶分為2 組，這種分裂所產生的小波稱為懶小波（lazy wavelet）。
（2）預測。在基於原始資料相關性的基礎上，用偶數序列s(i-1)的預測值P(s(i-1))去預測（或者內插）奇數序列d(i-1)，即將濾波器P對偶數訊號作用以後作為奇數訊號的預測值，奇數訊號的實際值與預測值相減得到殘差訊號。實際中雖然不能從子集s(i-1)中準確地預測子集d(i-1)，但是P(s(i-1))有可能很接近d(i-1)，因此我們可以使用P(s(i-1))和d(i-1)的差值來代替原來的d(i-1)，這樣產生的d(i-1)比原來的 d(i-1)包含更少的資訊，於是得到d(i-1)=d(i-1)-P(s(i-1))，這裡，已經可以用更小的子集s(i-1)和子集d(i-1)來代替原訊號集s(i)。重複分解和預測過程，經過n步以後原訊號集可用{s(n),d(n),s(n-1),d(n-2),.....,d(1)}來表示。
（3）更新。為 了使原始訊號集的某些全域性特性在其子集s(i-1)中繼續保持，使得它保持原圖的某一標量特性Q(x)（如均值、消失矩等不變），即有Q(s(i-1))=Q(s(i))。可能利用已經計算的小波子集d(i-1)對s(i-1)進行更新，從而使得後者保持特性Q(x)，即要構造一個運算元U去更新 s(i-1)。定義如下：
s(i-1)=s(i-1)+U(d(i-1))
從上述分析可以知道，提升方法可以實現原位運算，即該方法不需要除了前級提升步驟的輸出之外的資料，這樣在每個點都可以運用新的資料流替換舊的資料流。

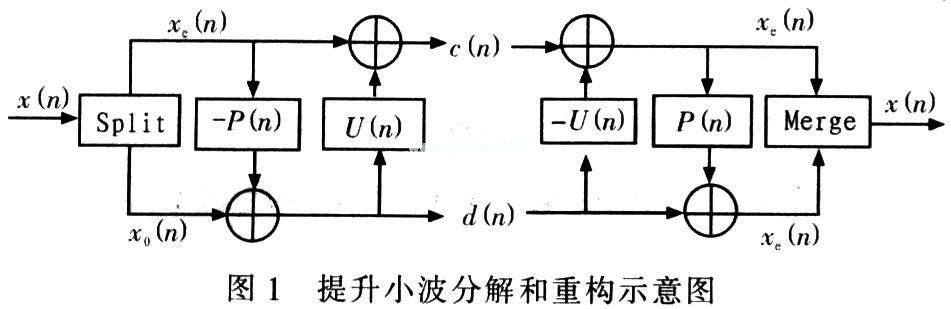
優點：速度是mallat分解的兩倍，可以實現原位運算（同址運算，不需要額外的儲存單元），可以實現整數小波變換，實現無失真壓縮。

JP2K裡的小波壓縮

Le Gall 5/3小波變換，用於無失真壓縮

分解是將資料分為偶數序列和奇數序列2個部分，預測是用分解的偶數序列預測奇數序列，得到的預測誤差為變換的高頻分量，更新是由預測誤差來更新偶數序列，得到變換的低頻分量。

Daubechies 9/7小波變換，用於有失真壓縮

雙正交小波基，具有線性相位，消失矩較大，能量集中性好等特性，在影象處理領域有廣泛的應用。影象經過9 /7小波分解後的低頻部分解析度高，高頻部分細節突出。

9 /7小波增加了一個預測和更新環節，可以防止影象重建誤差的擴大，提高系統穩定性，同時也保留了原位計算的特性，運算所需記憶體少，變換速度快。

5/3的分解與重構matlab實現：5/3分解與重構

Verilog程式碼通用性不強，就不上了。