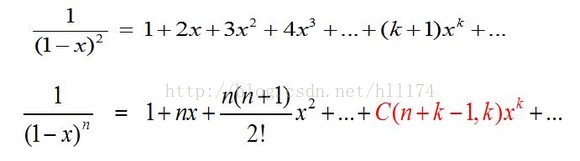介紹一下問題：

n個球放到m個盒子裡，則球和盒子是否有區別？是否允許空盒？

這自然有2³=8種狀態，用表格表示方案情況如下：

第一種情況的解釋：（n個無區別的球放進m個無區別的盒子中，允許空盒）

第二種情況的解釋：（n個無區別的球放進m個無區別的盒子中，不允許空盒）

將這兩種情況放在一起，這是因為這是同一個問題：正整數的拆分問題。所謂正整數的拆分問題指的是指把一個正整數拆分成若干正整數的和。不同的拆分法的數目稱為拆分數。

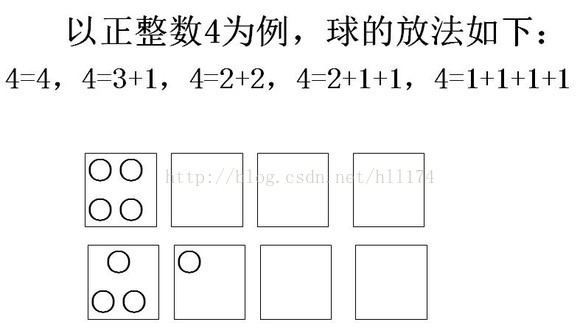
例如：考慮正整數4的拆分數：

4=4，4=3+1，4=2+2，4=2+1+1，4=1+1+1+1

正整數n的拆分，相當於把n個無區別的球放進m個無區別的盒子，盒子中允許放一個以上的球，也允許空著。依然以上面的4的拆分數為例子來說明：

上邊對應著4=4和4=3+1的兩種情況，其他的也類似，現在你已經同意這個觀點了“正整數n的拆分，相當於把n個無區別的球放進m個無區別的盒子，盒子中允許放一個以上的球，也允許空著。”好記住了它吧，凡是球無區別，盒子無區別，這一定是整數拆分問題。當然通過上面舉得例子你也會發現m>=n，畢竟最終有全是1的和的形式。

好了，有了上述我們達成的共識，下面我們繼續沒有完成的任務。

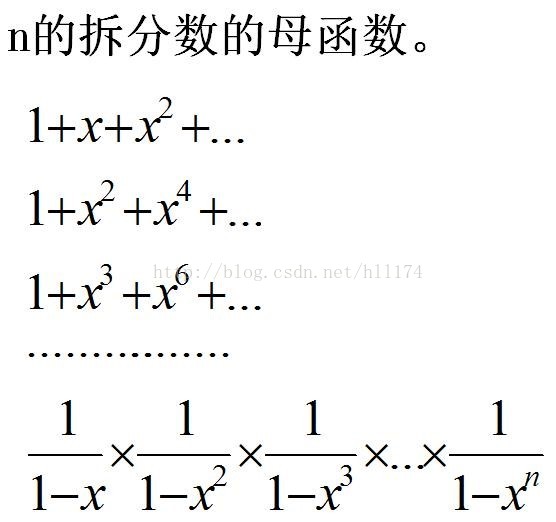
注：xn表示x的n次方，以下不再解釋。

上述公式中第一行是什麼意思呢，就是“1”表示拆分數中有0個1，“x”表示有1個1，“x2”表示有2個1，依此類推....

第二行什麼意思呢，就是“1”表示拆分數中有0個2，“x2”表示有1個2，“x4”表示有2個2，一次類推....

我相信第三行以及以下你一定知道什麼意思了。

通過無窮級數你肯定能得出最後一行的形式的，說白了就是一個無窮等比數列求和。最後一行中x的n次方的係數，就是我們要求的結果。有這麼神奇麼，還是用4的拆分數來驗證一下吧，自己算算x4的係數吧。

很神奇吧，好了言歸正傳吧。“n個無區別的球放進m個無區別的盒子中，（是否）允許空盒。”自然要用上面的理論來解決了。這裡我相信你能得出表格中我寫的原因解釋了。

我們繼續，看看第三種和第四種情況。

“n個無區別的球，放入m個有區別的盒子中，（是否）允許為空。”

我覺得原因解釋解釋的很清楚了，你需要的就是記住下面的公式：

公式怎麼推出來的，其實你學過的，給你個提示奧，去看看冪級數吧，再說的明白一點就是（1-x）分之一不斷的求導。

我們繼續看看5,6種情況。

“n個有區別的球，放入m個無區別的盒子中，（是否）允許為空。”

也就是表格中我用紅色標註的那兩行。

“n個有區別的球，放入m個無區別的盒子中，（是否）允許為空。”這個問題一定是允許重複的排列問題，也就是指數型母函式問題。

對原因解析中的內容做更加詳細的解釋；

“n個不同的元素,取m個作有重複的排列,與m個不同的球放進n個有區別的盒子,允許空盒的放法一一對應.”

上述這個例子，便可以說明問題了。所以看我寫的原因註釋吧，我相信你明白了。

終於，剩下兩種情況了，我們馬上就要解放了，好，加油了。

先來看看第二類斯特林數的定義：

“n個有區別的球放到m個相同的盒子中，要求無一空盒，其不同的方案數用S(n,m)表示，稱為第二類司特林數。”

“n個有區別的球，放入m個無區別的盒子中”，我們把盒子做一下全排列，會是什麼情況呢，你不覺得就是m個不同的盒子了麼。也就是“n個有區別的球，放入m個有區別的盒子中”的情況了麼？我假設你同意了，那S(n,m)怎麼求你也就會了，不是麼？哈哈，好好看看我寫的原因解釋吧。這裡不再羅嗦了。

最後我覺得我解決了所有的問題，現在寫的東西怎麼這種感覺呢。哎，怪就怪最近看Meyers的書看的吧，語氣就是跟他學的，你看這篇文章的時候沒有感覺到我再跟你對話麼？如果有，恭喜你，你已經掌握了。