深度學習激活函數們
如下圖，在神經元中，輸入的 inputs 通過加權，求和後，還被作用了一個函數，這個函數就是激活函數 Activation Function。
如果不用激勵函數，每一層輸出都是上層輸入的線性函數，無論神經網絡有多少層，輸出都是輸入的線性組合。
如果使用的話，激活函數給神經元引入了非線性因素，使得神經網絡可以任意逼近任何非線性函數，這樣神經網絡就可以應用到眾多的非線性模型中。
2. 常見的激活函數
(1) sigmoid函數
公式：
曲線：
導數：
sigmoid函數也叫 Logistic 函數，用於隱層神經元輸出，取值範圍為(0,1)，它可以將一個實數映射到(0,1)的區間，可以用來做二分類。
優點：
- 便於求導的平滑函數；
- 能壓縮數據，保證數據幅度不會有問題；
- 適合用於前向傳播。
缺點：
- 容易出現梯度消失（gradient vanishing）的現象：當激活函數接近飽和區時，變化太緩慢，導數接近0，根據後向傳遞的數學依據是微積分求導的鏈式法則，當前導數需要之前各層導數的乘積，幾個比較小的數相乘，導數結果很接近0，從而無法完成深層網絡的訓練。
- Sigmoid的輸出不是0均值（zero-centered）的：這會導致後層的神經元的輸入是非0均值的信號，這會對梯度產生影響。以 f=sigmoid(wx+b)為例， 假設輸入均為正數（或負數），那麽對w的導數總是正數（或負數），這樣在反向傳播過程中要麽都往正方向更新，要麽都往負方向更新，導致有一種捆綁效果，使得收斂緩慢。
- 冪運算，使得其相對耗時。
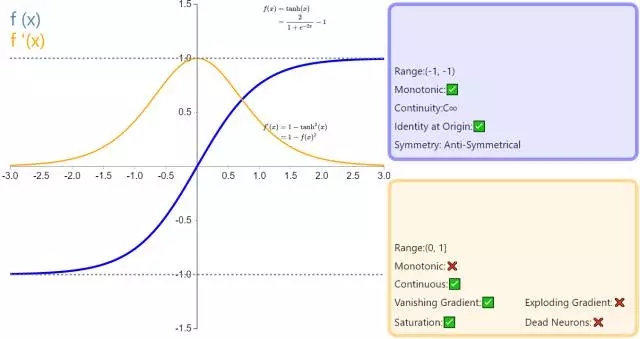
(2) Tanh函數（雙曲正切函數）
公式：
曲線：
導數：
tanh函數也稱為雙切正切函數，取值範圍為[-1,1]。
一個優點就是與 sigmoid 的區別是，tanh 是 0 均值的，因此實際應用中 tanh 會比 sigmoid 更好。
缺點類似sigmoid，雖然收斂速度相對快了，但也存在梯度彌散，而且也有冪計算，相對耗時。
(3) ReLU（線性修正單元）
公式：
曲線：
當輸入 x<0 時，輸出為 0，當 x> 0 時，輸出為 x。
優點：
（1）SGD算法的收斂速度比 sigmoid 和 tanh 快；（梯度不會飽和，解決了梯度消失問題）
（2）計算復雜度低，不需要進行指數運算；
（3）適合用於後向傳播。
缺點：
（1）ReLU的輸出不是zero-centered；
（2）Dead ReLU Problem（神經元壞死現象）：某些神經元可能永遠不會被激活，導致相應參數永遠不會被更新（在負數部分，梯度為0）。產生這種現象的兩個原因：參數初始化問題；learning rate太高導致在訓練過程中參數更新太大。 解決方法：采用Xavier初始化方法，以及避免將learning rate設置太大或使用adagrad等自動調節learning rate的算法。
（3）ReLU不會對數據做幅度壓縮，所以數據的幅度會隨著模型層數的增加不斷擴張。
(4) softmax函數
公式：
舉個例子來看公式的意思：
其求導往往結合交叉熵損失函數，具體見博客：https://www.cnblogs.com/CJT-blog/p/10419523.html
softmax主要用於多類分類。 softmax函數的輸出可用於表示所有類的概率分布，其中每個類的範圍為（0,1]，且其輸出滿足所有類概率和為1。
為什麽要取指數，第一個原因是要模擬 max 的行為，所以要讓大的更大。第二個原因是需要一個可導的函數。
3. 更多激活函數
下面是 26 個激活函數的圖示及其一階導數，圖的右側是一些與神經網絡相關的屬性。 1. Step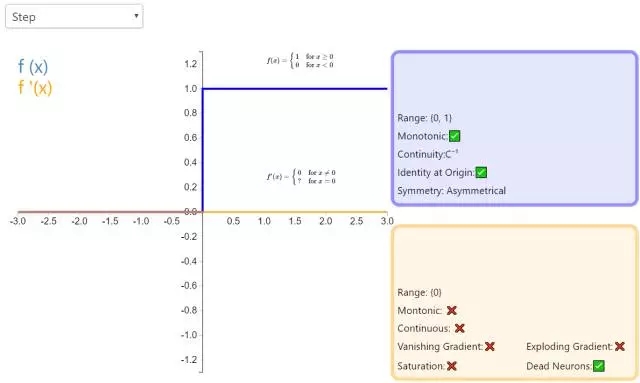
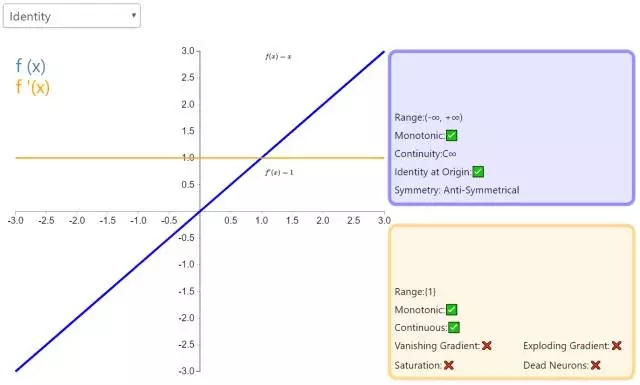
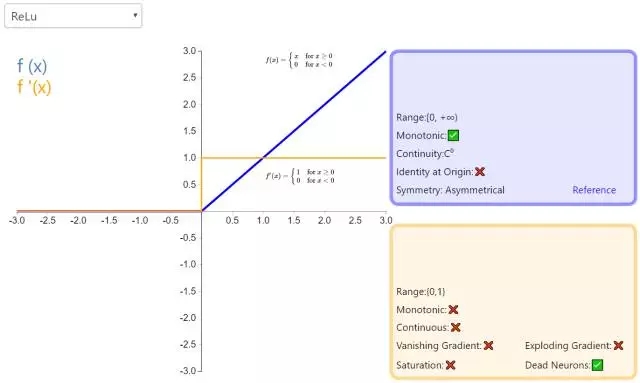
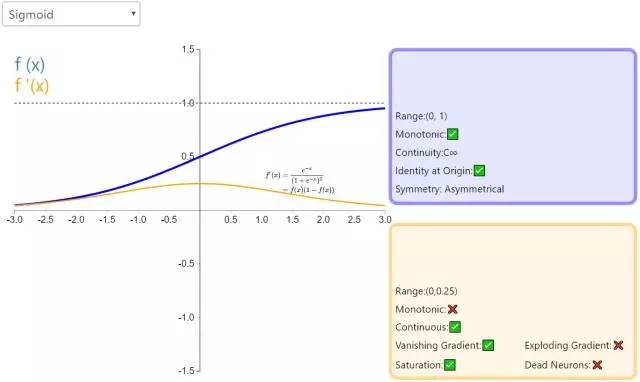
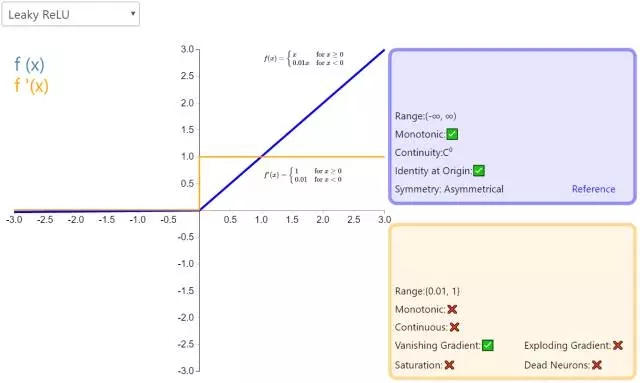
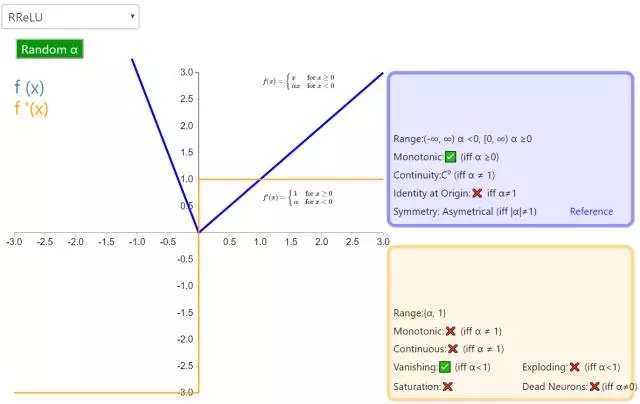
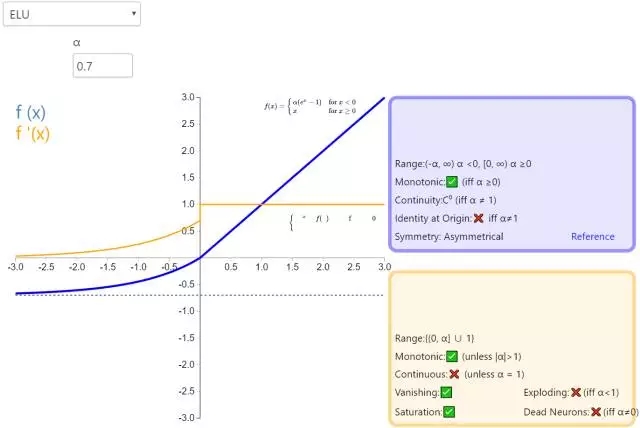
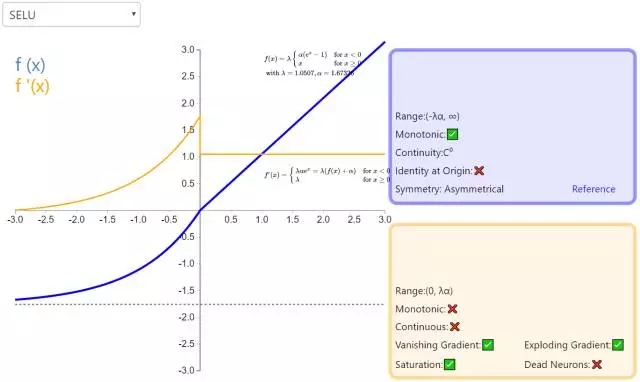
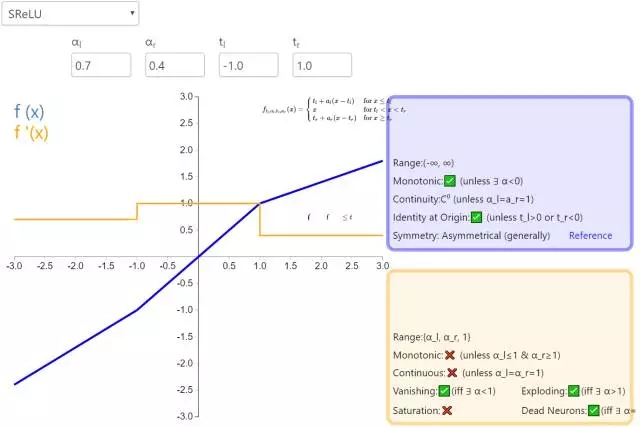
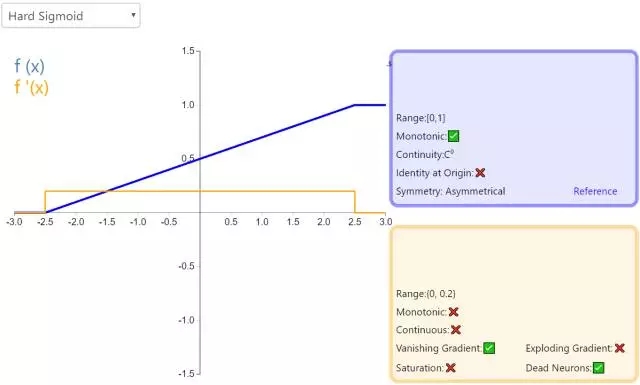
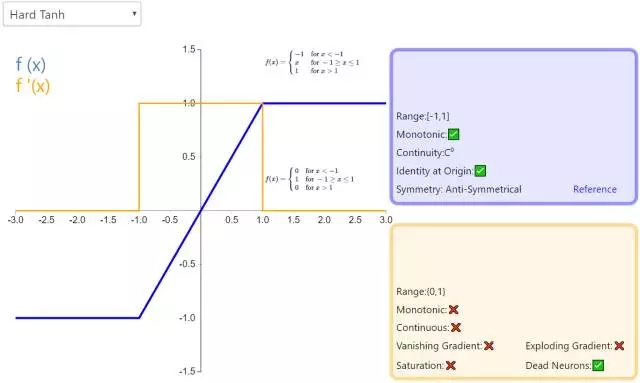
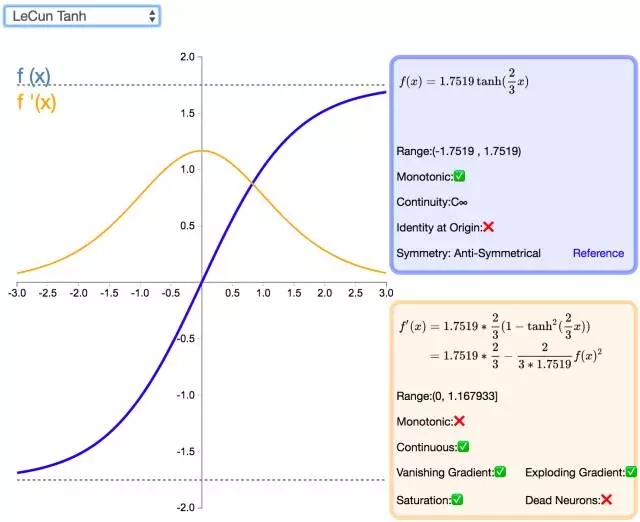
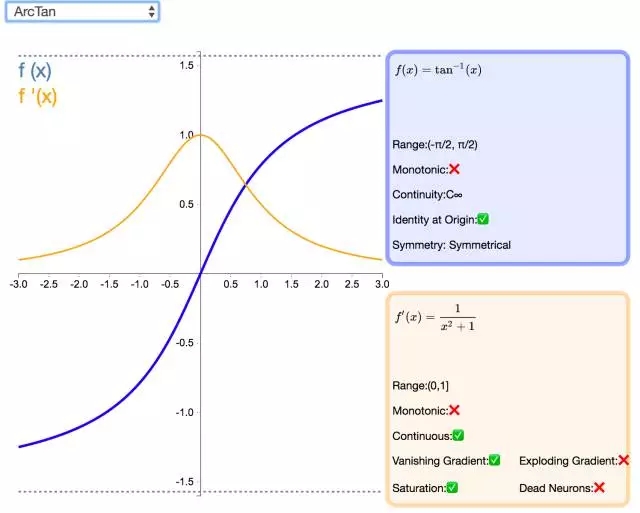
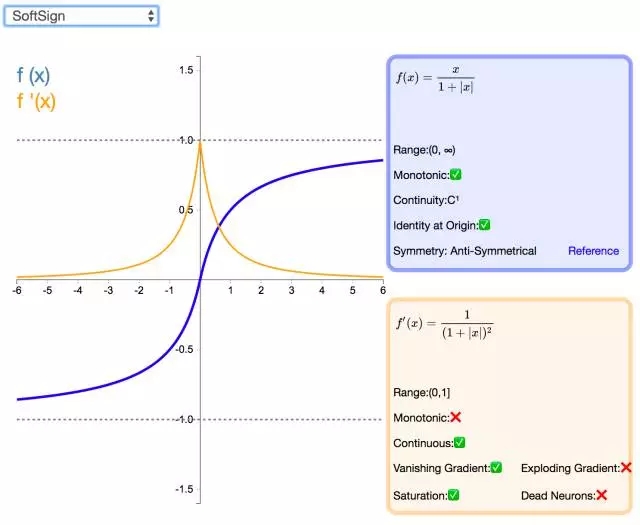
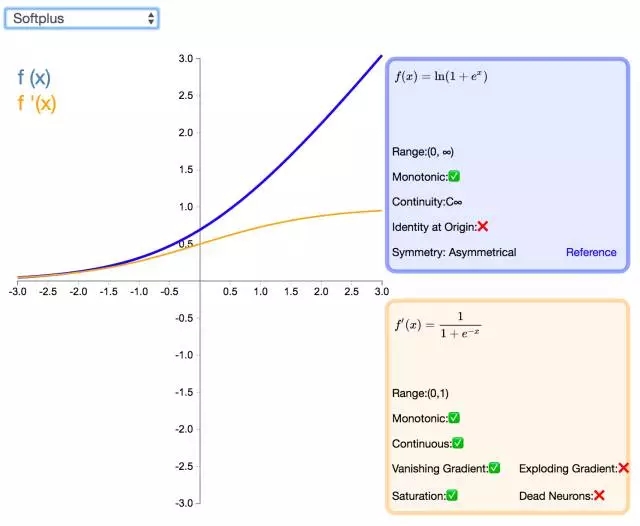
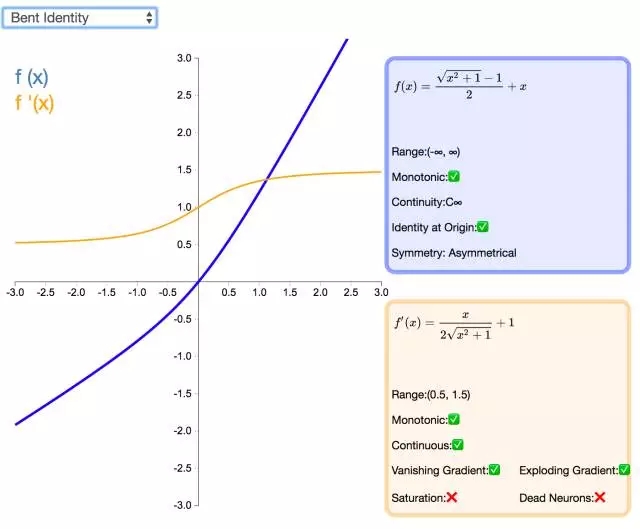
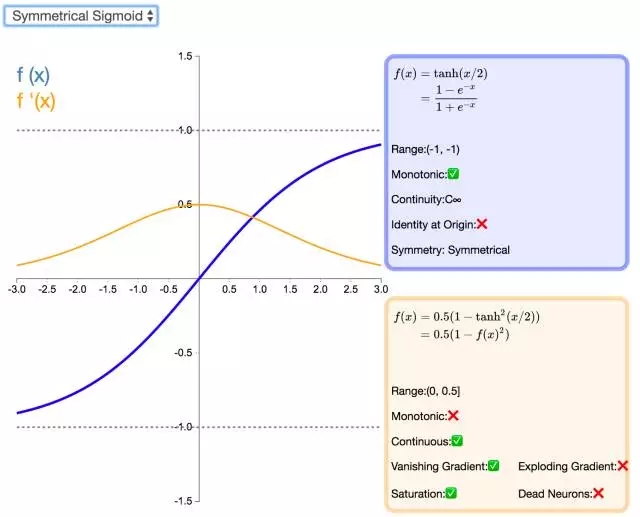
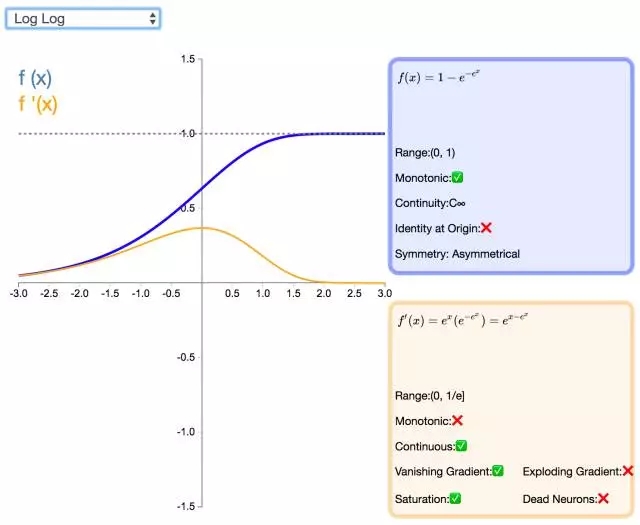
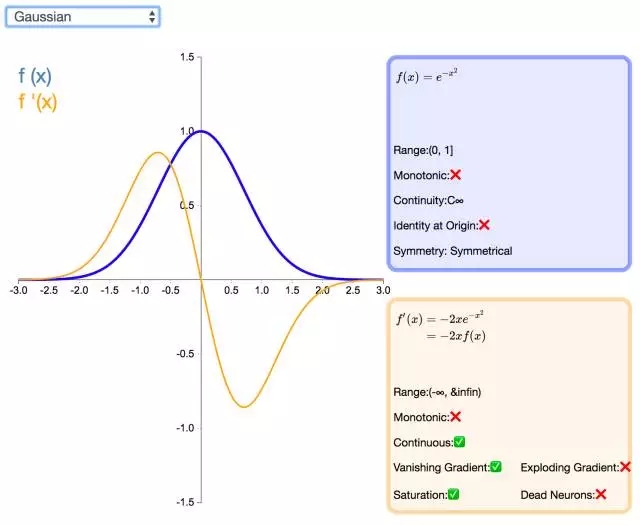
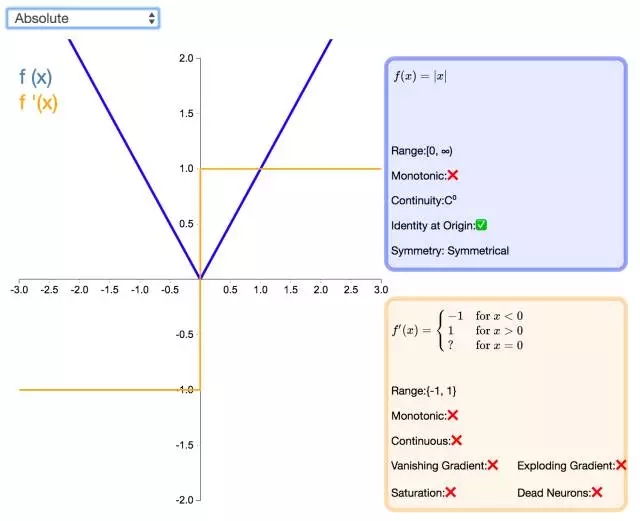
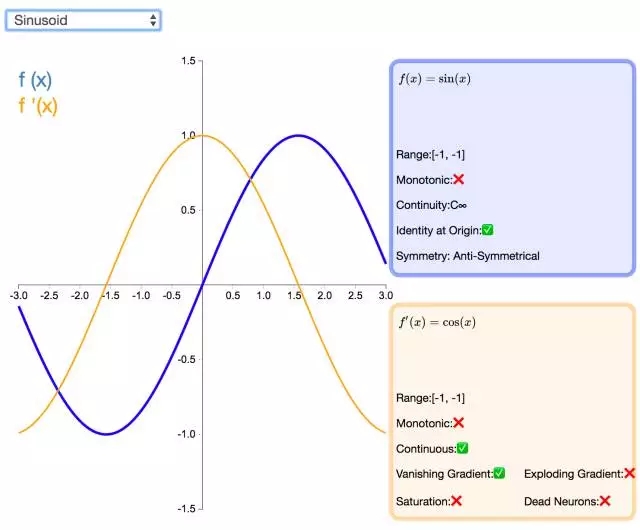
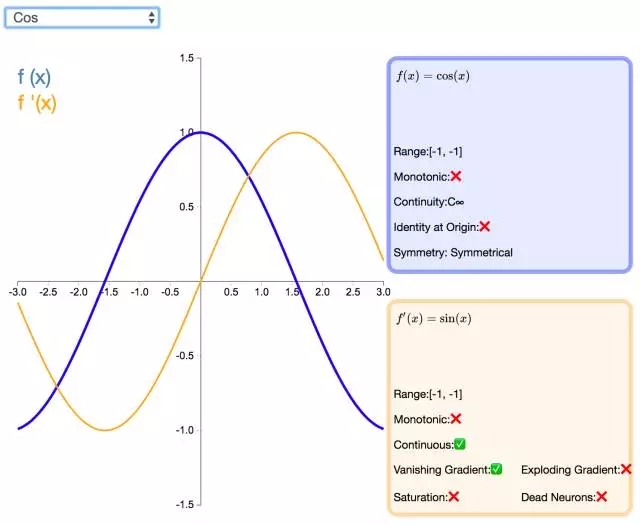
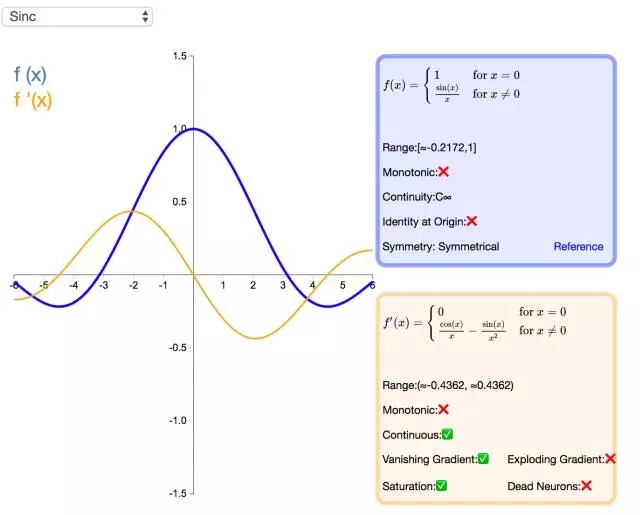
補充一個：maxout激活函數
參考:
https://www.cnblogs.com/lovychen/p/7561895.html
https://blog.csdn.net/qq_35200479/article/details/84502844
https://blog.csdn.net/not_guy/article/details/78749509
http://www.dataguru.cn/article-12255-1.html
https://www.cnblogs.com/makefile/p/activation-function.html
深度學習激活函數們