題意

題目描述

給定一棵\(n\)個點的樹，點帶點權。

有\(m\)次操作，每次操作給定\(x,y\)，表示修改點\(x\)的權值為\(y\)。

你需要在每次操作之後求出這棵樹的最大權獨立集的權值大小。

輸入輸出格式

輸入格式：

第一行，\(n,m\)，分別代表點數和操作數。

第二行，\(V_1,V_2,...,V_n\)，代表\(n\)個點的權值。

接下來\(n-1\)行，\(x,y\)，描述這棵樹的\(n-1\)條邊。

接下來\(m\)行，\(x,y\)，修改點\(x\)的權值為\(y\)。

輸出格式：

對於每個操作輸出一行一個整數，代表這次操作後的樹上最大權獨立集。

保證答案在int範圍內

輸入輸出樣例

輸入樣例#1：

10 10
-11 80 -99 -76 56 38 92 -51 -34 47
2 1
3 1
4 3
5 2
6 2
7 1
8 2
9 4
10 7
9 -44
2 -17
2 98
7 -58
8 48
3 99
8 -61
9 76
9 14
10 93

輸出樣例#1：

186
186
190
145
189
288
244
320
258
304

說明

對於30%的數據，\(1\le n,m\le 10\)
對於60%的數據，\(1\le n,m\le 1000\)
對於100%的數據，\(1\le n,m\le 10^5\)

分析

參照胡小兔的題解。

貓錕在WC2018講的黑科技——動態DP，就是一個畫風正常的DP問題再加上一個動態修改操作，就像這道題一樣。（這道題也是PPT中的例題）

動態DP的一個套路是把DP轉移方程寫成矩陣乘法，然後用線段樹（樹上的話就是樹剖）維護矩陣，這樣就可以做到修改了。

註意這個“矩陣乘法”不一定是我們常見的那種乘法和加法組成的矩陣乘法。設\(A?B=C\)，常見的那種矩陣乘法是這樣的：
\[ C_{i,j} = \sum_{k=1}^n A_{i,k}*B_{k,j} \]
而這道題中的矩陣乘法是這樣的：
\[ C_{i,j} = \max_{k=1}^n A_{i,k} + B_{k,j} \]
這就相當於常見矩陣乘法中的加法變成了max，乘法變成了加法。類似於乘法和加法的五種運算律，這兩種變化也滿足“加法交換律”、“加法結合律”、“max交換律”、“max結合律”和“加法分配律“。那麽這種矩陣乘法顯然也滿足矩陣乘法結合律，就像正常的矩陣乘法一樣，可以用線段樹維護。

接下來我們來構造矩陣。首先研究DP方程。

就像“沒有上司的舞會”一樣，\(f[i][0]\)表示子樹\(i\)中不選\(i\)的最大權獨立集大小，\(f[i][1]\)表示子樹\(i\)中選\(i\)的最大權獨立集大小。

但這是動態DP，我們需要加入動態維護的東西以支持修改操作。考慮樹鏈剖分。假設我們已經完成了樹鏈剖分，剖出來的某條重鏈看起來就像這樣，右邊的是在樹上深度較大的點：

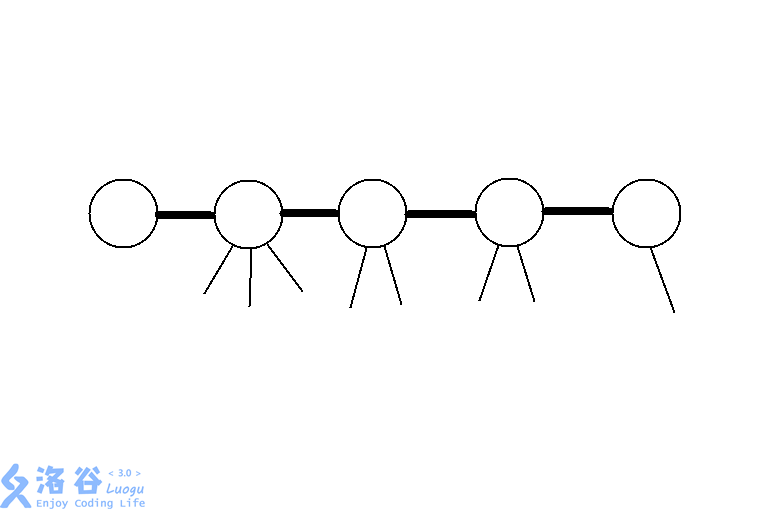
此時，比這條重鏈的top深度大且不在這條重鏈上的點的DP值都是已經求出來的（這可以做到）。我們把它們的貢獻，都統一於它們在這條重鏈上對應的那個祖先上。

具體來說，設\(g[i][0]\)表示不選i時，\(i\)不在鏈上的子孫的最大權獨立集大小，\(g[i][1]\)表示選\(i\)時，\(i\)不在鏈上的子孫再加上\(i\)自己的最大權獨立集大小。與一般的DP狀態的意義相比，除去了重兒子的貢獻，這是為了利用樹剖從任意節點到根最多\(\lceil \log_2 n \rceil\)條重鏈的性質，便於維護以後的修改操作。

假如\(i\)右面的點是\(i+1\), 那麽可以得出：
\[ f[i][0]=g[i][0]+\max\{f[i+1][0],f[i+1][1]\} \f[i][1]=g[i][1]+f[i+1][0] \]
矩陣也就可以構造出來了：
\[ \left( \begin{matrix} g[i][0] & g[i][0] \g[i][1] & 0 \end{matrix} \right) * \left( \begin{matrix} f[i+1][0] \\ f[i+1][1] \end{matrix} \right)= \left( \begin{matrix} f[i][0] \\ f[i][1] \end{matrix} \right) \]
讀者可以動筆驗證一下。（註意我們在這裏用的“新矩陣乘法”的規則：原來的乘變成加，加變成取max。）

那麽基本思路就很清楚了：樹剖，維護區間矩陣乘積，單個矩陣代表\(g\)，一條重鏈的矩陣乘積代表\(f\)。修改的時候，對於被修改節點到根節點路徑上的每個重鏈（由下到上），先單點修改\(g[i][1]\)，然後求出這條重鏈的\(top\)在修改之後的\(f\)值，然後更新\(fa[top]\)的\(g\)值，一直進行下去。

每次答案就是節點1的\(f\)值。

時間復雜度\(O(8n+8m\log^2 n)\)

代碼

用bfs實現了dfs1之後，直接用拓撲序實現了dfs2，非常巧妙，常數小。

#include<bits/stdc++.h>
#define rg register
#define il inline
#define co const
template<class T>il T read(){
    rg T data=0,w=1;
    rg char ch=getchar();
    while(!isdigit(ch)){
        if(ch=='-') w=-1;
        ch=getchar();
    }
    while(isdigit(ch))
        data=data*10+ch-'0',ch=getchar();
    return data*w;
}
template<class T>il T read(rg T&x){
    return x=read<T>();
}
typedef long long ll;
using namespace std;

co int N=1e5+5;
int n,m,a[N];
int ecnt,adj[N],nxt[2*N],go[2*N];
int fa[N],son[N],sze[N],top[N],idx[N],pos[N],tot,ed[N];
ll f[N][2];
struct matrix{
    ll g[2][2];
    matrix(){
        memset(g,0,sizeof g);
    }
    matrix operator*(co matrix&b)co{
        matrix c;
        for(int i=0;i<2;++i)
            for(int j=0;j<2;++j)
                for(int k=0;k<2;++k)
                    c.g[i][j]=max(c.g[i][j],g[i][k]+b.g[k][j]);
        return c;
    }
}val[N],data[4*N];

void add(int u,int v){
    go[++ecnt]=v,nxt[ecnt]=adj[u],adj[u]=ecnt;
}
void init(){
    static int que[N];
    que[1]=1;
    for(int ql=1,qr=1;ql<=qr;++ql)
        for(int u=que[ql],e=adj[u],v;e;e=nxt[e])
            if((v=go[e])!=fa[u])
                fa[v]=u,que[++qr]=v;
    for(int qr=n,u;qr;--qr){
        sze[u=que[qr]]++;
        sze[fa[u]]+=sze[u];
        if(sze[u]>sze[son[fa[u]]]) son[fa[u]]=u;
    }
    for(int ql=1,u;ql<=n;++ql)
        if(!top[u=que[ql]]){
            for(int v=u;v;v=son[v])
                top[v]=u,idx[pos[v]=++tot]=v;
            ed[u]=tot;
        }
    for(int qr=n,u;qr;--qr){
        u=que[qr];
        f[u][1]=max(0,a[u]);
        for(int e=adj[u],v;e;e=nxt[e])
            if(v=go[e],v!=fa[u]){
                f[u][0]+=max(f[v][0],f[v][1]);
                f[u][1]+=f[v][0];
            }
    }
}

void build(int k,int l,int r){
    if(l==r){
        ll g0=0,g1=a[idx[l]];
        for(int u=idx[l],e=adj[u],v;e;e=nxt[e])
            if((v=go[e])!=fa[u]&&v!=son[u])
                g0+=max(f[v][0],f[v][1]),g1+=f[v][0];
        data[k].g[0][0]=data[k].g[0][1]=g0;
        data[k].g[1][0]=g1;
        val[l]=data[k];
        return;
    }
    int mid=l+r>>1;
    build(k<<1,l,mid);
    build(k<<1|1,mid+1,r);
    data[k]=data[k<<1]*data[k<<1|1];
}
void change(int k,int l,int r,int p){
    if(l==r){
        data[k]=val[l];
        return;
    }
    int mid=l+r>>1;
    if(p<=mid) change(k<<1,l,mid,p);
    else change(k<<1|1,mid+1,r,p);
    data[k]=data[k<<1]*data[k<<1|1];
}
matrix query(int k,int l,int r,int ql,int qr){
    if(ql<=l&&r<=qr) return data[k];
    int mid=l+r>>1;
    if(qr<=mid) return query(k<<1,l,mid,ql,qr);
    if(ql>mid) return query(k<<1|1,mid+1,r,ql,qr);
    return query(k<<1,l,mid,ql,qr)*query(k<<1|1,mid+1,r,ql,qr);
}
matrix ask(int u){
    return query(1,1,n,pos[top[u]],ed[top[u]]);
}
void path_change(int u,int x){
    val[pos[u]].g[1][0]+=x-a[u];
    a[u]=x;
    matrix od,nw;
    while(u){
        od=ask(top[u]);
        change(1,1,n,pos[u]);
        nw=ask(top[u]);
        u=fa[top[u]];
        val[pos[u]].g[0][0]+=max(nw.g[0][0],nw.g[1][0])-max(od.g[0][0],od.g[1][0]);
        val[pos[u]].g[0][1]=val[pos[u]].g[0][0];
        val[pos[u]].g[1][0]+=nw.g[0][0]-od.g[0][0];
    }
}
int main(){
//  freopen(".in","r",stdin);
//  freopen(".out","w",stdout);
    read(n),read(m);
    for(int i=1;i<=n;++i) read(a[i]);
    for(int i=1,u,v;i<n;++i)
        read(u),read(v),add(u,v),add(v,u);
    init();
    build(1,1,n);
    int u,x;
    matrix t;
    while(m--){
        read(u),read(x);
        path_change(u,x);
        t=ask(1);
        printf("%lld\n",max(t.g[0][0],t.g[1][0]));
    }
    return 0;
}

LG4719 【模板】動態dp